Ułamki Zwykłe Rozszerzanie I Skracanie

Witaj! Dziś zajmiemy się ułamkami zwykłymi i dwiema bardzo ważnymi operacjami, które możemy na nich wykonywać: rozszerzaniem i skracaniem. To kluczowe umiejętności, które pomogą Ci lepiej zrozumieć ułamki i wykonywać na nich różne działania.
Czym jest ułamek zwykły?
Zanim przejdziemy do rozszerzania i skracania, przypomnijmy sobie, co to w ogóle jest ułamek zwykły. Ułamek zwykły to po prostu sposób na zapisanie liczby, która reprezentuje część całości. Składa się z dwóch liczb oddzielonych kreską ułamkową:
- Licznik: liczba znajdująca się nad kreską ułamkową. Mówi nam, ile części całości bierzemy.
- Mianownik: liczba znajdująca się pod kreską ułamkową. Mówi nam, na ile równych części podzielona jest całość.
Na przykład, ułamek 3/4 oznacza, że podzieliliśmy coś na 4 równe części i bierzemy z tego 3 części. Możemy to sobie wyobrazić jako pizzę podzieloną na 4 kawałki, z których zjemy 3.
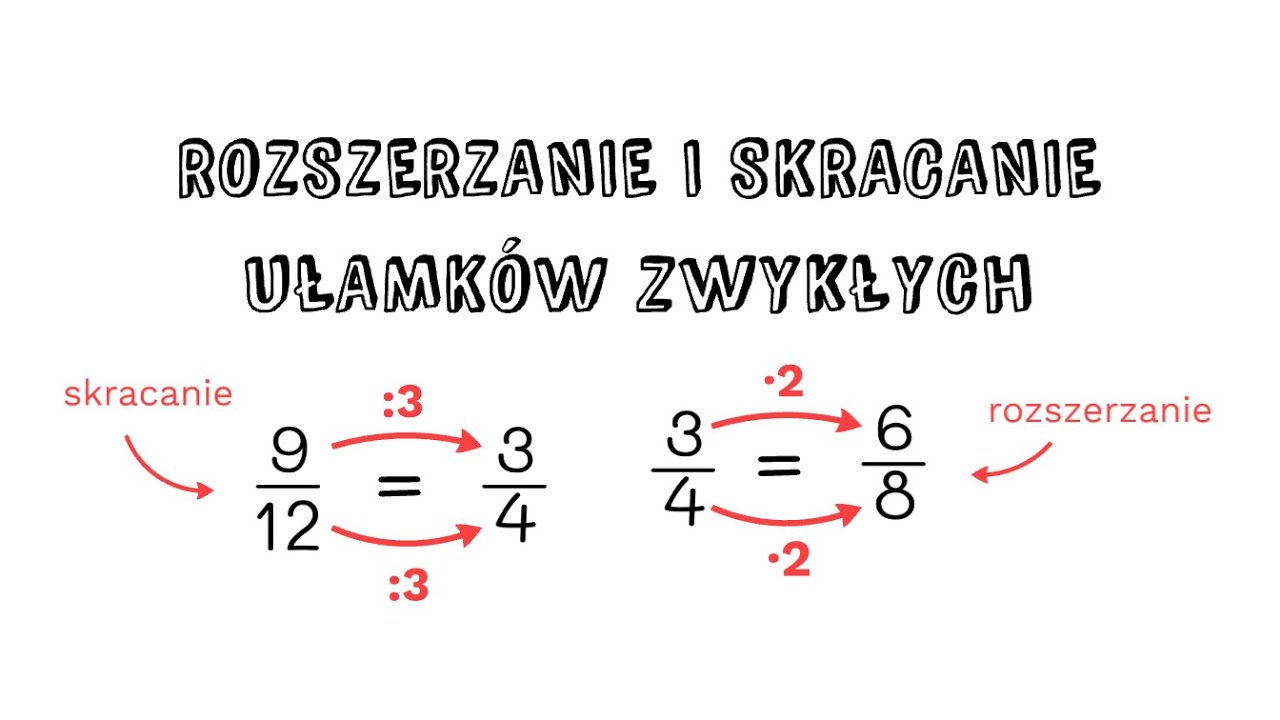
Rozszerzanie ułamków
Rozszerzanie ułamka polega na pomnożeniu zarówno licznika, jak i mianownika przez tę samą liczbę różną od zera. Brzmi skomplikowanie? Spokojnie, zaraz to wszystko wyjaśnimy.
Dlaczego to robimy? Rozszerzanie ułamka pozwala nam zmienić jego wygląd, ale nie zmienia jego wartości. To tak, jakbyśmy kroili pizzę na więcej kawałków, ale w sumie zjedli dokładnie tyle samo pizzy.
Jak rozszerzyć ułamek?
Załóżmy, że mamy ułamek 1/2 i chcemy go rozszerzyć przez 3. Robimy to tak:
- Mnożymy licznik (1) przez 3: 1 * 3 = 3
- Mnożymy mianownik (2) przez 3: 2 * 3 = 6
W ten sposób otrzymujemy ułamek 3/6. Ułamki 1/2 i 3/6 są równe, czyli mają tę samą wartość. Możemy to sprawdzić, wyobrażając sobie pół pizzy i trzy kawałki z sześciokrotnie pokrojonej pizzy. To jest dokładnie to samo!
Przykład
Rozszerzmy ułamek 2/5 przez 4:
- Licznik: 2 * 4 = 8
- Mianownik: 5 * 4 = 20
Otrzymujemy ułamek 8/20. Zatem 2/5 = 8/20.
Dlaczego rozszerzamy ułamki?
Rozszerzanie ułamków jest bardzo przydatne, gdy chcemy porównać ułamki o różnych mianownikach lub gdy chcemy je dodać lub odjąć. Na przykład, aby porównać ułamki 1/3 i 1/4, możemy je rozszerzyć tak, aby miały ten sam mianownik. Możemy oba rozszerzyć do mianownika 12: 1/3 = 4/12 i 1/4 = 3/12. Teraz łatwo widzimy, że 1/3 jest większe niż 1/4.
Skracanie ułamków
Skracanie ułamka jest operacją odwrotną do rozszerzania. Polega na podzieleniu zarówno licznika, jak i mianownika przez tę samą liczbę różną od zera, która jest ich wspólnym dzielnikiem. Podobnie jak rozszerzanie, skracanie nie zmienia wartości ułamka.
Celem skracania jest uproszczenie ułamka, czyli zapisanie go w postaci, w której licznik i mianownik są jak najmniejsze.
Jak skrócić ułamek?
Załóżmy, że mamy ułamek 6/8 i chcemy go skrócić. Szukamy liczby, która dzieli zarówno 6, jak i 8. Zauważamy, że obie liczby są podzielne przez 2.
- Dzielimy licznik (6) przez 2: 6 / 2 = 3
- Dzielimy mianownik (8) przez 2: 8 / 2 = 4
W ten sposób otrzymujemy ułamek 3/4. Ułamki 6/8 i 3/4 są równe. Ułamek 3/4 jest postacią nieskracalną ułamka 6/8, co oznacza, że nie możemy go już bardziej uprościć.
Przykład
Skróćmy ułamek 12/18. Obie liczby są podzielne przez 2, więc możemy zacząć od tego:
- Licznik: 12 / 2 = 6
- Mianownik: 18 / 2 = 9
Otrzymujemy ułamek 6/9. Ale zauważamy, że 6 i 9 nadal mają wspólny dzielnik, którym jest 3. Dzielimy więc dalej:
- Licznik: 6 / 3 = 2
- Mianownik: 9 / 3 = 3
Otrzymujemy ułamek 2/3. To jest postać nieskracalna ułamka 12/18.
Znajdowanie największego wspólnego dzielnika (NWD)
Aby skrócić ułamek jak najszybciej, warto znaleźć największy wspólny dzielnik (NWD) licznika i mianownika. Na przykład, w przypadku ułamka 12/18, NWD liczb 12 i 18 to 6. Gdybyśmy od razu podzielili licznik i mianownik przez 6, otrzymalibyśmy od razu ułamek 2/3.
Dlaczego skracamy ułamki?
Skracanie ułamków ułatwia nam pracę z nimi. Uproszczone ułamki są łatwiejsze do porównywania, dodawania, odejmowania, mnożenia i dzielenia. Poza tym, wynik obliczeń zazwyczaj przedstawia się w postaci nieskracalnej.
Podsumowanie
Rozszerzanie i skracanie ułamków to bardzo ważne umiejętności. Pamiętaj, że obie te operacje nie zmieniają wartości ułamka, a jedynie jego wygląd. Rozszerzanie polega na pomnożeniu licznika i mianownika przez tę samą liczbę, a skracanie na podzieleniu licznika i mianownika przez ich wspólny dzielnik. Ćwicz regularnie, a szybko opanujesz te umiejętności!