Ułamki Zwykłe Przykłady Klasa 5

Witaj w świecie ułamków zwykłych! Ten artykuł został przygotowany specjalnie dla uczniów klasy 5, aby pomóc zrozumieć, czym są ułamki zwykłe, jak się nimi posługiwać i gdzie możemy je spotkać w życiu codziennym. Ułamki mogą wydawać się na początku skomplikowane, ale z odpowiednim wyjaśnieniem i praktyką staną się proste i intuicyjne.

Co to jest ułamek zwykły?

Ułamek zwykły to sposób zapisu liczby, która reprezentuje część całości. Wyobraź sobie pizzę podzieloną na równe kawałki. Ułamek pomoże Ci opisać, ile kawałków tej pizzy masz. Składa się z dwóch ważnych elementów: licznika i mianownika. Są one oddzielone od siebie kreską ułamkową.

Licznik (liczba nad kreską ułamkową) mówi nam, ile części bierzemy pod uwagę. Na przykład, jeśli masz 3 kawałki pizzy, licznik będzie wynosił 3.

Mianownik (liczba pod kreską ułamkową) informuje nas, na ile równych części podzielona jest całość. Jeżeli pizza była podzielona na 8 kawałków, mianownik wyniesie 8.

Zatem, jeśli masz 3 kawałki pizzy podzielonej na 8 kawałków, zapiszemy to jako ułamek 3/8 (czytamy "trzy ósme").

Przykłady ułamków zwykłych:

• 1/2 (jedna druga) – połowa czegoś
• 1/4 (jedna czwarta) – ćwierć czegoś
• 2/3 (dwie trzecie)
• 5/6 (pięć szóstych)
• 7/10 (siedem dziesiątych)

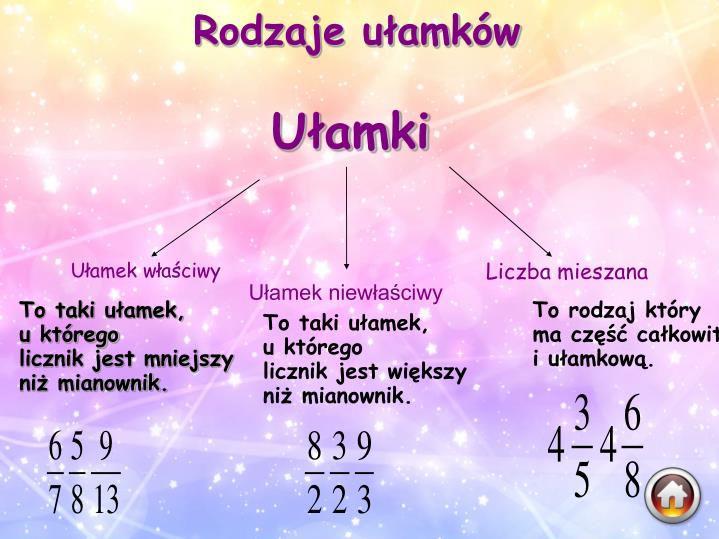
Rodzaje ułamków zwykłych

Ułamki zwykłe możemy podzielić na kilka kategorii, w zależności od relacji między licznikiem a mianownikiem:

Ułamki właściwe

Ułamek właściwy to taki ułamek, w którym licznik jest mniejszy od mianownika. Oznacza to, że ułamek reprezentuje mniej niż jedną całość. Przykłady:

• 1/2
• 3/4
• 5/8
• 9/10

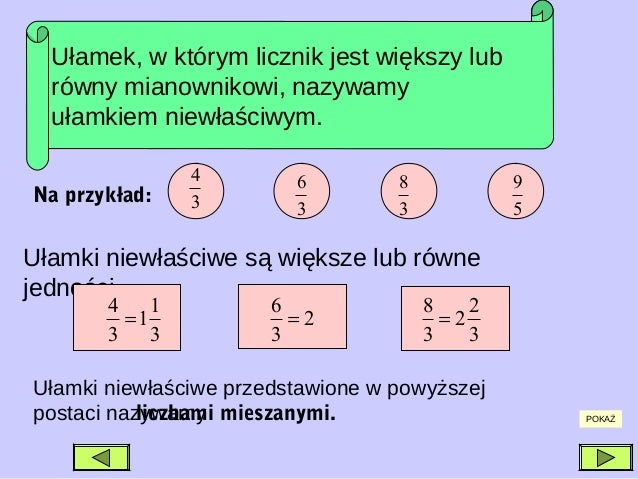
Ułamki niewłaściwe

Ułamek niewłaściwy to taki ułamek, w którym licznik jest większy lub równy mianownikowi. Oznacza to, że ułamek reprezentuje jedną całość lub więcej niż jedną całość. Przykłady:

• 4/4 (równa się 1)
• 5/4 (więcej niż 1)
• 7/2 (więcej niż 3)
• 10/3 (więcej niż 3)

Liczby mieszane

Liczba mieszana to sposób zapisu ułamka niewłaściwego, który składa się z liczby całkowitej i ułamka właściwego. Na przykład, ułamek 5/4 możemy zapisać jako liczbę mieszaną 1 1/4 (czytamy "jeden i jedna czwarta"). Oznacza to, że mamy jedną całą jednostkę i jeszcze jedną czwartą tej jednostki.

Zamiana ułamka niewłaściwego na liczbę mieszaną:

Aby zamienić ułamek niewłaściwy na liczbę mieszaną, dzielimy licznik przez mianownik. Wynik dzielenia (część całkowita) to liczba całkowita w liczbie mieszanej. Reszta z dzielenia to licznik ułamka właściwego, a mianownik pozostaje bez zmian.

Przykład: 7/3. Dzielimy 7 przez 3. Wynik to 2 (liczba całkowita), a reszta to 1. Zatem 7/3 = 2 1/3.

Zamiana liczby mieszanej na ułamek niewłaściwy:

Aby zamienić liczbę mieszaną na ułamek niewłaściwy, mnożymy liczbę całkowitą przez mianownik ułamka właściwego, dodajemy licznik ułamka właściwego, a wynik zapisujemy jako licznik ułamka niewłaściwego. Mianownik pozostaje bez zmian.

Przykład: 2 1/3. Mnożymy 2 przez 3 (wynik to 6), dodajemy 1 (wynik to 7). Zatem 2 1/3 = 7/3.

Rozszerzanie i skracanie ułamków

Rozszerzanie ułamków polega na pomnożeniu licznika i mianownika przez tę samą liczbę różną od zera. W ten sposób otrzymujemy ułamek równy danemu ułamkowi, ale z większymi liczbami w liczniku i mianowniku.

Przykład: Rozszerzamy ułamek 1/2 przez 3. Mnożymy licznik (1) przez 3, co daje 3. Mnożymy mianownik (2) przez 3, co daje 6. Zatem 1/2 = 3/6.

Skracanie ułamków polega na podzieleniu licznika i mianownika przez tę samą liczbę różną od zera. W ten sposób otrzymujemy ułamek równy danemu ułamkowi, ale z mniejszymi liczbami w liczniku i mianowniku.

Przykład: Skracamy ułamek 6/8 przez 2. Dzielimy licznik (6) przez 2, co daje 3. Dzielimy mianownik (8) przez 2, co daje 4. Zatem 6/8 = 3/4.

Ułamek nieskracalny to taki ułamek, którego nie można już skrócić, czyli licznik i mianownik nie mają wspólnego dzielnika większego od 1.

Porównywanie ułamków

Porównywanie ułamków pozwala nam określić, który ułamek jest większy, mniejszy lub czy ułamki są równe.

Ułamki o tych samych mianownikach

Jeśli ułamki mają ten sam mianownik, to większy jest ten ułamek, który ma większy licznik.

Przykład: Porównaj 3/5 i 1/5. Mianowniki są takie same (5). Licznik 3 jest większy od licznika 1. Zatem 3/5 > 1/5.

Ułamki o różnych mianownikach

Jeśli ułamki mają różne mianowniki, musimy sprowadzić je do wspólnego mianownika, a następnie porównać liczniki. Najczęściej szukamy najmniejszej wspólnej wielokrotności (NWW) mianowników, aby uzyskać najmniejszy wspólny mianownik.

Przykład: Porównaj 1/2 i 1/3. Mianowniki to 2 i 3. NWW(2, 3) = 6. Sprowadzamy ułamki do wspólnego mianownika 6:

• 1/2 = (1 * 3) / (2 * 3) = 3/6
• 1/3 = (1 * 2) / (3 * 2) = 2/6

Teraz możemy porównać 3/6 i 2/6. Licznik 3 jest większy od licznika 2. Zatem 3/6 > 2/6, co oznacza, że 1/2 > 1/3.

Działania na ułamkach zwykłych

Nauka wykonywania działań na ułamkach to kluczowa umiejętność. Omówimy dodawanie, odejmowanie, mnożenie i dzielenie.

Dodawanie ułamków

Aby dodać ułamki o tych samych mianownikach, dodajemy liczniki, a mianownik pozostaje bez zmian.

Przykład: 2/5 + 1/5 = (2 + 1) / 5 = 3/5.

Aby dodać ułamki o różnych mianownikach, musimy najpierw sprowadzić je do wspólnego mianownika, a następnie dodać liczniki.

Przykład: 1/2 + 1/3. NWW(2, 3) = 6. Sprowadzamy ułamki do wspólnego mianownika:

• 1/2 = 3/6
• 1/3 = 2/6

Teraz możemy dodać: 3/6 + 2/6 = (3 + 2) / 6 = 5/6.

Odejmowanie ułamków

Aby odjąć ułamki o tych samych mianownikach, odejmujemy liczniki, a mianownik pozostaje bez zmian.

Przykład: 3/4 - 1/4 = (3 - 1) / 4 = 2/4. Możemy skrócić 2/4 do 1/2.

Aby odjąć ułamki o różnych mianownikach, musimy najpierw sprowadzić je do wspólnego mianownika, a następnie odjąć liczniki.

Przykład: 1/2 - 1/3. NWW(2, 3) = 6. Sprowadzamy ułamki do wspólnego mianownika:

• 1/2 = 3/6
• 1/3 = 2/6

Teraz możemy odjąć: 3/6 - 2/6 = (3 - 2) / 6 = 1/6.

Mnożenie ułamków

Aby pomnożyć ułamki, mnożymy licznik przez licznik i mianownik przez mianownik.

Przykład: 1/2 * 2/3 = (1 * 2) / (2 * 3) = 2/6. Możemy skrócić 2/6 do 1/3.

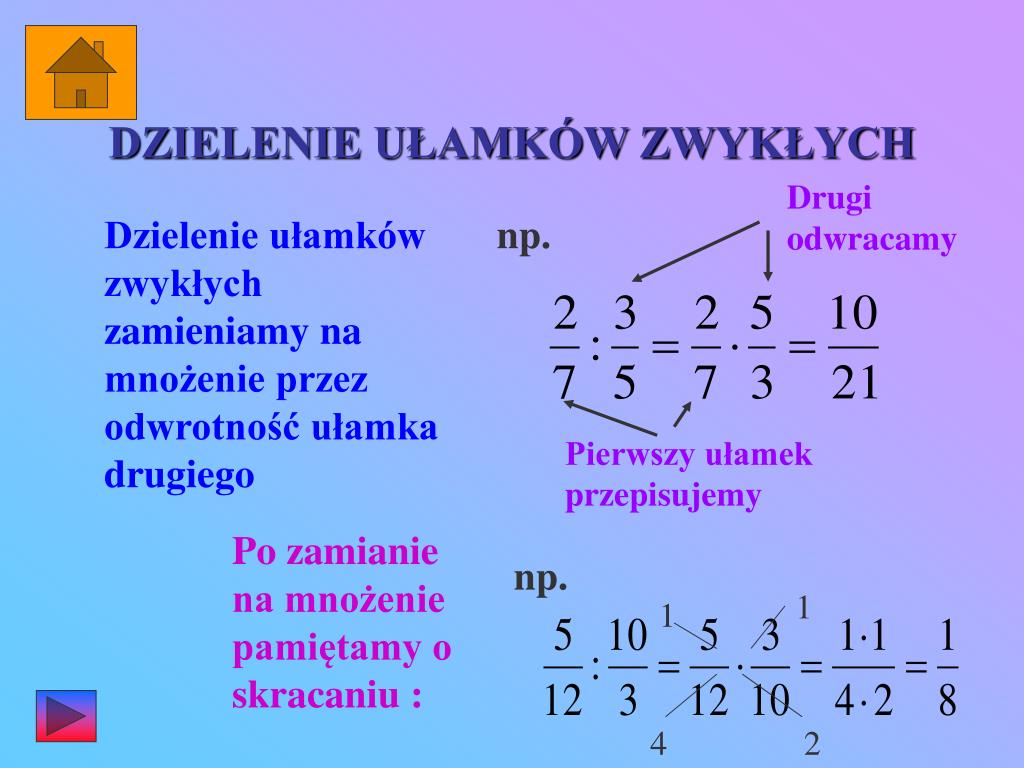
Dzielenie ułamków

Aby podzielić ułamki, mnożymy pierwszy ułamek przez odwrotność drugiego ułamka. Odwrotność ułamka to ułamek, w którym zamieniliśmy licznik z mianownikiem.

Przykład: 1/2 : 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4.

Ułamki w życiu codziennym

Ułamki są obecne w wielu aspektach naszego życia, często nawet o tym nie myślimy!

• Gotowanie: Przepisy kulinarne często podają ilości składników w ułamkach, np. 1/2 szklanki mąki, 1/4 łyżeczki soli.
• Mierzenie: Używamy ułamków do mierzenia długości (np. 1/2 metra materiału), wagi (np. 1/4 kilograma sera) i czasu (np. 1/2 godziny).
• Podział: Dzielimy się z innymi, używając ułamków. Na przykład, dzielimy pizzę na 8 kawałków i każdy z nas dostaje 2/8 (czyli 1/4) pizzy.
• Zakupy: Często spotykamy promocje w sklepach, które wyrażone są ułamkami, np. "Kup 2, a trzeci produkt 1/2 ceny".
• Sport: W sporcie ułamki mogą reprezentować czas, np. 1/10 sekundy szybszy czas na okrążeniu.

Przykład z życia wzięty: Wyobraź sobie, że pieczesz ciasto. Przepis wymaga 3/4 szklanki cukru. Masz tylko miarkę o pojemności 1/4 szklanki. Ile razy musisz napełnić tę miarkę, aby odmierzyć potrzebną ilość cukru? Odpowiedź to 3, ponieważ 3 * (1/4) = 3/4.

Podsumowanie

Ułamki zwykłe to fundamentalne narzędzie w matematyce, które pomaga nam rozumieć i opisywać części całości. Zrozumienie licznika, mianownika, różnych rodzajów ułamków, rozszerzania i skracania ułamków oraz wykonywania działań na ułamkach jest kluczowe dla dalszej nauki matematyki. Pamiętaj, że praktyka czyni mistrza! Rozwiązuj zadania, szukaj ułamków w swoim otoczeniu i baw się matematyką! Nie bój się zadawać pytań, jeśli coś jest niejasne. Powodzenia!

Zadanie dla Ciebie: Spróbuj znaleźć 5 przykładów użycia ułamków w swoim życiu codziennym. Zapisz je i podziel się nimi z kolegami i koleżankami z klasy. Powodzenia!