Ułamki Zwykłe Mnożenie I Dzielenie
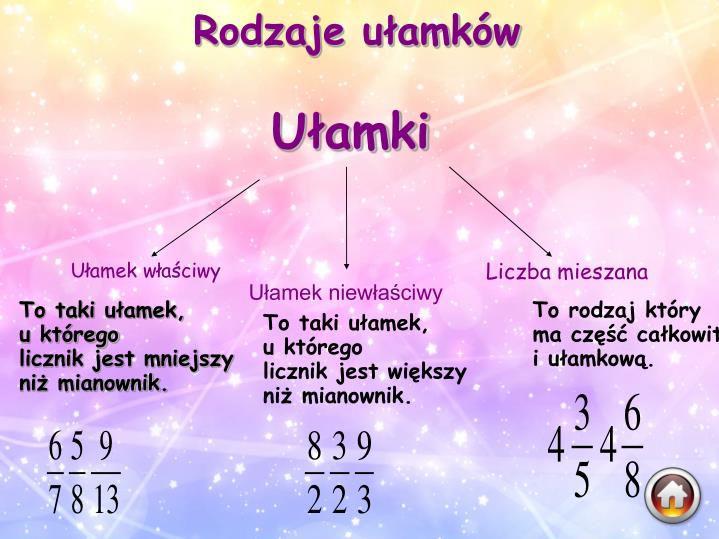
W świecie matematyki, ułamki zwykłe stanowią fundament wielu operacji i obliczeń. Zrozumienie, jak je mnożyć i dzielić, jest kluczowe nie tylko dla sukcesu w szkole, ale również dla zastosowań praktycznych w życiu codziennym. Niniejszy artykuł ma na celu dogłębne wyjaśnienie tych operacji, od podstawowych zasad po bardziej złożone przykłady.
Mnożenie Ułamków Zwykłych
Zasady Mnożenia
Mnożenie ułamków zwykłych jest relatywnie proste. Mnożymy licznik przez licznik, a mianownik przez mianownik. Otrzymany wynik to nowy ułamek, którego licznik jest wynikiem mnożenia liczników, a mianownik wynikiem mnożenia mianowników. To proste!
Formalnie, jeśli mamy dwa ułamki a/b oraz c/d, ich iloczyn wynosi:
a/b * c/d = a*c/b*d
Na przykład:
1/2 * 2/3 = 1*2/2*3 = 2/6
Następnie, ułamek 2/6 możemy uprościć do 1/3.
Upraszczanie Ułamków Przed Mnożeniem
Upraszczanie ułamków przed mnożeniem może znacznie ułatwić obliczenia, zwłaszcza przy większych liczbach. Polega to na znalezieniu wspólnych czynników w licznikach i mianownikach i skróceniu ich przed wykonaniem mnożenia. Szukaj czynników!
Rozważmy przykład:
6/8 * 4/9
Zamiast mnożyć od razu 6*4 i 8*9, możemy zauważyć, że 6 i 9 mają wspólny czynnik 3, a 4 i 8 mają wspólny czynnik 4. Dzielimy więc 6 przez 3, co daje 2, i 9 przez 3, co daje 3. Podobnie dzielimy 4 przez 4, co daje 1, i 8 przez 4, co daje 2. Wtedy mamy:
2/2 * 1/3 = 1/1 * 1/3 = 2/6 = 1/3
Zauważmy, że otrzymaliśmy ten sam wynik, ale uniknęliśmy operowania na większych liczbach.
Mnożenie Ułamków przez Liczby Całkowite
Mnożenie ułamka przez liczbę całkowitą jest równoważne mnożeniu ułamka przez ułamek, w którym liczba całkowita jest licznikiem, a mianownik wynosi 1. Pamiętaj o jedynce!
Czyli, jeśli chcemy pomnożyć ułamek a/b przez liczbę całkowitą c, to:
a/b * c = a/b * c/1 = a*c/b
Na przykład:
3/4 * 5 = 3/4 * 5/1 = 3*5/4 = 15/4
Ułamek 15/4 możemy przedstawić jako liczbę mieszaną: 33/4.
Dzielenie Ułamków Zwykłych
Zasady Dzielenia
Dzielenie ułamków zwykłych jest nieco bardziej skomplikowane niż mnożenie, ale w gruncie rzeczy sprowadza się do mnożenia przez odwrotność dzielnika. Zapamiętaj: Odwrotność!
Odwrotnością ułamka a/b jest ułamek b/a. Aby podzielić ułamek przez inny ułamek, mnożymy dzielną przez odwrotność dzielnika.
Formalnie, jeśli mamy dwa ułamki a/b oraz c/d, ich iloraz wynosi:
a/b : c/d = a/b * d/c = a*d/b*c
Na przykład:
1/2 : 2/3 = 1/2 * 3/2 = 1*3/2*2 = 3/4
Dzielenie Ułamków przez Liczby Całkowite
Dzielenie ułamka przez liczbę całkowitą jest równoważne mnożeniu ułamka przez odwrotność tej liczby całkowitej. Odwrotnością liczby całkowitej *c* jest 1/c. Pomyśl o tym!
Czyli, jeśli chcemy podzielić ułamek a/b przez liczbę całkowitą c, to:
a/b : c = a/b : c/1 = a/b * 1/c = a/b*c
Na przykład:
3/4 : 5 = 3/4 : 5/1 = 3/4 * 1/5 = 3/20
Dzielenie Liczby Całkowitej przez Ułamek
Dzielenie liczby całkowitej przez ułamek polega na pomnożeniu liczby całkowitej przez odwrotność ułamka. To prosta zamiana!
Czyli, jeśli chcemy podzielić liczbę całkowitą c przez ułamek a/b, to:
c : a/b = c/1 : a/b = c/1 * b/a = c*b/a
Na przykład:
5 : 3/4 = 5/1 : 3/4 = 5/1 * 4/3 = 20/3
Ułamek 20/3 możemy przedstawić jako liczbę mieszaną: 62/3.
Przykłady z Życia Codziennego
Umiejętność mnożenia i dzielenia ułamków znajduje zastosowanie w wielu sytuacjach życiowych. Oto kilka przykładów:
* Gotowanie: Przepisy często podają ilości składników w ułamkach. Jeśli chcemy podwoić lub zmniejszyć przepis o połowę, musimy mnożyć lub dzielić ułamki. Na przykład, jeśli przepis wymaga 2/3 szklanki mąki, a chcemy zrobić połowę przepisu, musimy pomnożyć 2/3 przez 1/2, co daje 1/3 szklanki mąki. * Budownictwo: Podczas mierzenia i cięcia materiałów, takich jak drewno lub tkanina, często spotykamy się z ułamkami. Jeśli musimy pociąć deskę o długości 31/2 metra na 5 równych części, musimy podzielić 31/2 przez 5. * Finanse: Obliczanie rabatów i procentów często wymaga operacji na ułamkach. Jeśli dany produkt jest przeceniony o 1/4 ceny, musimy obliczyć, ile wynosi 1/4 ceny i odjąć to od ceny pierwotnej. * Planowanie podróży: Jeśli wiemy, że pokonaliśmy 3/5 trasy o długości 200 km, możemy obliczyć, ile kilometrów nam zostało do przejechania.Podsumowanie
Mnożenie i dzielenie ułamków zwykłych są fundamentalnymi operacjami matematycznymi o szerokim zastosowaniu w życiu codziennym. Kluczem do sukcesu jest zrozumienie zasad i regularna praktyka. Ćwicz, ćwicz, ćwicz! Pamiętajmy, że mnożenie polega na mnożeniu liczników i mianowników, a dzielenie na mnożeniu przez odwrotność dzielnika. Upraszczanie ułamków przed wykonaniem operacji może znacznie ułatwić obliczenia.
Zachęcamy do ćwiczenia mnożenia i dzielenia ułamków w różnych kontekstach, aby utrwalić wiedzę i nabrać pewności w ich stosowaniu. Spróbuj rozwiązać kilka przykładów ze swojego otoczenia – oblicz, ile składników potrzebujesz do połowy przepisu na ulubione ciasto, lub oblicz, ile metrów kwadratowych płytek potrzebujesz do wyłożenia łazienki. Im więcej będziesz ćwiczyć, tym łatwiej będzie Ci radzić sobie z ułamkami w przyszłości. Powodzenia!