Ułamki Zwykłe I Liczby Mieszane Klasa 5 Karty Pracy

Witajcie, drodzy uczniowie klasy 5! Dziś porozmawiamy o ułamkach zwykłych i liczbach mieszanych. Wiem, że na początku mogą wydawać się trochę trudne, ale obiecuję, że po dzisiejszej lekcji wszystko stanie się jasne i zrozumiałe. Przygotowałem też dla Was kilka wskazówek dotyczących kart pracy, które pomogą Wam utrwalić zdobytą wiedzę.

Zacznijmy od podstaw.

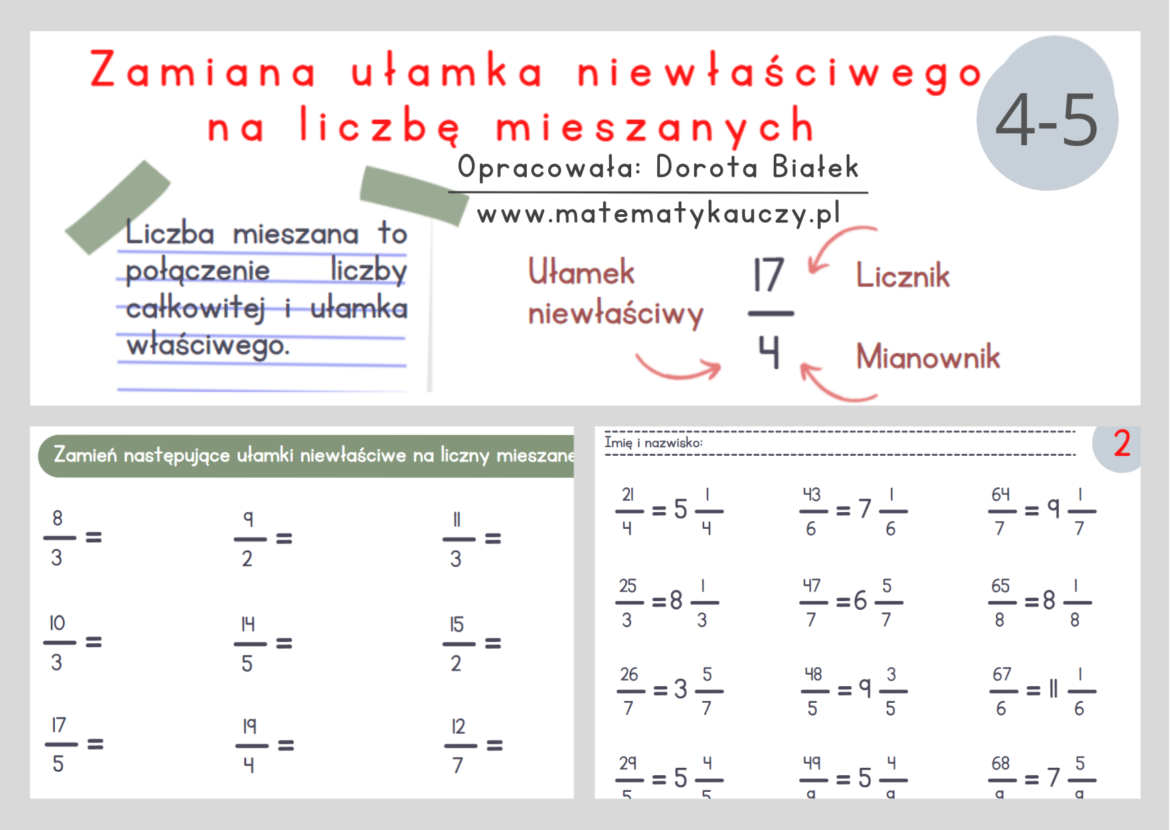
Ułamek zwykły to po prostu sposób na przedstawienie części całości. Wyobraźcie sobie pizzę podzieloną na 8 kawałków. Jeśli zjecie 3 kawałki, to zjedliście 3/8 pizzy. Górna liczba w ułamku (w tym przypadku 3) to licznik. Licznik mówi nam, ile części mamy. Dolna liczba (w tym przypadku 8) to mianownik. Mianownik mówi nam, na ile części całość została podzielona.

Ułamek zapisujemy w formie: licznik/mianownik. Pamiętajcie, że mianownik nigdy nie może być zerem! Nie da się podzielić czegoś na zero części.

Rodzaje ułamków

Mamy kilka rodzajów ułamków. Najważniejsze to:

Ułamki właściwe: To ułamki, w których licznik jest mniejszy od mianownika. Na przykład: 1/2, 3/4, 5/7. Te ułamki są mniejsze od 1.
Ułamki niewłaściwe: To ułamki, w których licznik jest większy lub równy mianownikowi. Na przykład: 5/3, 7/7, 9/2. Te ułamki są większe lub równe 1.
Liczby mieszane: To połączenie liczby całkowitej i ułamka właściwego. Na przykład: 1 1/2, 2 3/4, 5 1/3. Liczby mieszane reprezentują wartość większą od 1.

Zamiana ułamków niewłaściwych na liczby mieszane i odwrotnie

To bardzo ważna umiejętność!

Zamiana ułamka niewłaściwego na liczbę mieszaną:

Podziel licznik przez mianownik. Wynik dzielenia to liczba całkowita w liczbie mieszanej. Reszta z dzielenia to licznik ułamka w liczbie mieszanej. Mianownik pozostaje ten sam.

Na przykład: Zamieńmy ułamek 7/3 na liczbę mieszaną.

7 podzielone przez 3 to 2, reszta 1. Więc 7/3 to 2 1/3.

Zamiana liczby mieszanej na ułamek niewłaściwy:

Pomnóż liczbę całkowitą przez mianownik ułamka. Dodaj wynik do licznika ułamka. Wynik to licznik ułamka niewłaściwego. Mianownik pozostaje ten sam.

Na przykład: Zamieńmy liczbę mieszaną 3 1/4 na ułamek niewłaściwy.

3 pomnożone przez 4 to 12. Dodaj 1, otrzymasz 13. Więc 3 1/4 to 13/4.

Rozszerzanie i skracanie ułamków

Rozszerzanie ułamków: Polega na pomnożeniu licznika i mianownika przez tę samą liczbę. Wartość ułamka się nie zmienia, tylko zapis jest inny.

Na przykład: Rozszerzmy ułamek 1/2 przez 3.

1 pomnożone przez 3 to 3. 2 pomnożone przez 3 to 6. Więc 1/2 = 3/6.

Skracanie ułamków: Polega na podzieleniu licznika i mianownika przez tę samą liczbę. Wartość ułamka się nie zmienia, tylko zapis jest inny. Dążymy do tego, aby ułamek był w najprostszej postaci (nie dało się go już skrócić).

Na przykład: Skróćmy ułamek 4/8 przez 4.

4 podzielone przez 4 to 1. 8 podzielone przez 4 to 2. Więc 4/8 = 1/2.

Dodawanie i odejmowanie ułamków

Aby dodać lub odjąć ułamki, muszą mieć one ten sam mianownik. Jeśli tak nie jest, musimy je sprowadzić do wspólnego mianownika (czyli znaleźć taki sam mianownik dla obu ułamków). Najczęściej szukamy najmniejszej wspólnej wielokrotności (NWW) mianowników.

Dodawanie ułamków o tych samych mianownikach: Dodajemy liczniki, a mianownik pozostaje ten sam.

Na przykład: 2/5 + 1/5 = (2+1)/5 = 3/5

Odejmowanie ułamków o tych samych mianownikach: Odejmujemy liczniki, a mianownik pozostaje ten sam.

Na przykład: 4/7 - 1/7 = (4-1)/7 = 3/7

Dodawanie i odejmowanie ułamków o różnych mianownikach: Najpierw sprowadzamy ułamki do wspólnego mianownika, a następnie dodajemy lub odejmujemy liczniki.

Na przykład: 1/2 + 1/3. Wspólny mianownik dla 2 i 3 to 6. Rozszerzamy 1/2 przez 3, otrzymujemy 3/6. Rozszerzamy 1/3 przez 2, otrzymujemy 2/6. Teraz możemy dodać: 3/6 + 2/6 = 5/6.

Dodawanie i odejmowanie liczb mieszanych

Możemy dodawać i odejmować liczby mieszane na dwa sposoby:

Sposób 1: Zamieniamy liczby mieszane na ułamki niewłaściwe, a następnie dodajemy lub odejmujemy ułamki.
Sposób 2: Dodajemy lub odejmujemy oddzielnie liczby całkowite i ułamki. Jeśli po dodaniu ułamków otrzymamy ułamek niewłaściwy, zamieniamy go na liczbę mieszaną i dodajemy liczbę całkowitą do wcześniej uzyskanej liczby całkowitej. Przy odejmowaniu, jeśli ułamek od którego odejmujemy jest mniejszy od ułamka, który odejmujemy, musimy "pożyczyć" 1 z liczby całkowitej i zamienić ją na ułamek o odpowiednim mianowniku.

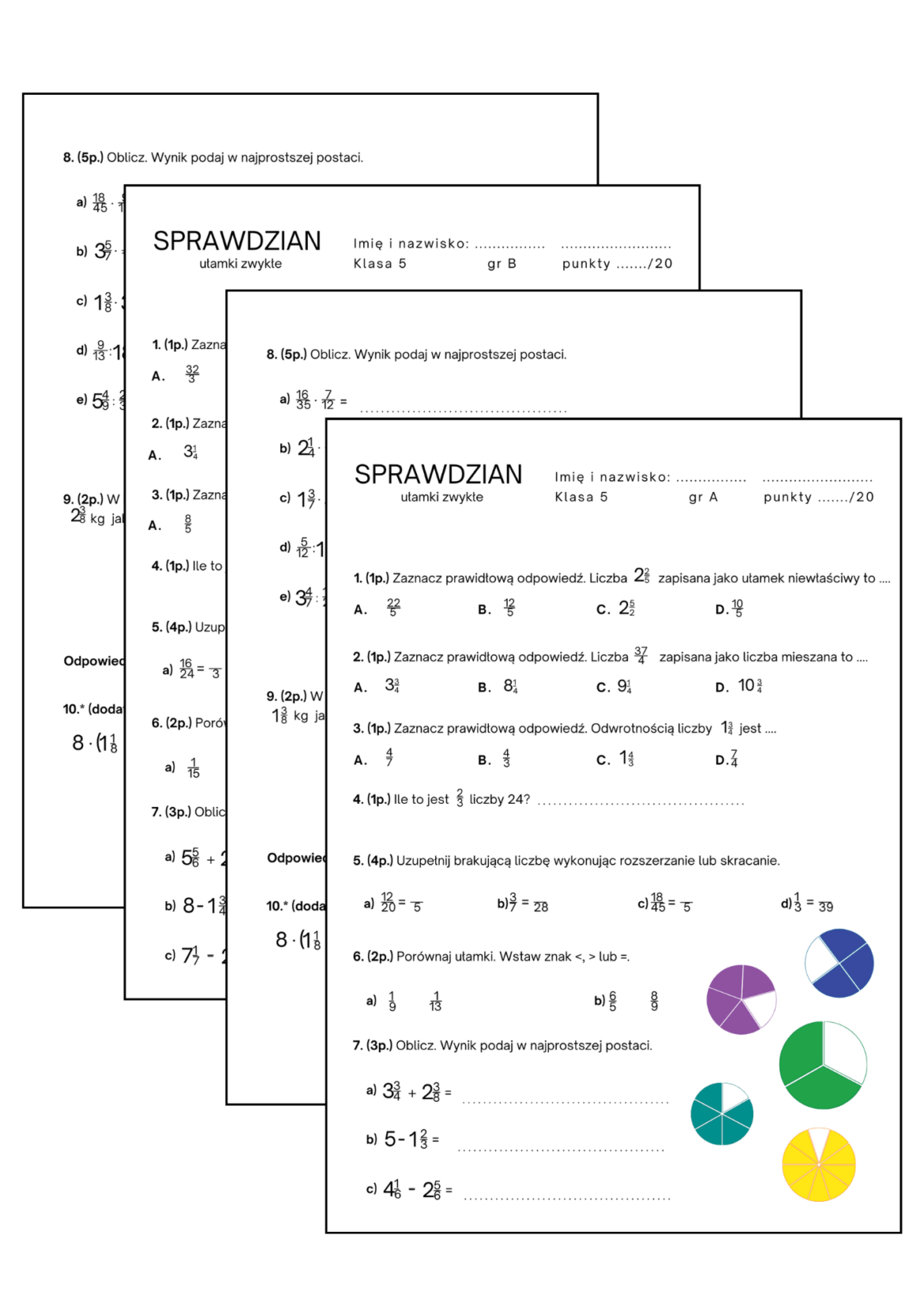
Karty pracy – jak efektywnie z nich korzystać

Teraz kilka słów o kartach pracy. Karty pracy to świetny sposób na utrwalenie wiedzy i sprawdzenie, czy wszystko dobrze rozumiecie.

Czytaj uważnie polecenia: To podstawa! Zanim zaczniesz rozwiązywać zadanie, upewnij się, że dokładnie wiesz, co masz zrobić.
Rób zadania po kolei: Nie przeskakuj z zadania na zadanie. Staraj się rozwiązywać je po kolei, zaczynając od najłatwiejszych.
Zapisuj swoje obliczenia: Nawet jeśli potrafisz rozwiązać zadanie w pamięci, zapisuj swoje obliczenia. Dzięki temu łatwiej będzie Ci sprawdzić, gdzie ewentualnie popełniłeś błąd.
Sprawdzaj swoje odpowiedzi: Po rozwiązaniu wszystkich zadań, sprawdź swoje odpowiedzi. Możesz poprosić o pomoc rodzica, starszego rodzeństwa lub nauczyciela.
Nie zrażaj się trudnościami: Jeśli nie wiesz, jak rozwiązać zadanie, nie poddawaj się! Spróbuj jeszcze raz, przeczytaj jeszcze raz teorię, poszukaj podobnych przykładów w podręczniku lub w Internecie. Możesz też poprosić o pomoc kolegę z klasy lub nauczyciela.
Wykorzystuj różne rodzaje zadań: Karty pracy często zawierają różne rodzaje zadań, takie jak: rozwiązywanie przykładów, uzupełnianie luk, rysowanie, rozwiązywanie zadań tekstowych. Staraj się wykorzystywać wszystkie rodzaje zadań, aby ćwiczyć różne umiejętności.

H2: Przykładowe zadania z kart pracy i jak je rozwiązywać

Oto kilka przykładowych zadań, które mogą pojawić się na kartach pracy, wraz z objaśnieniami, jak je rozwiązywać:

Zamień ułamek niewłaściwy na liczbę mieszaną: 11/4

Rozwiązanie: Dzielimy 11 przez 4. Otrzymujemy 2, reszta 3. Więc 11/4 = 2 3/4.
Zamień liczbę mieszaną na ułamek niewłaściwy: 2 1/5

Rozwiązanie: Mnożymy 2 przez 5, otrzymujemy 10. Dodajemy 1, otrzymujemy 11. Więc 2 1/5 = 11/5.
Rozszerz ułamek 2/3 przez 4:

Rozwiązanie: Mnożymy 2 przez 4, otrzymujemy 8. Mnożymy 3 przez 4, otrzymujemy 12. Więc 2/3 = 8/12.
Skróć ułamek 6/9 przez 3:

Rozwiązanie: Dzielimy 6 przez 3, otrzymujemy 2. Dzielimy 9 przez 3, otrzymujemy 3. Więc 6/9 = 2/3.
Dodaj ułamki: 1/4 + 2/4

Rozwiązanie: Dodajemy liczniki: 1 + 2 = 3. Mianownik pozostaje ten sam. Więc 1/4 + 2/4 = 3/4.
Odejmij ułamki: 5/8 - 2/8

Rozwiązanie: Odejmujemy liczniki: 5 - 2 = 3. Mianownik pozostaje ten sam. Więc 5/8 - 2/8 = 3/8.
Dodaj ułamki o różnych mianownikach: 1/2 + 1/4

Rozwiązanie: Wspólny mianownik dla 2 i 4 to 4. Rozszerzamy 1/2 przez 2, otrzymujemy 2/4. Teraz możemy dodać: 2/4 + 1/4 = 3/4.
Odejmij ułamki o różnych mianownikach: 2/3 - 1/6

Rozwiązanie: Wspólny mianownik dla 3 i 6 to 6. Rozszerzamy 2/3 przez 2, otrzymujemy 4/6. Teraz możemy odjąć: 4/6 - 1/6 = 3/6. Możemy jeszcze skrócić ułamek 3/6 przez 3, otrzymujemy 1/2.
Dodaj liczby mieszane: 1 1/2 + 2 1/4

Rozwiązanie (Sposób 1): Zamieniamy liczby mieszane na ułamki niewłaściwe: 1 1/2 = 3/2, 2 1/4 = 9/4. Wspólny mianownik dla 2 i 4 to 4. Rozszerzamy 3/2 przez 2, otrzymujemy 6/4. Teraz możemy dodać: 6/4 + 9/4 = 15/4. Zamieniamy 15/4 na liczbę mieszaną: 15/4 = 3 3/4. Rozwiązanie (Sposób 2): Dodajemy liczby całkowite: 1 + 2 = 3. Dodajemy ułamki: 1/2 + 1/4 = 3/4 (jak w przykładzie 7). Więc 1 1/2 + 2 1/4 = 3 3/4.
Odejmij liczby mieszane: 3 1/3 - 1 1/6

Rozwiązanie (Sposób 1): Zamieniamy liczby mieszane na ułamki niewłaściwe: 3 1/3 = 10/3, 1 1/6 = 7/6. Wspólny mianownik dla 3 i 6 to 6. Rozszerzamy 10/3 przez 2, otrzymujemy 20/6. Teraz możemy odjąć: 20/6 - 7/6 = 13/6. Zamieniamy 13/6 na liczbę mieszaną: 13/6 = 2 1/6. Rozwiązanie (Sposób 2): Odejmujemy liczby całkowite: 3 - 1 = 2. Odejmujemy ułamki: 1/3 - 1/6 = 1/6 (jak w przykładzie 8). Więc 3 1/3 - 1 1/6 = 2 1/6.

H2: Dodatkowe wskazówki

Pamiętaj o upraszczaniu wyników: Jeśli to możliwe, skracaj ułamki do najprostszej postaci.
Używaj rysunków: Jeśli masz problem z rozwiązaniem zadania, spróbuj narysować sobie sytuację. Na przykład, jeśli masz dodać 1/2 i 1/4, możesz narysować koło podzielone na 2 części i pokolorować 1 część, a następnie narysować drugie koło podzielone na 4 części i pokolorować 1 część. Wtedy łatwiej będzie Ci zobaczyć, ile to razem.
Graj w gry: Istnieje wiele gier online, które pomagają w nauce ułamków. Możesz spróbować poszukać takich gier i uczyć się przez zabawę.

H2: Gdzie szukać pomocy?

Jeśli nadal masz problemy z ułamkami, nie martw się! Istnieje wiele miejsc, gdzie możesz szukać pomocy:

Zapytaj nauczyciela: Twój nauczyciel jest najlepszym źródłem informacji. Możesz poprosić go o pomoc podczas lekcji lub po lekcjach.
Poproś o pomoc rodzica lub starszego rodzeństwa: Oni też mogą Ci pomóc zrozumieć ułamki.
Korzystaj z podręcznika i zeszytu: W podręczniku i zeszycie znajdziesz wszystkie potrzebne informacje i przykłady.
Szukaj informacji w Internecie: W Internecie znajdziesz wiele stron internetowych i filmów edukacyjnych, które pomogą Ci zrozumieć ułamki.

Pamiętaj, że nauka ułamków wymaga czasu i ćwiczeń. Nie zrażaj się trudnościami i regularnie ćwicz, a na pewno opanujesz tę umiejętność! Powodzenia!