Ulamki Zwykle I Dziesietne Sprawdzian 1 Klasa 6

Witaj! Porozmawiamy dzisiaj o ułamkach zwykłych i dziesiętnych. To bardzo ważne pojęcia w matematyce. Często spotykamy się z nimi w życiu codziennym. Pamiętaj, że zrozumienie ułamków jest kluczowe do dalszej nauki matematyki.
Ułamki Zwykłe
Ułamek zwykły to liczba, która przedstawia część całości. Składa się z licznika i mianownika. Licznik znajduje się na górze kreski ułamkowej. Mianownik znajduje się na dole kreski ułamkowej.
Na przykład, w ułamku 1/2, 1 to licznik, a 2 to mianownik. Oznacza to, że całość została podzielona na dwie równe części, a my bierzemy jedną z nich. Inny przykład to 3/4. Tutaj mamy trzy części z czterech.
Ułamki zwykłe możemy skracać i rozszerzać. Skracanie polega na podzieleniu licznika i mianownika przez ten sam numer. Rozszerzanie to pomnożenie licznika i mianownika przez ten sam numer. 2/4 można skrócić do 1/2. 1/2 można rozszerzyć do 2/4 lub 3/6.
Ułamki Dziesiętne
Ułamek dziesiętny to inna forma zapisu ułamka. Wykorzystuje przecinek do oddzielenia części całkowitej od części ułamkowej. Ułamki dziesiętne łatwo zamienić na zwykłe i odwrotnie.
Na przykład, 0,5 to ułamek dziesiętny. Czytamy go "zero i pięć dziesiątych". Możemy go zapisać jako ułamek zwykły: 5/10, co po skróceniu daje 1/2. Inny przykład to 1,75, czyli "jeden i siedemdziesiąt pięć setnych". To jest to samo co 175/100, czyli 13/4 po skróceniu.
Dodawanie i odejmowanie ułamków dziesiętnych jest proste. Ważne jest, aby wyrównać przecinki. Na przykład: 2,3 + 1,4 = 3,7. Podobnie: 5,8 - 2,1 = 3,7.
Zamiana Ułamków
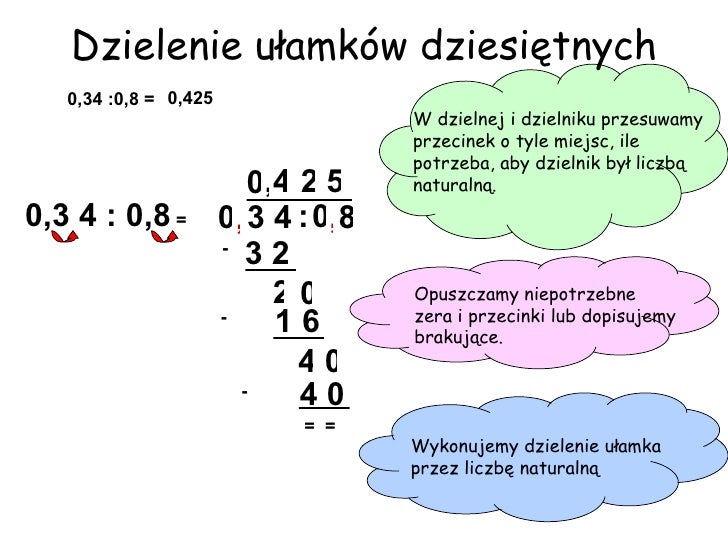
Ułamek zwykły można zamienić na dziesiętny dzieląc licznik przez mianownik. Na przykład, 1/4 to 1 podzielone przez 4, co daje 0,25. Niektóre ułamki zwykłe mają rozwinięcia dziesiętne skończone (np. 1/4 = 0,25), a inne – nieskończone (np. 1/3 = 0,333...).
Ułamek dziesiętny można zamienić na zwykły zapisując go jako ułamek z mianownikiem będącym potęgą liczby 10 (10, 100, 1000, itd.). Następnie można go skrócić. Na przykład, 0,75 to 75/100, co po skróceniu daje 3/4.
Pamiętaj o ćwiczeniach! Im więcej rozwiązujesz zadań, tym lepiej rozumiesz ułamki. Powodzenia na sprawdzianie w klasie 6!