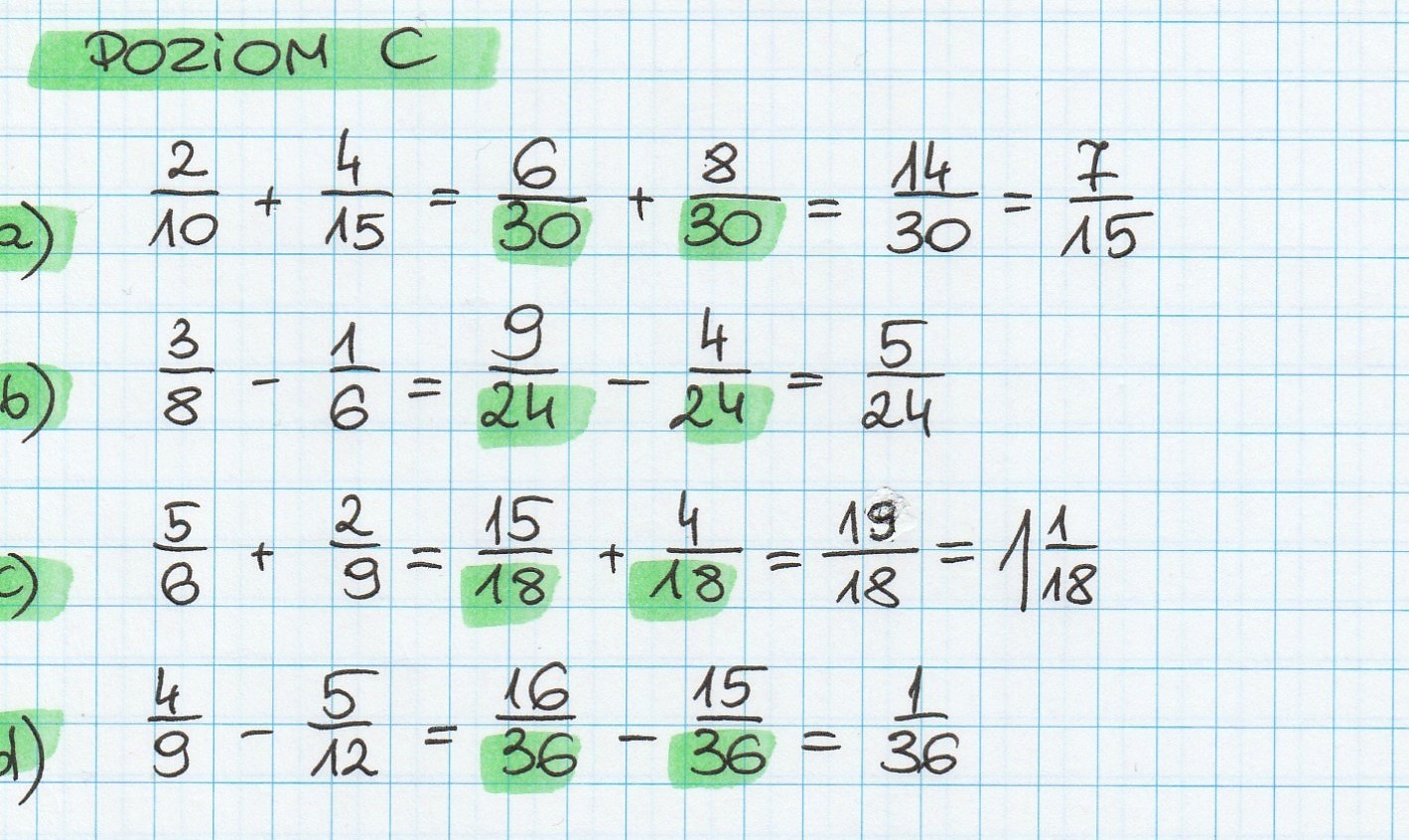Ulamki Zwykle Dodawanie I Odejmowanie Sprawdzian Klasa 5

Czy ułamki zwykłe spędzają Ci sen z powiek? Nie martw się! Ten artykuł pomoże Ci zrozumieć dodawanie i odejmowanie ułamków zwykłych, tak aby sprawdzian z tego tematu w 5 klasie nie był już powodem do stresu. Razem przejdziemy przez wszystkie najważniejsze zagadnienia, wyjaśnimy trudne kwestie i pokażemy, jak rozwiązywać zadania krok po kroku. Przygotuj się na solidną dawkę wiedzy podaną w przystępny sposób!
Co to są ułamki zwykłe? Przypomnienie podstaw
Zanim przejdziemy do dodawania i odejmowania, przypomnijmy sobie, czym w ogóle są ułamki zwykłe. Ułamek zwykły to sposób zapisu części całości. Składa się z dwóch elementów:
- Licznika – czyli liczby znajdującej się nad kreską ułamkową. Mówi nam, ile części całości bierzemy.
- Mianownika – czyli liczby znajdującej się pod kreską ułamkową. Mówi nam, na ile równych części została podzielona całość.
Na przykład, ułamek 3/4 oznacza, że całość została podzielona na 4 równe części, a my bierzemy 3 z nich. Pamiętaj, że mianownik nigdy nie może być zerem!
Dodawanie ułamków zwykłych – krok po kroku
Dodawanie ułamków zwykłych może wydawać się trudne, ale w rzeczywistości jest całkiem proste, o ile pamiętasz o kilku zasadach. Najważniejsza zasada to:
Dodawanie ułamków o jednakowych mianownikach
Jeśli ułamki, które chcesz dodać, mają jednakowe mianowniki, to wystarczy dodać do siebie liczniki, a mianownik pozostawić bez zmian.
Przykład:
2/5 + 1/5 = (2+1)/5 = 3/5
Czyli, jeśli masz dwa kawałki tortu (dwa piąte tortu) i dodasz do nich jeszcze jeden kawałek (jedną piątą tortu), to razem będziesz mieć trzy kawałki (trzy piąte tortu).
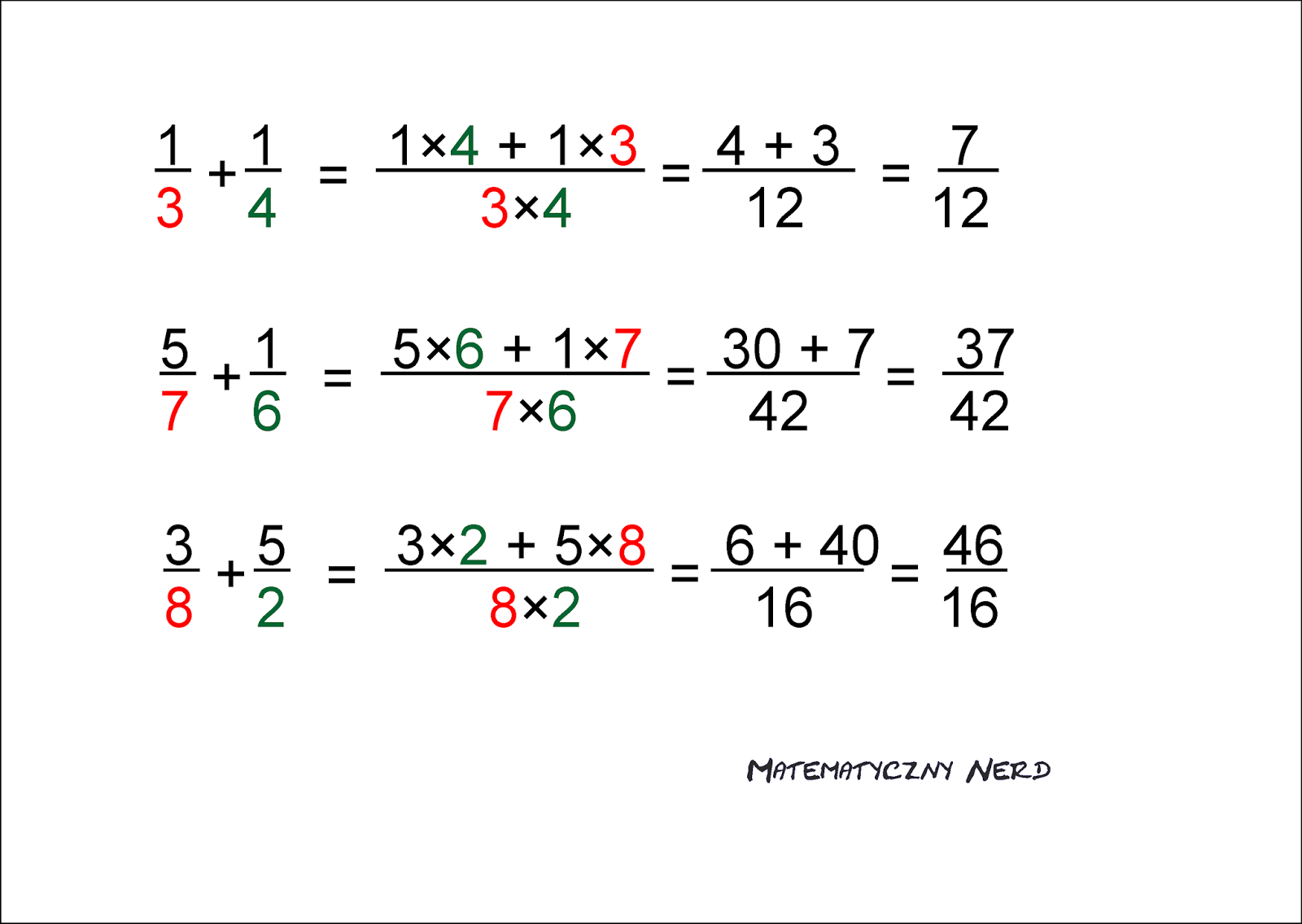
Dodawanie ułamków o różnych mianownikach
A co zrobić, jeśli ułamki mają różne mianowniki? Wtedy musimy najpierw sprowadzić je do wspólnego mianownika. Wspólny mianownik to liczba, która dzieli się przez wszystkie mianowniki, które mamy. Najczęściej szukamy najmniejszej wspólnej wielokrotności (NWW) mianowników.
Przykład:
1/2 + 1/3 = ?
Mianowniki to 2 i 3. NWW(2, 3) = 6. Musimy więc zamienić oba ułamki na takie, które mają mianownik 6.
- 1/2 = (1 * 3)/(2 * 3) = 3/6
- 1/3 = (1 * 2)/(3 * 2) = 2/6
Teraz możemy dodać:
3/6 + 2/6 = (3+2)/6 = 5/6
Wskazówka: Aby znaleźć NWW, możesz wypisać wielokrotności każdej liczby, aż znajdziesz wspólną. Na przykład: wielokrotności 2 to 2, 4, 6, 8, 10... a wielokrotności 3 to 3, 6, 9, 12...
Odejmowanie ułamków zwykłych – analogicznie do dodawania
Odejmowanie ułamków zwykłych działa bardzo podobnie do dodawania. Pamiętaj tylko, żeby zamiast dodawać liczniki, odejmować je od siebie!
Odejmowanie ułamków o jednakowych mianownikach
Jeśli ułamki mają jednakowe mianowniki, odejmujemy liczniki, a mianownik zostawiamy bez zmian.
Przykład:
4/7 - 1/7 = (4-1)/7 = 3/7
Odejmowanie ułamków o różnych mianownikach
Jeśli ułamki mają różne mianowniki, tak jak przy dodawaniu, musimy najpierw sprowadzić je do wspólnego mianownika.
Przykład:
2/3 - 1/4 = ?
Mianowniki to 3 i 4. NWW(3, 4) = 12. Musimy więc zamienić oba ułamki na takie, które mają mianownik 12.
- 2/3 = (2 * 4)/(3 * 4) = 8/12
- 1/4 = (1 * 3)/(4 * 3) = 3/12
Teraz możemy odjąć:
8/12 - 3/12 = (8-3)/12 = 5/12
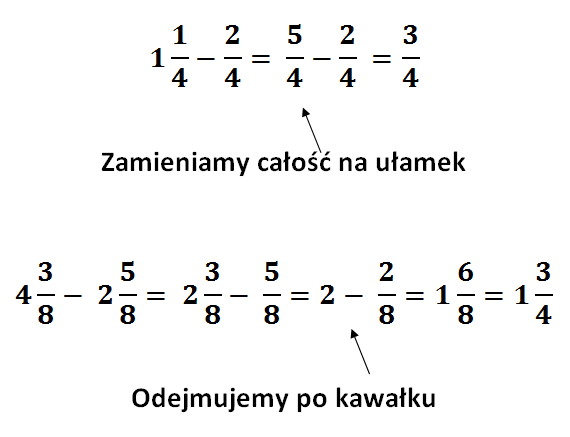
Ułamki niewłaściwe i liczby mieszane
Czasami, dodając ułamki, możemy otrzymać ułamek niewłaściwy. Ułamek niewłaściwy to taki, w którym licznik jest większy lub równy mianownikowi. Na przykład: 7/3.
Ułamek niewłaściwy możemy zamienić na liczbę mieszaną. Liczba mieszana składa się z liczby całkowitej i ułamka zwykłego.
Jak zamienić ułamek niewłaściwy na liczbę mieszaną?
- Podziel licznik przez mianownik.
- Wynik dzielenia (bez reszty) to liczba całkowita.
- Reszta z dzielenia to licznik ułamka.
- Mianownik ułamka pozostaje taki sam.
Przykład:
7/3 = 7 : 3 = 2 reszty 1
Czyli 7/3 = 2 1/3
Jak zamienić liczbę mieszaną na ułamek niewłaściwy?
- Pomnóż liczbę całkowitą przez mianownik ułamka.
- Dodaj wynik do licznika ułamka.
- Otrzymana suma to nowy licznik ułamka.
- Mianownik ułamka pozostaje taki sam.
Przykład:
2 1/3 = (2 * 3 + 1) / 3 = 7 / 3
Upraszczanie ułamków
Pamiętaj, żeby zawsze upraszczać ułamki, jeśli to możliwe. Upraszczanie polega na podzieleniu licznika i mianownika przez ich wspólny dzielnik, aż do uzyskania ułamka, którego nie da się już bardziej uprościć. Mówimy wtedy, że ułamek jest w postaci nieskracalnej.
Przykład:
6/8 = (6 : 2)/(8 : 2) = 3/4
W tym przypadku podzieliliśmy zarówno licznik, jak i mianownik przez 2, ponieważ 2 jest ich wspólnym dzielnikiem.
Przykładowe zadania ze sprawdzianu i ich rozwiązania
Aby jeszcze lepiej przygotować Cię do sprawdzianu, rozwiążmy razem kilka przykładowych zadań:
- Oblicz: 1/4 + 2/4 = ?
- Oblicz: 1/2 + 1/5 = ?
- Oblicz: 3/5 - 1/5 = ?
- Oblicz: 2/3 - 1/6 = ?
- Zamień ułamek niewłaściwy na liczbę mieszaną: 11/4 = ?
- Zamień liczbę mieszaną na ułamek niewłaściwy: 3 1/2 = ?
Rozwiązanie: Ułamki mają jednakowe mianowniki, więc dodajemy liczniki: 1/4 + 2/4 = 3/4
Rozwiązanie: Ułamki mają różne mianowniki, więc musimy sprowadzić je do wspólnego mianownika. NWW(2, 5) = 10. Zatem: 1/2 = 5/10 i 1/5 = 2/10. Teraz możemy dodać: 5/10 + 2/10 = 7/10
Rozwiązanie: Ułamki mają jednakowe mianowniki, więc odejmujemy liczniki: 3/5 - 1/5 = 2/5
Rozwiązanie: Ułamki mają różne mianowniki, więc musimy sprowadzić je do wspólnego mianownika. NWW(3, 6) = 6. Zatem: 2/3 = 4/6. Teraz możemy odjąć: 4/6 - 1/6 = 3/6. Ułamek możemy uprościć: 3/6 = 1/2
Rozwiązanie: 11 : 4 = 2 reszty 3. Zatem: 11/4 = 2 3/4
Rozwiązanie: (3 * 2 + 1) / 2 = 7 / 2. Zatem: 3 1/2 = 7/2
Dodatkowe wskazówki na sprawdzian
- Przeczytaj uważnie treść zadania. Upewnij się, że wiesz, o co pytają.
- Pisz czytelnie. Nauczyciel musi móc odczytać Twoje rozwiązanie.
- Sprawdzaj swoje obliczenia. Unikniesz w ten sposób prostych błędów.
- Upraszczaj ułamki. Zawsze, gdy to możliwe, doprowadź ułamek do postaci nieskracalnej.
- Nie panikuj! Nawet jeśli nie wiesz, jak rozwiązać jakieś zadanie, spróbuj podejść do niego krok po kroku.
Pamiętaj, że praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz dodawanie i odejmowanie ułamków zwykłych i tym pewniej poczujesz się na sprawdzianie. Powodzenia!
Mam nadzieję, że ten artykuł okazał się pomocny. Teraz z pewnością dasz radę na sprawdzianie z ułamków zwykłych w 5 klasie! Pamiętaj o wszystkich omówionych zasadach i wskazówkach, a sukces jest gwarantowany. Powodzenia!