Ułamki Zwykłe Dodawanie I Odejmowanie

Hej! Słyszałeś kiedyś o ułamkach zwykłych? Pewnie tak! Ale czy wiesz, że dodawanie i odejmowanie ich może być naprawdę niezłą zabawą? Tak, dobrze słyszysz! Zapomnij o nudnych lekcjach matematyki. To przygoda, obietnica niespodzianek i trochę magii!

Wkrocz do świata Ułamków!

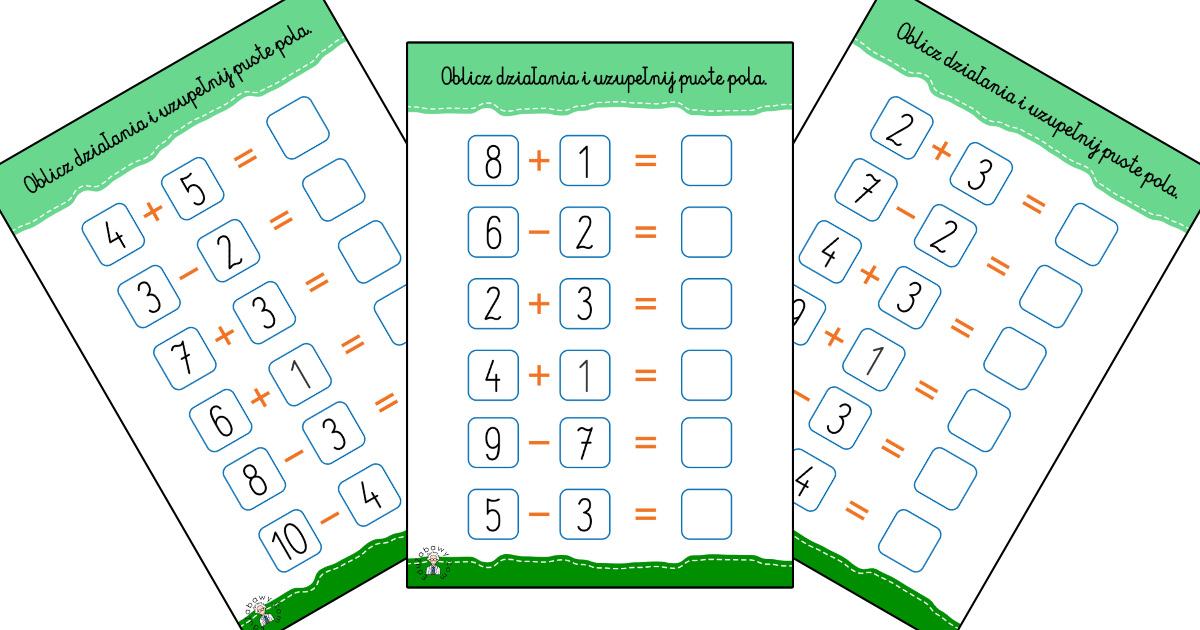
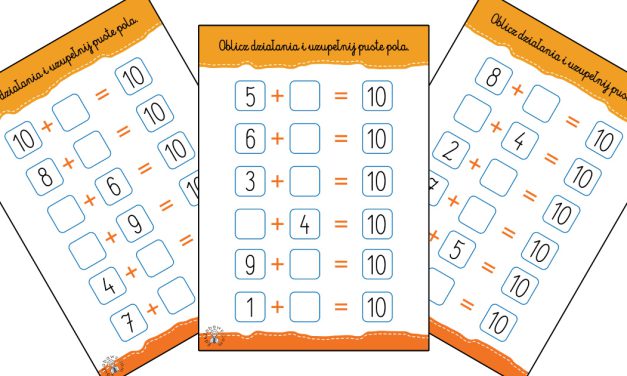
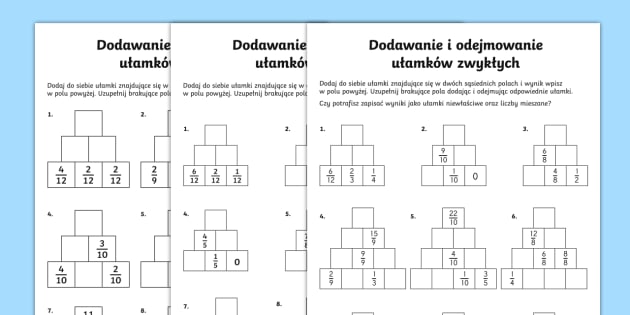
Wyobraź sobie, że masz pizzę. Dużą, pyszną pizzę podzieloną na kawałki. Ułamki zwykłe pozwalają nam mówić o tych kawałkach w dokładny sposób. Jeden kawałek z ośmiu to 1/8. Dwa kawałki to 2/8. Widzisz już, o co chodzi? Mówimy o częściach całości!

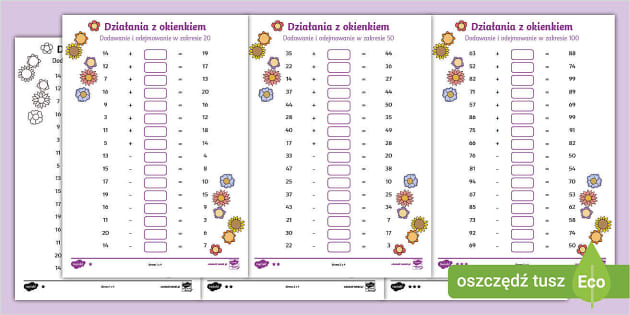
A teraz, dodajmy do tego dodawanie i odejmowanie. Co się stanie, jeśli zjesz 3/8 pizzy, a twój przyjaciel 2/8? Ile pizzy zniknęło? To właśnie jest dodawanie ułamków! A jeśli na początku było 7/8 pizzy, a zniknęło 3/8, ile zostało? Odejmowanie w akcji!

Dlaczego To Jest Takie Fajne?

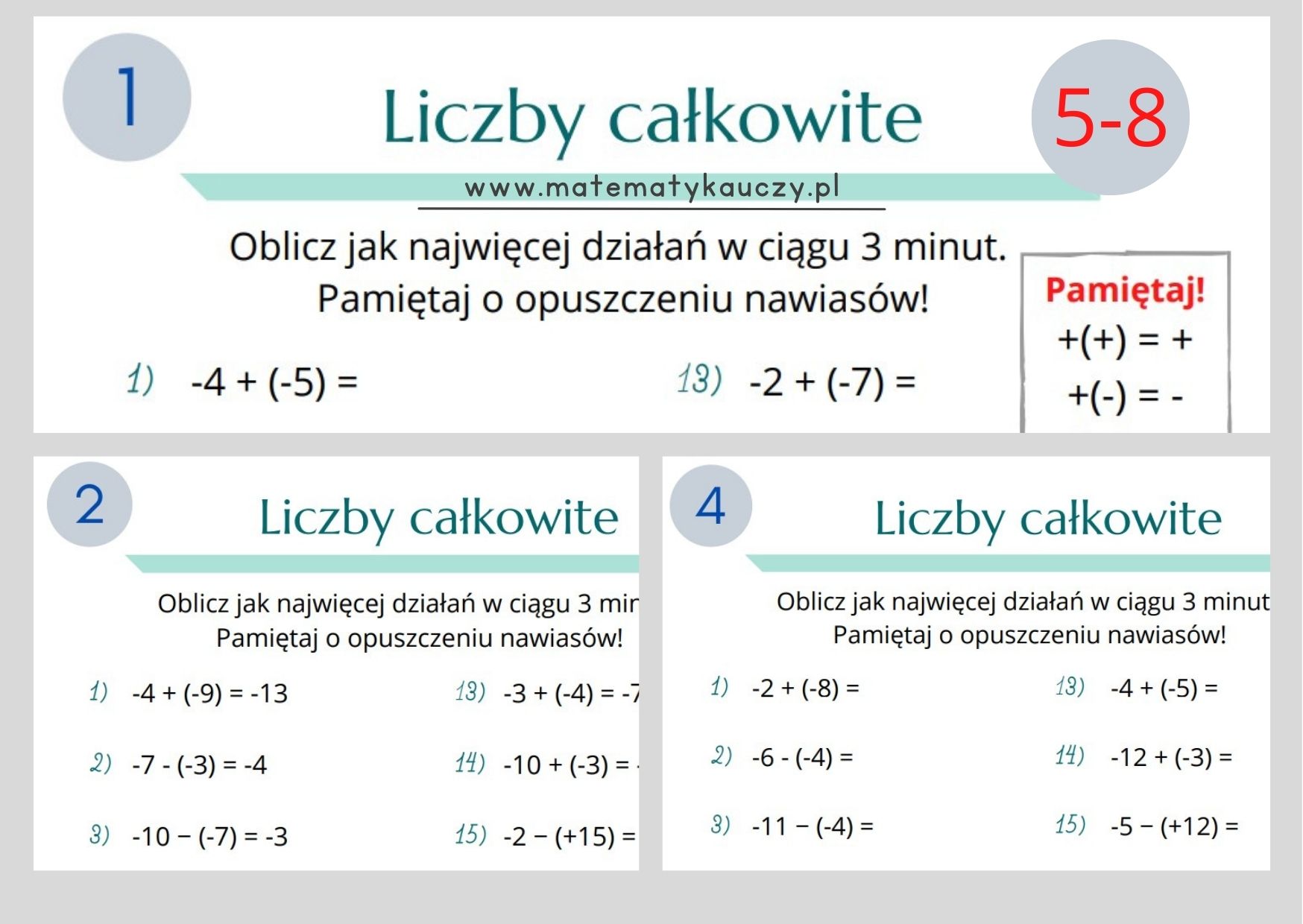
Pomyśl o tym jak o rozwiązywaniu zagadek. Każdy ułamek to mała tajemnica, a dodawanie i odejmowanie to narzędzia detektywa. Musisz połączyć kawałki, znaleźć wspólny mianownik (brzmi strasznie, ale to nic trudnego!), żeby odkryć rozwiązanie.

Oto sekret: wspólny mianownik to klucz do sukcesu! Wyobraź sobie, że dodajesz jabłka do gruszek. Nie bardzo to działa, prawda? Musisz je zamienić na coś wspólnego – owoce! Podobnie jest z ułamkami. Musisz doprowadzić je do tego, żeby miały "ten sam rodzaj" kawałków, zanim zaczniesz dodawać albo odejmować.

"Matematyka to przygoda ducha." – Alfred North Whitehead. A dodawanie i odejmowanie ułamków zwykłych to jej bardzo ciekawy rozdział!

Kiedy już opanujesz tę sztuczkę, zobaczysz, jak bardzo przydatne to jest w życiu. Pieczesz ciasto? Ułamki! Dzielisz się czekoladą z przyjaciółmi? Ułamki! Planujesz remont pokoju? Zgadza się, ułamki!

Nie Bój Się Wyzwania!

Początki bywają trudne, to prawda. Ale nie poddawaj się! Potraktuj to jak grę. Szukaj sposobów na wizualizację ułamków. Rysuj pizzę, ciasto, tabliczki czekolady. Używaj klocków LEGO. Im bardziej kreatywnie podejdziesz do tematu, tym łatwiej go zrozumiesz.

Zamiast traktować to jak żmudne zadanie, spróbuj znaleźć w tym zabawę. Zorganizuj z przyjaciółmi zawody w dodawaniu ułamków. Stwórz własne zadania i łamigłówki. Nagradzaj się za każdy sukces – kawałkiem pizzy, oczywiście!

A pamiętaj, Internet jest pełen wspaniałych zasobów, które mogą Ci pomóc. Znajdziesz tam interaktywne ćwiczenia, filmy instruktażowe i gry, które sprawią, że nauka ułamków stanie się prawdziwą przyjemnością.

Zatem do dzieła! Daj szansę ułamkom zwykłym. Odkryj w sobie detektywa matematycznego. Zaskocz samego siebie, jak wiele możesz się nauczyć i jak wiele radości możesz z tego czerpać. Kto wie, może zostaniesz nowym królem lub królową ułamków!

Powodzenia!