Ułamki Na Osi Liczbowej Klasa 4

Witajcie, młodzi matematycy! W tym artykule przyjrzymy się bliżej jednemu z fascynujących zagadnień matematyki – ułamkom na osi liczbowej. To ważny temat w klasie 4, który pozwala nam wizualizować ułamki i lepiej zrozumieć ich wartość. Gotowi na matematyczną przygodę?

Co to jest Oś Liczbowa?

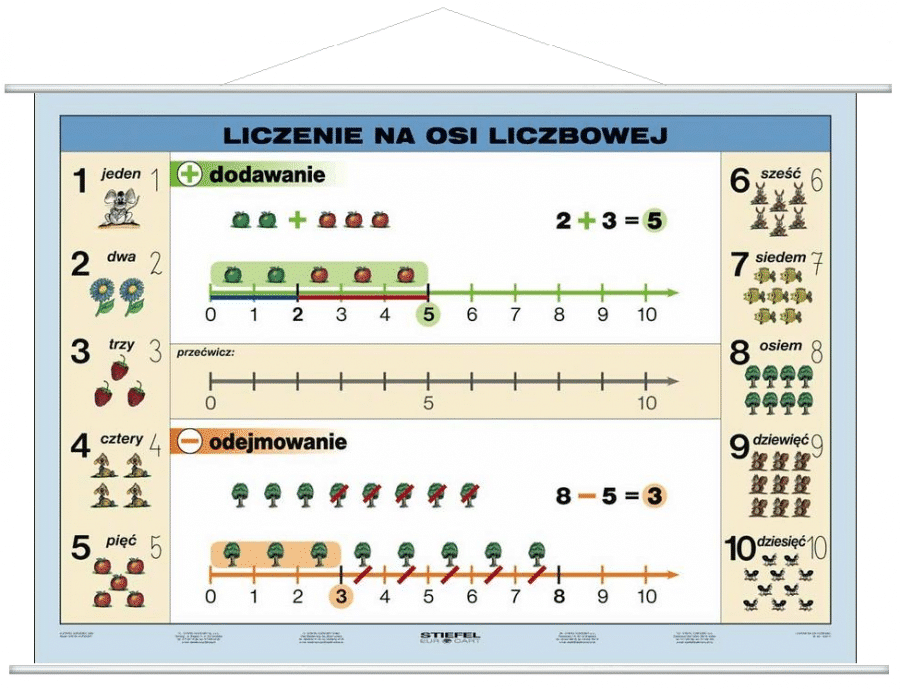
Oś liczbowa to prosta, na której zaznaczamy liczby w kolejności od najmniejszej do największej. Najczęściej oś liczbowa jest pozioma, a zero znajduje się w jej centralnej części. Na prawo od zera znajdują się liczby dodatnie, a na lewo – ujemne. Ale na razie skupimy się na liczbach dodatnich i ułamkach, które są od nich mniejsze.

Wyobraź sobie linijkę, którą masz w piórniku. To jest przykład osi liczbowej! Każdy centymetr to jedna liczba, a pomiędzy centymetrami są mniejsze podziałki. Te mniejsze podziałki mogą reprezentować ułamki!

Ułamki – Przypomnienie Podstaw

Zanim zaczniemy zaznaczać ułamki na osi liczbowej, przypomnijmy sobie, czym właściwie jest ułamek. Ułamek to część całości. Składa się z dwóch liczb: licznika (liczby na górze) i mianownika (liczby na dole), oddzielonych kreską ułamkową.

Mianownik mówi nam, na ile równych części podzielono całość. Licznik mówi nam, ile takich części bierzemy. Na przykład, ułamek 1/2 (jedna druga) oznacza, że całość została podzielona na dwie równe części, a my bierzemy jedną z nich. Ułamek 3/4 (trzy czwarte) oznacza, że całość została podzielona na cztery równe części, a my bierzemy trzy z nich.

Zaznaczanie Ułamków na Osi Liczbowej

Teraz przejdźmy do konkretów! Jak zaznaczyć ułamek na osi liczbowej?

Krok 1: Określ Odcinek Jednostkowy

Odcinek jednostkowy to odcinek na osi liczbowej między liczbami 0 i 1. To nasza "całość", którą będziemy dzielić.

Krok 2: Podziel Odcinek Jednostkowy na Tyle Części, Ile Wynosi Mianownik

Spójrz na mianownik ułamka. To on mówi nam, na ile równych części musimy podzielić odcinek jednostkowy. Na przykład, jeśli chcemy zaznaczyć ułamek 1/3, musimy podzielić odcinek między 0 a 1 na trzy równe części.

Krok 3: Odlicz Tyle Części, Ile Wynosi Licznik

Teraz spójrz na licznik ułamka. Odlicz tyle części od zera, ile wynosi licznik. Miejsce, w którym się zatrzymasz, to pozycja ułamka na osi liczbowej. Dla ułamka 1/3, odliczymy jedną część od zera.

Przykład: Zaznaczmy ułamek 2/5 na osi liczbowej.

1. Określamy odcinek jednostkowy (od 0 do 1).
2. Dzielimy odcinek jednostkowy na 5 równych części (bo mianownik to 5).
3. Odliczamy 2 części od zera (bo licznik to 2).
4. Zaznaczamy punkt na osi liczbowej w tym miejscu. To jest pozycja ułamka 2/5.

Zaznaczanie Ułamków Większych od 1

Co zrobić, jeśli mamy ułamek większy od 1, na przykład 5/4? W takim przypadku potrzebujemy więcej niż jednego odcinka jednostkowego!

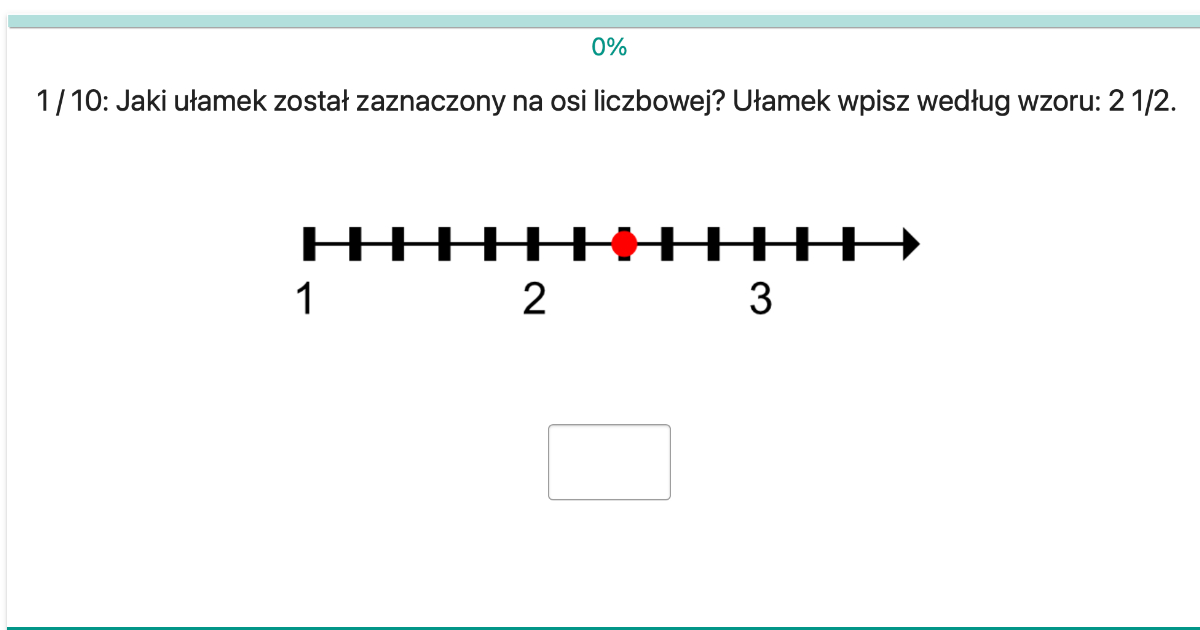
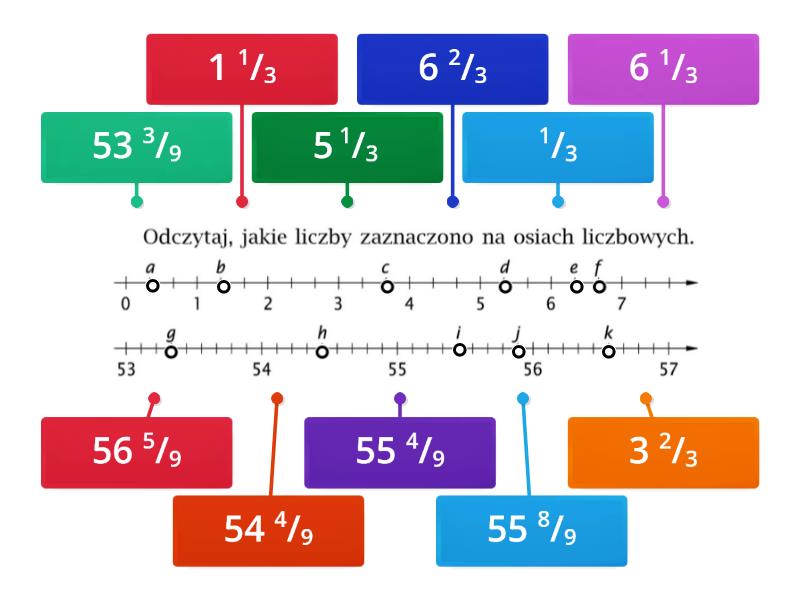
Możemy zamienić ułamek niewłaściwy (czyli taki, gdzie licznik jest większy od mianownika) na liczbę mieszaną. Liczba mieszana składa się z liczby całkowitej i ułamka właściwego. W przypadku 5/4, liczba mieszana to 1 1/4 (jeden i jedna czwarta).

Teraz wiemy, że ułamek 5/4 znajduje się pomiędzy liczbami 1 i 2. Zaczynamy od liczby 1, a następnie dzielimy odcinek między 1 a 2 na 4 równe części (bo mianownik to 4). Odliczamy 1 część od 1 (bo licznik to 1). To jest pozycja ułamka 5/4.

Dlaczego Ułamki na Osi Liczbowej Są Ważne?

Zaznaczanie ułamków na osi liczbowej to nie tylko ćwiczenie matematyczne. Pomaga nam:

• Wizualizować ułamki: Oś liczbowa pozwala nam zobaczyć, jak duże są różne ułamki i jak się mają do siebie.
• Porównywać ułamki: Możemy łatwo porównać dwa ułamki, patrząc na ich pozycje na osi liczbowej. Ułamek, który znajduje się bardziej na prawo, jest większy.
• Rozumieć relacje między ułamkami a liczbami całkowitymi: Widzimy, jak ułamki "wypełniają" przestrzeń między liczbami całkowitymi.
• Wykorzystywać ułamki w praktyce: Wiele sytuacji w życiu codziennym wymaga zrozumienia ułamków, na przykład podczas gotowania, mierzenia czy dzielenia się czymś z przyjaciółmi.

Przykłady Zastosowania w Życiu Codziennym

Pomyśl o pizzy! Jeśli podzielisz pizzę na 8 kawałków, to każdy kawałek to 1/8 pizzy. Możesz wyobrazić sobie te kawałki na osi liczbowej, od 0 (brak pizzy) do 1 (cała pizza). Dwa kawałki to 2/8 pizzy, trzy kawałki to 3/8 pizzy, i tak dalej.

Inny przykład: wyobraź sobie, że biegniesz maraton (chociaż pewnie jeszcze nie w klasie 4!). Maraton ma 42 kilometry. Jeśli przebiegniesz połowę maratonu, to przebiegniesz 1/2 z 42 kilometrów, czyli 21 kilometrów. Możesz zaznaczyć punkty na osi liczbowej, oznaczające 1/4 maratonu, 1/2 maratonu, 3/4 maratonu i cały maraton.

Jeszcze jeden przykład: w sklepie, możesz kupić 1/2 kilograma jabłek, 1/4 kilograma sera, albo 3/4 litra soku. Te ułamki kilograma i litra możesz sobie wyobrazić na osi liczbowej, od 0 do 1.

Ćwiczenia i Zabawy z Ułamkami na Osi Liczbowej

Najlepszy sposób na opanowanie ułamków na osi liczbowej to ćwiczenia! Poproś rodziców lub nauczyciela, żeby dali ci kilka ułamków do zaznaczenia. Możesz też sam wymyślać ułamki i sprawdzać, czy dobrze je zaznaczasz.

Możesz również zagrać w gry online, które uczą ułamków w interaktywny sposób. Wiele stron internetowych oferuje darmowe gry i ćwiczenia związane z ułamkami.

Proste ćwiczenia:

• Narysuj oś liczbową i zaznacz na niej ułamki: 1/2, 1/4, 3/4.
• Narysuj oś liczbową i zaznacz na niej ułamki: 1/3, 2/3.
• Narysuj oś liczbową i zaznacz na niej ułamki: 1/5, 2/5, 3/5, 4/5.
• Porównaj ułamki na osi liczbowej: który ułamek jest większy: 1/2 czy 1/4? 2/3 czy 1/3?
• Zaznacz ułamki większe od 1 na osi liczbowej: 5/4, 3/2, 7/5.

Podsumowanie

Ułamki na osi liczbowej to potężne narzędzie, które pomaga nam zrozumieć ułamki i ich relacje z liczbami całkowitymi. Dzięki wizualizacji ułamków, możemy łatwiej je porównywać, dodawać i odejmować. Pamiętaj, że im więcej ćwiczysz, tym lepiej zrozumiesz ten temat!

Nie bój się ułamków! Z odrobiną praktyki, staną się one Twoimi przyjaciółmi. Powodzenia!