Ułamki Klasa 4 Karta Pracy

Witaj w świecie ułamków! Ten artykuł został stworzony specjalnie dla uczniów klasy 4, aby pomóc Wam zrozumieć i polubić ułamki. Przygotujcie się na fascynującą podróż przez świat liczb, które nie zawsze są całe!

Co to są ułamki?

Ułamek to sposób zapisu liczby, która reprezentuje część całości. Wyobraź sobie, że masz pizzę. Jeśli podzielisz ją na 8 równych kawałków i zjesz 3 z nich, to zjadłeś 3/8 (trzy ósme) pizzy. To właśnie jest ułamek!

Budowa Ułamka

Każdy ułamek składa się z dwóch ważnych części, oddzielonych kreską ułamkową:

• Licznik: Liczba nad kreską ułamkową. Mówi nam, ile części całości mamy. W przykładzie z pizzą, licznik to 3 (bo zjedliśmy 3 kawałki).
• Mianownik: Liczba pod kreską ułamkową. Mówi nam, na ile równych części podzielona jest całość. W przykładzie z pizzą, mianownik to 8 (bo pizza była podzielona na 8 kawałków).

Zatem ułamek 3/8 czytamy jako "trzy ósme".

Rodzaje ułamków

Ułamki możemy podzielić na kilka rodzajów:

Ułamki Właściwe

Ułamek właściwy to taki ułamek, w którym licznik jest mniejszy od mianownika. Oznacza to, że ułamek reprezentuje mniej niż całą jedną całość. Przykłady: 1/2, 2/5, 7/10.

Wyobraź sobie, że masz tabliczkę czekolady podzieloną na 4 kostki. Zjadłeś jedną kostkę. Zjadłeś 1/4 tabliczki czekolady. To mniej niż cała tabliczka, prawda?

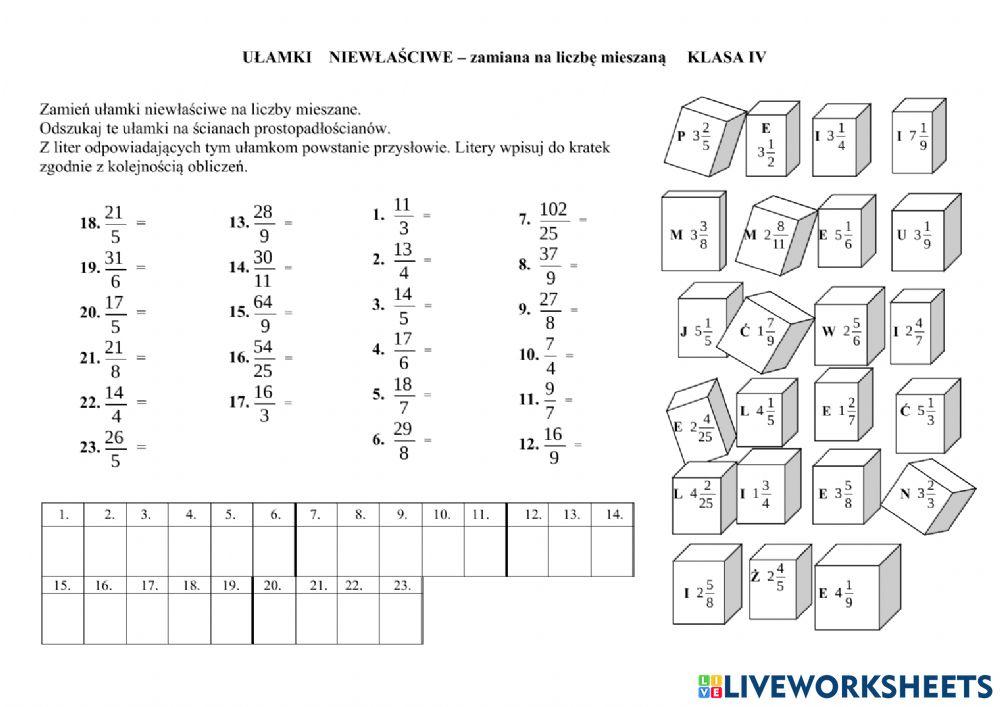
Ułamki Niewłaściwe

Ułamek niewłaściwy to taki ułamek, w którym licznik jest większy lub równy mianownikowi. Oznacza to, że ułamek reprezentuje całą jedną całość lub więcej niż jedną całość. Przykłady: 5/4, 8/8, 10/3.

Wyobraź sobie, że masz dwie pizze podzielone na 4 kawałki każda. Zjadłeś 5 kawałków. Zjadłeś 5/4 pizzy. To więcej niż jedna cała pizza!

Liczby Mieszane

Liczba mieszana składa się z liczby całkowitej i ułamka właściwego. Jest to inny sposób zapisu ułamka niewłaściwego. Przykład: 1 1/2 (jeden i jedna druga).

Wróćmy do przykładu z pizzą. Zjadłeś 5/4 pizzy. Możesz powiedzieć, że zjadłeś 1 całą pizzę i jeszcze 1/4 drugiej pizzy. Zatem 5/4 = 1 1/4.

Porównywanie ułamków

Czasami musimy porównać dwa ułamki, aby dowiedzieć się, który jest większy. Istnieje kilka sposobów na to:

Porównywanie ułamków o tym samym mianowniku

Jeśli dwa ułamki mają taki sam mianownik, to większy jest ten ułamek, który ma większy licznik. Na przykład, 3/5 jest większe od 2/5, ponieważ 3 > 2.

Wyobraź sobie, że masz dwie identyczne ciasta. Jedno ciasto podzieliłeś na 5 kawałków i zjadłeś 3 z nich. Drugie ciasto również podzieliłeś na 5 kawałków, ale zjadłeś tylko 2 z nich. Zjadłeś więcej ciasta z pierwszego ciasta, prawda?

Porównywanie ułamków o tym samym liczniku

Jeśli dwa ułamki mają taki sam licznik, to większy jest ten ułamek, który ma mniejszy mianownik. Na przykład, 1/3 jest większe od 1/4, ponieważ 3 < 4.

Wyobraź sobie, że masz dwie identyczne tabliczki czekolady. Jedną tabliczkę podzieliłeś na 3 części i zjadłeś 1 część. Drugą tabliczkę podzieliłeś na 4 części i zjadłeś 1 część. Zjadłeś więcej czekolady z tabliczki podzielonej na 3 części, prawda?

Porównywanie ułamków o różnych licznikach i mianownikach

Jeśli ułamki mają różne liczniki i mianowniki, musimy sprowadzić je do wspólnego mianownika. To oznacza, że musimy znaleźć taki mianownik, który jest podzielny przez oba mianowniki. Następnie musimy rozszerzyć ułamki tak, aby miały ten wspólny mianownik. Potem możemy porównać liczniki.

Przykład: Porównajmy ułamki 1/2 i 2/5. Wspólny mianownik dla 2 i 5 to 10. Rozszerzamy ułamki: 1/2 = 5/10 i 2/5 = 4/10. Teraz możemy porównać: 5/10 > 4/10, więc 1/2 > 2/5.

Działania na ułamkach (podstawy)

W klasie 4 zaczynamy uczyć się prostych działań na ułamkach, głównie dodawania i odejmowania ułamków o tym samym mianowniku.

Dodawanie ułamków o tym samym mianowniku

Aby dodać ułamki o tym samym mianowniku, dodajemy liczniki, a mianownik pozostaje bez zmian. Na przykład: 2/7 + 3/7 = (2+3)/7 = 5/7.

Wyobraź sobie, że masz pizzę podzieloną na 7 kawałków. Zjadłeś 2 kawałki, a potem zjadłeś jeszcze 3 kawałki. Zjadłeś łącznie 5 kawałków, czyli 5/7 pizzy.

Odejmowanie ułamków o tym samym mianowniku

Aby odjąć ułamki o tym samym mianowniku, odejmujemy liczniki, a mianownik pozostaje bez zmian. Na przykład: 5/8 - 2/8 = (5-2)/8 = 3/8.

Wyobraź sobie, że masz ciasto podzielone na 8 kawałków. Zjadłeś 5 kawałków, a potem Twój brat zjadł 2 kawałki. Zostało 3 kawałki, czyli 3/8 ciasta.

Ułamki w życiu codziennym

Ułamki są wszędzie wokół nas! Używamy ich do:

• Gotowania: Przepisy często podają składniki w ułamkach, np. 1/2 szklanki mąki.
• Mierzenia: Linijka jest podzielona na centymetry i milimetry, a milimetry to ułamki centymetra.
• Dzielenia się: Dzieląc pizzę, ciasto lub inne smakołyki, używamy ułamków.
• Odczytywania czasu: Kwadrans to 1/4 godziny.
• Zakupy: Często widzimy obniżki cen podane w ułamkach, np. "1/2 ceny".

Przykład: Mama upiekła tort i podzieliła go na 12 kawałków. Ty zjadłeś 2 kawałki, Twój brat 3 kawałki, a tata 4 kawałki. Ile tortu zjedliście łącznie? Rozwiązanie: 2/12 + 3/12 + 4/12 = 9/12. Czyli zjedliście 9/12 tortu, co można uprościć do 3/4 tortu (ponieważ 9 i 12 mają wspólny dzielnik 3).

Karta Pracy - Ćwiczenia z Ułamkami

Aby utrwalić wiedzę, wykonaj poniższe ćwiczenia:

1. Zaznacz na rysunkach podane ułamki. (Załącz rysunki podzielone na różne ilości części)
2. Wpisz brakujące liczniki lub mianowniki, aby ułamki były równe:
   • 1/2 = …/4
   • 3/5 = 6/…
3. Porównaj ułamki i wstaw odpowiedni znak: <, > lub =:
   • 1/3 … 1/4
   • 2/5 … 3/5
4. Wykonaj dodawanie lub odejmowanie ułamków:
   • 3/8 + 2/8 = …
   • 7/10 - 4/10 = …
5. Rozwiąż zadanie tekstowe: Ania miała 1/2 tabliczki czekolady. Zjadła 1/4 tabliczki. Ile tabliczki czekolady jej zostało?

Pamiętaj, ćwiczenie czyni mistrza! Im więcej będziesz ćwiczyć, tym lepiej zrozumiesz ułamki.

Podsumowanie i dalsza nauka

Gratulacje! Dotarłeś do końca tego artykułu. Mam nadzieję, że teraz lepiej rozumiesz, czym są ułamki i jak się nimi posługiwać. Ułamki to bardzo ważna część matematyki, która przydaje się w wielu sytuacjach w życiu codziennym.

Jeśli chcesz dowiedzieć się więcej o ułamkach, możesz poszukać dodatkowych materiałów w Internecie, w książkach lub zapytać swojego nauczyciela. Pamiętaj, że nauka matematyki może być świetną zabawą!

Podejmij wyzwanie! Spróbuj znaleźć ułamki w swoim otoczeniu. Policz, ile kawałków pizzy zjadłeś, ile wody wypiłeś w ciągu dnia (np. pół litra, czyli 1/2 litra) i ile czasu spędziłeś na zabawie. Powodzenia!