Ułamki I Liczby Mieszane Klasa 4 Kartkówka

Witaj w świecie ułamków i liczb mieszanych! To fundament matematyki, który otwiera drzwi do bardziej zaawansowanych koncepcji. W czwartej klasie szkoły podstawowej, zrozumienie tych zagadnień jest kluczowe. Często sprawdzane są one na kartkówkach, dlatego warto solidnie się do nich przygotować. Ten artykuł pomoże Ci zrozumieć, czym są ułamki i liczby mieszane, jak je dodawać, odejmować, a także gdzie spotykamy je w życiu codziennym.

Czym są Ułamki?

Ułamek to sposób na przedstawienie części całości. Składa się z dwóch elementów: licznika i mianownika. Licznik (liczba na górze) mówi nam, ile części bierzemy pod uwagę, a mianownik (liczba na dole) mówi nam, na ile równych części podzielona jest całość. Na przykład, w ułamku ½, 1 to licznik, a 2 to mianownik. Oznacza to, że całość została podzielona na dwie równe części, a my bierzemy jedną z nich.

Rodzaje Ułamków

Istnieją różne rodzaje ułamków, które warto znać:

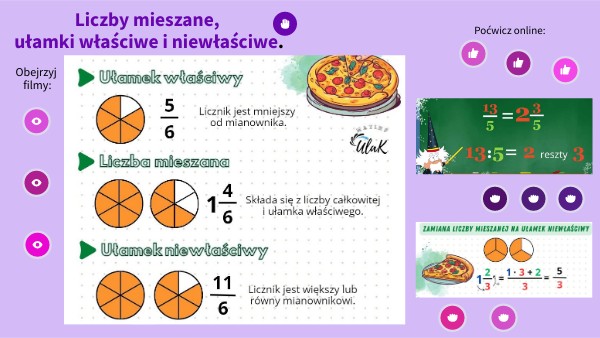
Ułamki właściwe: Licznik jest mniejszy od mianownika (np. 2/5, 7/10). Oznaczają one, że bierzemy mniej niż całą całość.
Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi (np. 5/3, 9/9). Oznaczają one, że bierzemy całą całość lub więcej niż całość.
Ułamki mieszane: Składają się z liczby całkowitej i ułamka właściwego (np. 1 1/2, 3 2/5).

Zrozumienie różnicy między tymi typami ułamków jest bardzo ważne, zwłaszcza przy wykonywaniu działań matematycznych.

Liczby Mieszane: Co to takiego?

Liczba mieszana to połączenie liczby całkowitej i ułamka właściwego. Wyobraź sobie, że masz jedną całą pizzę i jeszcze kawałek drugiej. Liczbę mieszaną można zapisać jako 1 1/4, co oznacza jedną całą pizzę i ćwierć drugiej pizzy.

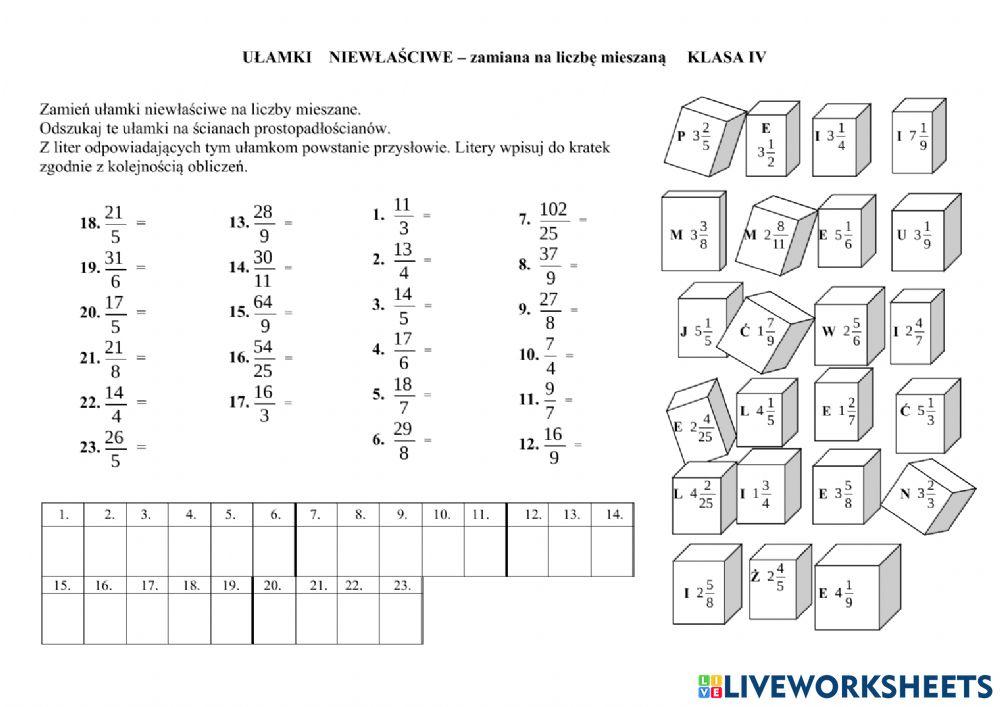
Zamiana Ułamków Niewłaściwych na Liczby Mieszane

Ułamek niewłaściwy możemy zamienić na liczbę mieszaną. Jak to zrobić? Podziel licznik przez mianownik. Wynik dzielenia to liczba całkowita, a reszta z dzielenia to licznik ułamka. Mianownik pozostaje ten sam. Na przykład, zamieńmy ułamek 7/3 na liczbę mieszaną:

Podziel 7 przez 3. Wynik to 2, a reszta to 1.
Liczba całkowita to 2.
Licznik ułamka to 1.
Mianownik ułamka to 3.

Zatem 7/3 = 2 1/3.

Zamiana Liczb Mieszanych na Ułamki Niewłaściwe

Możemy również zamienić liczbę mieszaną na ułamek niewłaściwy. Jak to zrobić? Pomnóż liczbę całkowitą przez mianownik ułamka, a następnie dodaj do tego licznik. Wynik tego działania to licznik ułamka niewłaściwego. Mianownik pozostaje ten sam. Na przykład, zamieńmy liczbę mieszaną 3 1/2 na ułamek niewłaściwy:

Pomnóż 3 przez 2. Wynik to 6.
Dodaj 6 do 1. Wynik to 7.
Licznik ułamka to 7.
Mianownik ułamka to 2.

Zatem 3 1/2 = 7/2.

Działania na Ułamkach

Zrozumienie, jak wykonywać działania na ułamkach, jest kluczowe. Oto kilka podstawowych operacji:

Dodawanie i Odejmowanie Ułamków o Tych Samych Mianownikach

Jeśli ułamki mają ten sam mianownik, dodajemy lub odejmujemy tylko liczniki. Mianownik pozostaje bez zmian. Na przykład:

2/5 + 1/5 = (2+1)/5 = 3/5
4/7 - 1/7 = (4-1)/7 = 3/7

Dodawanie i Odejmowanie Ułamków o Różnych Mianownikach

Jeśli ułamki mają różne mianowniki, musimy najpierw sprowadzić je do wspólnego mianownika. Najczęściej używamy do tego najmniejszej wspólnej wielokrotności (NWW) mianowników. Na przykład, dodajmy 1/3 i 1/4:

Znajdź NWW liczb 3 i 4. NWW(3,4) = 12.
Rozszerz ułamki do mianownika 12:
- 1/3 = (1 * 4) / (3 * 4) = 4/12
- 1/4 = (1 * 3) / (4 * 3) = 3/12
Dodaj ułamki: 4/12 + 3/12 = 7/12

Dodawanie i Odejmowanie Liczb Mieszanych

Podczas dodawania i odejmowania liczb mieszanych, możemy postępować na dwa sposoby:

Sposób 1: Oddzielnie dodajemy (lub odejmujemy) liczby całkowite i ułamki, a następnie upraszczamy wynik.
Sposób 2: Zamieniamy liczby mieszane na ułamki niewłaściwe, wykonujemy działanie, a następnie zamieniamy wynik z powrotem na liczbę mieszaną.

Na przykład, dodajmy 2 1/4 i 1 1/2:

Sposób 1:

Dodajemy liczby całkowite: 2 + 1 = 3
Dodajemy ułamki: 1/4 + 1/2 = 1/4 + 2/4 = 3/4
Wynik: 3 3/4

Sposób 2:

Zamieniamy liczby mieszane na ułamki niewłaściwe: 2 1/4 = 9/4, 1 1/2 = 3/2
Sprowadzamy do wspólnego mianownika: 3/2 = 6/4
Dodajemy ułamki: 9/4 + 6/4 = 15/4
Zamieniamy na liczbę mieszaną: 15/4 = 3 3/4

Ułamki w Życiu Codziennym

Ułamki i liczby mieszane są obecne w wielu aspektach naszego życia. Oto kilka przykładów:

Gotowanie: Przepisy często wymagają użycia ułamków, np. ½ szklanki mąki, ¼ łyżeczki soli.
Mierzenie: Ułamki i liczby mieszane są używane do mierzenia długości, wagi, czasu, np. 2 ½ metra materiału, ¾ kilograma jabłek.
Dzielenie się: Kiedy dzielimy pizzę, ciasto lub inne przedmioty na równe części, używamy ułamków.
Czas: Kwadrans to ¼ godziny, pół godziny to ½ godziny.

Wyobraź sobie, że pieczesz ciasto. Przepis wymaga 1 1/2 szklanki mąki. Potrzebujesz również ¼ łyżeczki proszku do pieczenia i ¾ szklanki cukru. Ułamki są nieodzowne w gotowaniu!

Inny przykład: Dzielisz się pizzą z trzema przyjaciółmi. Każda osoba dostaje ¼ pizzy. Ty również jesz ¼ pizzy. Razem zjedliście 4 * ¼ = 1 całą pizzę.

Przykładowe Zadania na Kartkówce

Oto kilka typowych zadań, które mogą pojawić się na kartkówce z ułamków i liczb mieszanych:

Zamień ułamek niewłaściwy na liczbę mieszaną: np. 11/4
Zamień liczbę mieszaną na ułamek niewłaściwy: np. 2 2/3
Dodaj ułamki: np. 1/5 + 2/5
Odejmij ułamki: np. 5/8 - 1/8
Dodaj ułamki o różnych mianownikach: np. 1/2 + 1/3
Odejmij ułamki o różnych mianownikach: np. 2/3 - 1/4
Dodaj liczby mieszane: np. 1 1/2 + 2 1/4
Odejmij liczby mieszane: np. 3 2/5 - 1 1/5
Porównaj ułamki: np. Czy 2/3 jest większe, mniejsze, czy równe 3/5?
Rozwiąż zadanie tekstowe z użyciem ułamków.

Wskazówki i Triki

Ćwicz regularnie: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz ułamki.
Zwracaj uwagę na szczegóły: Sprawdź, czy ułamki mają te same mianowniki przed dodaniem lub odjęciem.
Upraszczaj ułamki: Zawsze staraj się uprościć ułamek do najmniejszej postaci.
Używaj wizualizacji: Narysuj diagramy lub użyj przedmiotów, aby lepiej zrozumieć, jak działają ułamki.
Sprawdzaj odpowiedzi: Po rozwiązaniu zadania, zawsze sprawdź, czy odpowiedź ma sens.

Podsumowanie

Zrozumienie ułamków i liczb mieszanych jest bardzo ważne w matematyce. Dzięki temu artykułowi powinieneś lepiej rozumieć, czym są ułamki, jak je dodawać, odejmować i zamieniać. Pamiętaj, że ćwiczenie czyni mistrza. Regularnie rozwiązuj zadania, a bez problemu poradzisz sobie na kartkówce z ułamków! Powodzenia!