Ułamki Dziesiętne Klasa 6 Karta Pracy

Czy ułamki dziesiętne spędzają Ci sen z powiek? Czy Twoje dziecko w szóstej klasie ma trudności z ich zrozumieniem? Nie jesteś sam! Ułamki dziesiętne to fundament matematyki, a ich solidne opanowanie jest kluczowe dla dalszego sukcesu w szkole. Wiele dzieci (i dorosłych!) zmaga się z tym tematem. Ale spokojnie, jesteśmy tu, żeby pomóc. Ten artykuł to Twój przewodnik po ułamkach dziesiętnych, specjalnie przygotowany dla rodziców i uczniów klasy 6, z naciskiem na efektywne karty pracy.

Wyobraź sobie, że pieczesz ciasto z dzieckiem. Przepis wymaga 0,5 kg mąki. Czy wiesz, jak to odmierzyć? To właśnie umiejętność operowania ułamkami dziesiętnymi w praktyce! Zrozumienie, jak zamieniać ułamki zwykłe na dziesiętne, dodawać, odejmować, mnożyć i dzielić – to wszystko jest niezbędne nie tylko w szkole, ale i w życiu codziennym.

Dlaczego ułamki dziesiętne są takie ważne?

Ułamki dziesiętne są wszechobecne. Spotykamy je w sklepach (ceny produktów), w kuchni (przepisy), w sporcie (wyniki), a nawet w nauce (pomiary). Zrozumienie ich pozwala na swobodne poruszanie się w świecie liczb i rozwiązywanie problemów, które wydają się skomplikowane, gdy nie mamy tej wiedzy.

Według badań przeprowadzonych przez Instytut Badań Edukacyjnych (IBE), uczniowie, którzy wcześnie opanują operacje na ułamkach dziesiętnych, mają większe szanse na sukces w dalszej edukacji matematycznej, w tym w algebrze i geometrii. Dlatego tak ważne jest, aby poświęcić temu tematowi odpowiednią uwagę.

Ułamki dziesiętne - Krok po kroku

Zacznijmy od podstaw. Ułamek dziesiętny to ułamek, którego mianownik jest potęgą liczby 10 (10, 100, 1000 itd.). Rozdzielamy część całkowitą od części ułamkowej przecinkiem. Na przykład, 3,14 to ułamek dziesiętny, gdzie 3 to część całkowita, a 14 to część ułamkowa.

Zapis ułamków dziesiętnych

Każda cyfra po przecinku ma swoje miejsce: dziesiąte, setne, tysięczne itd. Na przykład, w liczbie 5,27:

5 to jedności
2 to dziesiąte
7 to setne

Ważne jest, aby pamiętać o zerach na końcu ułamka dziesiętnego. Dodanie zera na końcu nie zmienia wartości ułamka. Na przykład, 0,5 = 0,50 = 0,500.

Zamiana ułamków zwykłych na dziesiętne i odwrotnie

Zamiana ułamka zwykłego na dziesiętny: jeśli to możliwe, rozszerz ułamek zwykły tak, aby jego mianownik był potęgą liczby 10. Na przykład, chcemy zamienić 1/2 na ułamek dziesiętny. Rozszerzamy ułamek przez 5: 1/2 = 5/10 = 0,5.

Jeśli nie da się łatwo rozszerzyć ułamka, możemy podzielić licznik przez mianownik. Na przykład, aby zamienić 1/4 na ułamek dziesiętny, dzielimy 1 przez 4, co daje 0,25.

Zamiana ułamka dziesiętnego na zwykły: zapisujemy ułamek dziesiętny jako ułamek zwykły z mianownikiem 10, 100, 1000 itd. w zależności od ilości cyfr po przecinku. Następnie, jeśli to możliwe, skracamy ułamek. Na przykład, 0,75 = 75/100 = 3/4.

Działania na ułamkach dziesiętnych

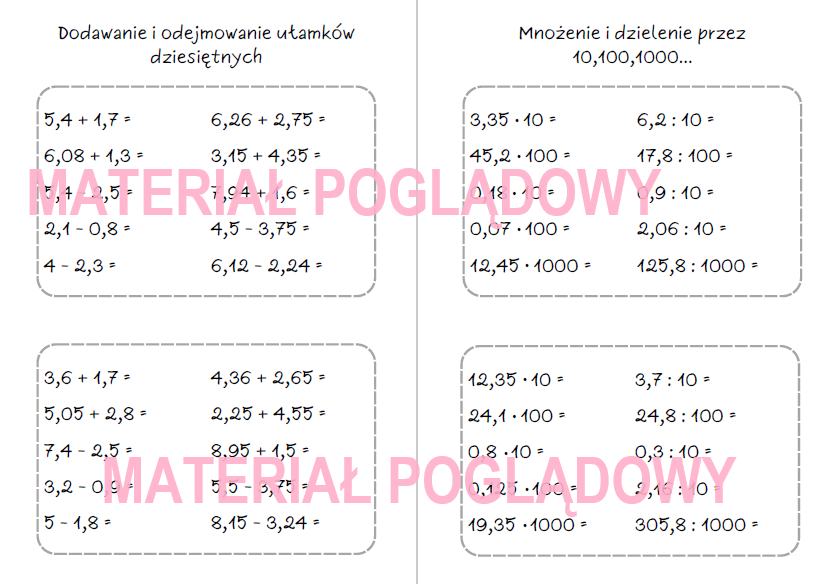
Dodawanie i odejmowanie: Najważniejsze jest, aby doprowadzić ułamki do wspólnego rzędu, czyli wyrównać ilość cyfr po przecinku, dodając zera. Następnie dodajemy lub odejmujemy jak liczby całkowite, pamiętając o przecinku.

Przykład: 2,3 + 1,45 = 2,30 + 1,45 = 3,75

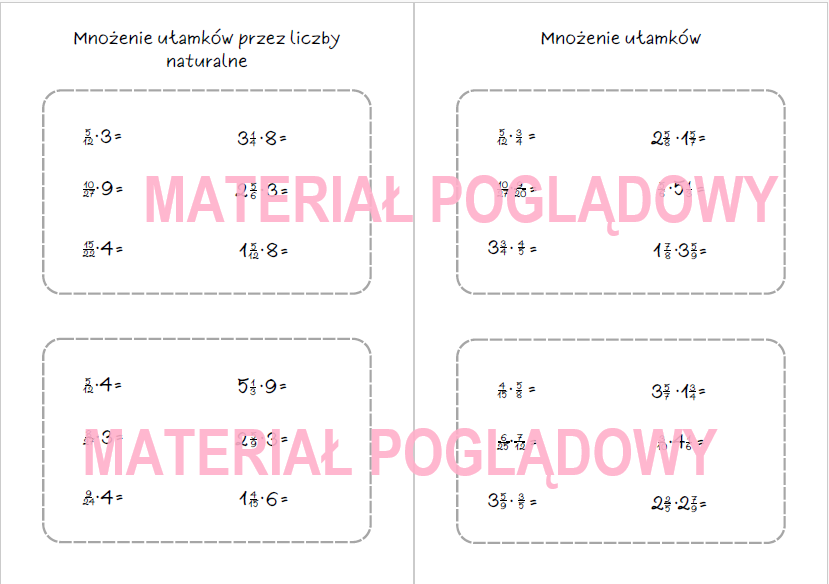
Mnożenie: Mnożymy ułamki dziesiętne jak liczby całkowite, a następnie przesuwamy przecinek w wyniku o tyle miejsc w lewo, ile łącznie jest cyfr po przecinku w mnożonych liczbach.

Przykład: 1,5 * 0,2 = 0,30 (1 cyfra po przecinku w 1,5 + 1 cyfra po przecinku w 0,2 = 2 cyfry po przecinku w wyniku)

Dzielenie: Dzielenie ułamków dziesiętnych jest nieco bardziej skomplikowane. Przede wszystkim, przesuwamy przecinek w dzielniku o tyle miejsc w prawo, aby dzielnik stał się liczbą całkowitą. Następnie przesuwamy przecinek w dzielnej o tyle samo miejsc w prawo. Jeśli brakuje cyfr, dopisujemy zera. Potem dzielimy jak liczby całkowite.

Przykład: 4,8 : 1,2 = 48 : 12 = 4

Karty Pracy – Klucz do sukcesu

Karty pracy to nieocenione narzędzie w nauce ułamków dziesiętnych. Umożliwiają one praktyczne ćwiczenie poznanych zagadnień i utrwalanie wiedzy. Dobrze przygotowane karty pracy powinny zawierać różnorodne zadania: od prostych przykładów na dodawanie i odejmowanie, po bardziej skomplikowane zadania tekstowe, które wymagają logicznego myślenia i zastosowania wiedzy w praktyce.

Jak efektywnie wykorzystywać karty pracy?

Rozpocznij od prostych zadań: Upewnij się, że dziecko dobrze rozumie podstawowe zasady.
Stopniowo zwiększaj poziom trudności: Pozwól dziecku rozwijać umiejętności krok po kroku.
Skup się na zrozumieniu, a nie tylko na wyniku: Pytaj dziecko, jak rozwiązało zadanie i dlaczego.
Wykorzystaj zadania tekstowe: Pomagają one zrozumieć praktyczne zastosowanie ułamków dziesiętnych.
Sprawdzaj wyniki i omawiaj błędy: To doskonała okazja do wyjaśnienia wątpliwości i utrwalenia wiedzy.
Wykorzystaj gry i zabawy: Nauka nie musi być nudna! Istnieje wiele gier i zabaw edukacyjnych, które pomagają w nauce ułamków dziesiętnych.

Gdzie znaleźć dobre karty pracy? Wiele stron internetowych oferuje darmowe materiały edukacyjne. Warto poszukać kart pracy dostosowanych do poziomu klasy 6, które obejmują wszystkie omawiane zagadnienia.

Praktyczne wskazówki dla rodziców

Oto kilka praktycznych wskazówek, które pomogą Ci wesprzeć dziecko w nauce ułamków dziesiętnych:

Bądź cierpliwy: Nauka wymaga czasu i wysiłku. Nie zrażaj się, jeśli dziecko ma trudności.
Stwórz pozytywną atmosferę: Nauka powinna być przyjemnością, a nie stresem.
Połącz naukę z zabawą: Wykorzystaj gry i zabawy edukacyjne.
Wykorzystaj sytuacje z życia codziennego: Pokaż dziecku, jak ułamki dziesiętne są używane w praktyce.
Chwal za postępy: Motywacja jest kluczowa!

Pamiętaj, że Twoje zaangażowanie jest niezwykle ważne. Poświęć czas na wspólne rozwiązywanie zadań, odpowiadaj na pytania i wspieraj dziecko w trudnych momentach. Z Twoją pomocą ułamki dziesiętne przestaną być straszne!

Przykładowe zadania na kartach pracy

Oto kilka przykładów zadań, które mogą pojawić się na kartach pracy dla klasy 6:

Zamień ułamki zwykłe na dziesiętne: 1/4, 3/5, 7/10, 2/25.
Zamień ułamki dziesiętne na zwykłe: 0,25, 0,8, 0,125, 0,6.
Oblicz: 2,5 + 3,7, 5,8 - 1,2, 1,5 * 0,3, 4,8 : 1,6.
Rozwiąż zadanie tekstowe: Ania kupiła 2,5 kg jabłek po 3,20 zł za kilogram. Ile zapłaciła?
Porównaj ułamki dziesiętne: 0,7 i 0,75, 1,2 i 1,19, 0,05 i 0,5.

Kluczem do sukcesu jest regularna praktyka i systematyczne rozwiązywanie zadań. Wykorzystuj karty pracy, gry edukacyjne i sytuacje z życia codziennego, aby nauka była przyjemna i efektywna. Pamiętaj, że cierpliwość i wsparcie ze strony rodziców są niezwykle ważne.

Zrozumienie ułamków dziesiętnych to inwestycja w przyszłość Twojego dziecka. Dobre opanowanie tego tematu otworzy mu drogę do sukcesu w dalszej edukacji matematycznej i w życiu codziennym. Więc nie zwlekaj, zacznij już dziś! Powodzenia!