Ułamek W Którym Licznik Jest Mniejszy Od Mianownika

Ułamki są ważną częścią matematyki i spotykamy je na co dzień, choćby dzieląc pizzę, odmierzając składniki do ciasta, czy sprawdzając, ile czasu minęło od początku lekcji. W tym artykule skupimy się na szczególnym rodzaju ułamków: tych, w których licznik jest mniejszy od mianownika. Zrozumienie tych ułamków jest kluczowe do dalszego zgłębiania tajników matematyki.

Zacznijmy od podstaw. Czym właściwie jest ułamek?

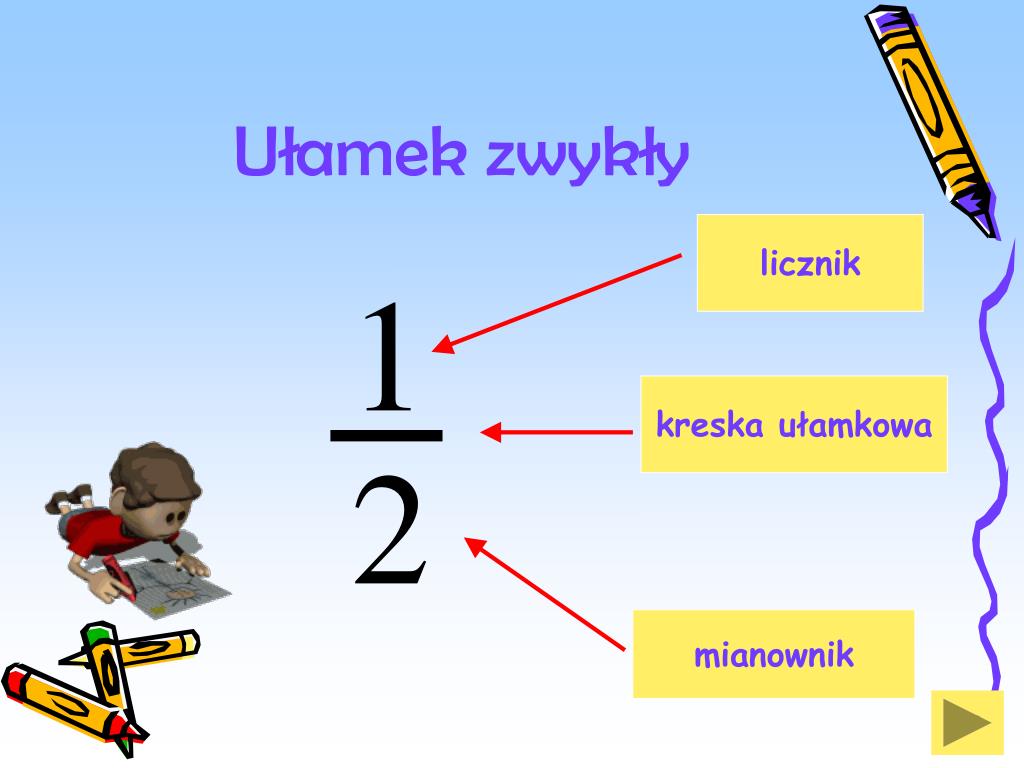
Ułamek reprezentuje część całości. Składa się z dwóch elementów: licznika i mianownika, oddzielonych kreską ułamkową.

Mianownik: Mówi nam, na ile równych części całość została podzielona. Znajduje się pod kreską ułamkową.
Licznik: Mówi nam, ile z tych części bierzemy pod uwagę. Znajduje się nad kreską ułamkową.

Na przykład, w ułamku 3/4 (czytamy "trzy czwarte"), mianownik to 4, co oznacza, że całość została podzielona na cztery równe części. Licznik to 3, co oznacza, że bierzemy pod uwagę trzy z tych czterech części. Wyobraźmy sobie pizzę podzieloną na cztery kawałki. Jeśli zjemy trzy z tych kawałków, to zjemy 3/4 pizzy.

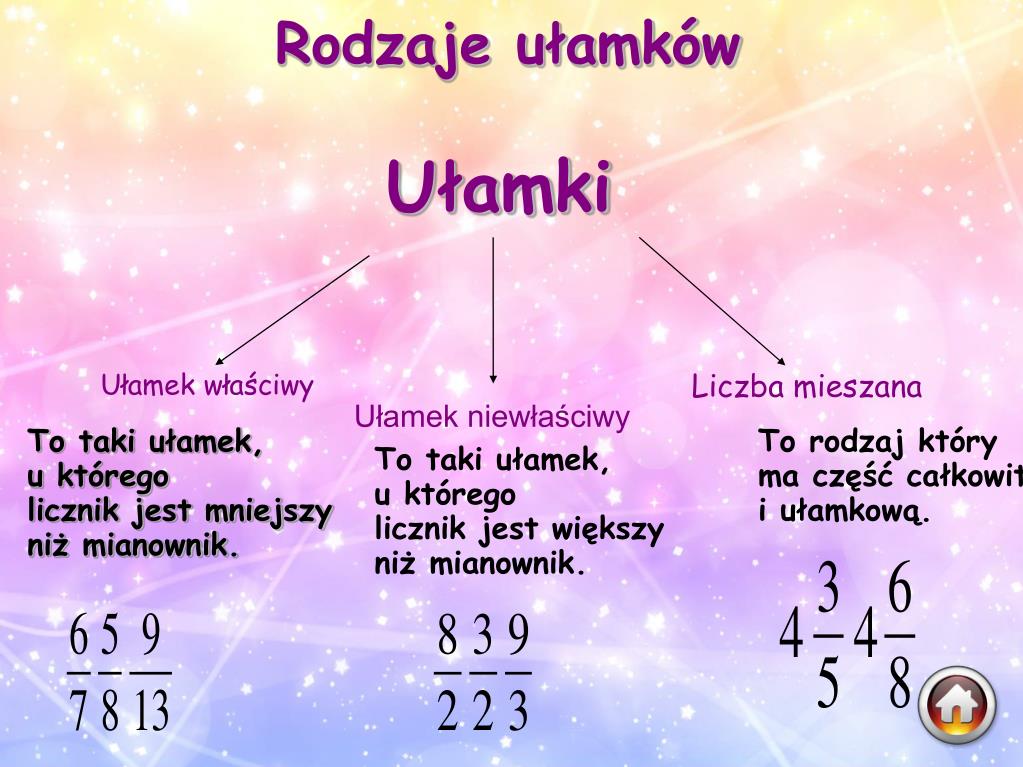
Teraz przejdźmy do sedna: ułamki, w których licznik jest mniejszy od mianownika. Ułamki te mają specjalną nazwę: ułamki właściwe.

Ułamek właściwy to taki ułamek, w którym licznik jest mniejszy od mianownika. Inaczej mówiąc, bierzemy mniej części niż tych, na które całość została podzielona.

Przykłady ułamków właściwych:

1/2 (jedna druga) – bierzemy jeden kawałek z dwóch.
2/5 (dwie piąte) – bierzemy dwa kawałki z pięciu.
7/10 (siedem dziesiątych) – bierzemy siedem kawałków z dziesięciu.
15/32 (piętnaście trzydziestych drugich) – bierzemy piętnaście kawałków z trzydziestu dwóch.
99/100 (dziewięćdziesiąt dziewięć setnych) - bierzemy dziewięćdziesiąt dziewięć kawałków ze stu.

Cechy ułamków właściwych:

Najważniejszą cechą ułamków właściwych jest to, że ich wartość jest zawsze mniejsza od 1. Oznacza to, że reprezentują one mniej niż całą jednostkę. Jeśli masz 1/2 ciastka, to masz mniej niż całe ciastko. Analogicznie, jeśli masz 3/4 szklanki wody, to masz mniej niż pełną szklankę.

Ułamki niewłaściwe:

Dla kontrastu, warto wspomnieć o ułamkach, w których licznik jest większy lub równy mianownikowi. Nazywamy je ułamkami niewłaściwymi. Przykłady to 5/4, 7/3, czy 8/8. Ułamki niewłaściwe mają wartość większą lub równą 1. Na przykład, 5/4 oznacza, że mamy więcej niż całą pizzę – jedną całą pizzę i jeszcze jeden kawałek z kolejnej.

Praktyczne zastosowania ułamków właściwych:

Ułamki właściwe są używane w wielu sytuacjach w życiu codziennym. Oto kilka przykładów:

Gotowanie: Przepisy często wymagają użycia ułamkowych ilości składników, takich jak 1/2 szklanki mąki, 1/4 łyżeczki soli, czy 2/3 filiżanki cukru.
Mierzenie: Ułamki są powszechnie używane do mierzenia długości, wagi i objętości. Na przykład, możemy powiedzieć, że coś ma 1/2 metra długości lub waży 3/4 kilograma.
Pieniądze: Grosze to ułamki złotego. Na przykład, 50 groszy to 1/2 złotego (0.50 zł).
Czas: Minuty to ułamki godziny. Na przykład, 30 minut to 1/2 godziny. Kwadranse to 1/4 godziny.
Planowanie: Możemy powiedzieć, że spędzimy 1/3 dnia w szkole, a 2/5 dnia na zabawie.

Rozwiązywanie zadań z ułamkami właściwymi:

Rozwiązywanie zadań z ułamkami właściwymi wymaga zrozumienia ich reprezentacji i relacji. Możemy dodawać, odejmować, mnożyć i dzielić ułamki właściwe, przestrzegając odpowiednich zasad. Na przykład, aby dodać dwa ułamki o tym samym mianowniku, dodajemy liczniki, a mianownik pozostaje bez zmian: 1/5 + 2/5 = 3/5.

Podsumowanie:

Ułamki właściwe to ułamki, w których licznik jest mniejszy od mianownika. Reprezentują one mniej niż całą jednostkę i są szeroko stosowane w życiu codziennym, od gotowania po mierzenie i planowanie. Zrozumienie ułamków właściwych jest fundamentalne dla opanowania matematyki i radzenia sobie z różnymi sytuacjami, w których konieczne jest operowanie częściami całości. Pamiętaj, że praktyka czyni mistrza, więc ćwicz rozwiązywanie zadań z ułamkami właściwymi, a staną się one dla Ciebie łatwe i zrozumiałe.

Jak rozpoznawać i porównywać ułamki właściwe?

Rozpoznawanie ułamków właściwych jest proste: wystarczy sprawdzić, czy licznik jest mniejszy od mianownika. Porównywanie ułamków właściwych może być nieco bardziej skomplikowane, ale istnieje kilka prostych metod.

Porównywanie ułamków o tym samym mianowniku:

Jeśli dwa ułamki mają ten sam mianownik, łatwo je porównać: większy jest ten ułamek, który ma większy licznik. Na przykład, 3/7 jest większe od 2/7, ponieważ 3 > 2. Wyobraźmy sobie tort podzielony na 7 kawałków. Zjedzenie 3 kawałków tortu to więcej niż zjedzenie 2 kawałków.

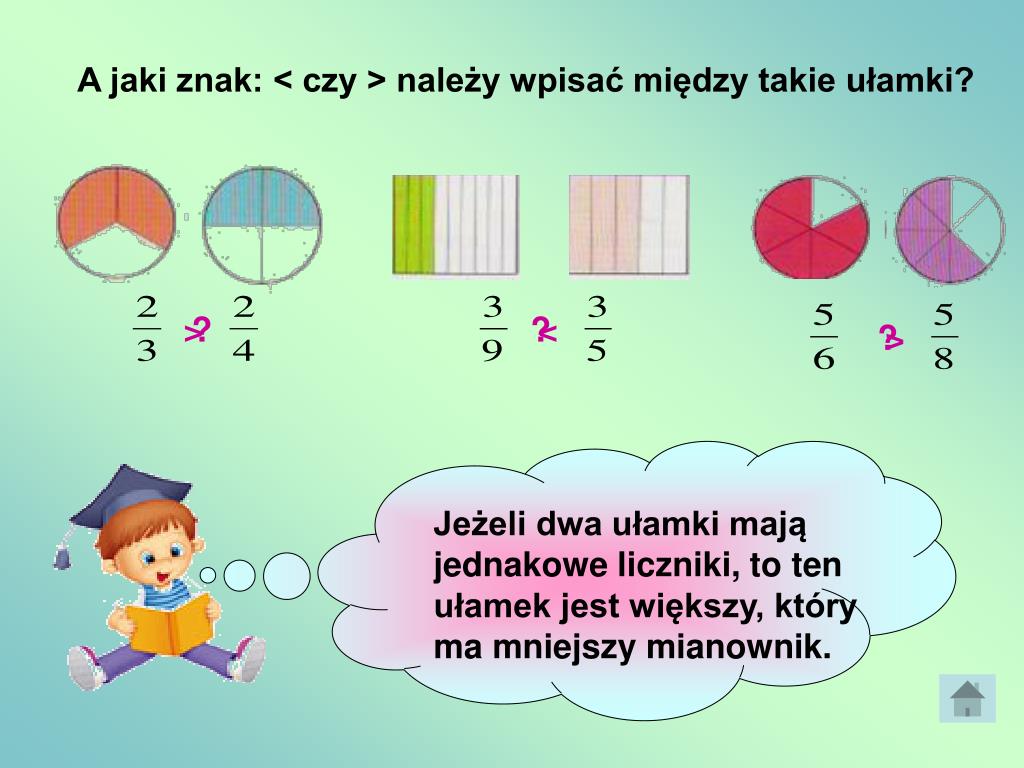
Porównywanie ułamków o różnych mianownikach:

Jeśli ułamki mają różne mianowniki, musimy je najpierw sprowadzić do wspólnego mianownika. Oznacza to znalezienie takiego mianownika, który jest wielokrotnością obu mianowników. Najczęściej używamy najmniejszej wspólnej wielokrotności (NWW).

Na przykład, aby porównać 1/3 i 2/5, musimy znaleźć NWW dla 3 i 5. NWW(3, 5) = 15. Następnie zamieniamy oba ułamki na ułamki o mianowniku 15:

1/3 = (1 * 5) / (3 * 5) = 5/15
2/5 = (2 * 3) / (5 * 3) = 6/15

Teraz możemy łatwo porównać ułamki: 5/15 jest mniejsze od 6/15, więc 1/3 jest mniejsze od 2/5.

Inne metody porównywania:

Porównywanie do 1/2: Możemy porównać oba ułamki do 1/2. Jeśli jeden ułamek jest większy od 1/2, a drugi mniejszy, to łatwo określić, który jest większy. Na przykład, 3/5 jest większe od 1/2 (bo 3 jest większe od połowy 5), a 2/7 jest mniejsze od 1/2 (bo 2 jest mniejsze od połowy 7). Zatem 3/5 jest większe od 2/7.
Zamiana na ułamki dziesiętne: Możemy zamienić ułamki zwykłe na ułamki dziesiętne i porównać liczby dziesiętne. Na przykład, 1/4 = 0.25, a 1/2 = 0.5. Zatem 1/4 jest mniejsze od 1/2.

Zrozumienie i opanowanie tych technik pozwoli Ci swobodnie porównywać ułamki właściwe i używać ich w różnych sytuacjach.