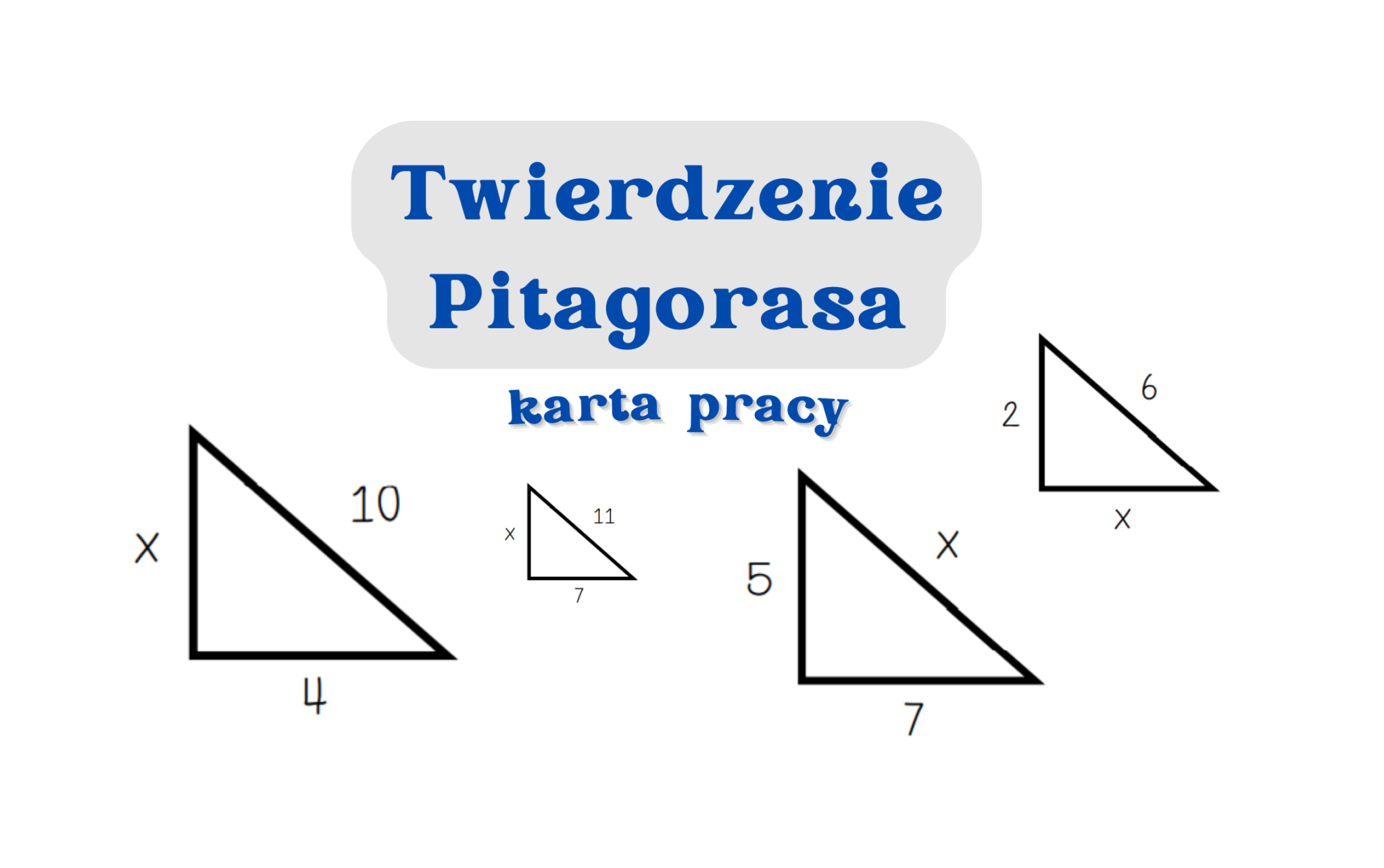
Twierdzenie Pitagorasa Zadania Klasa 8

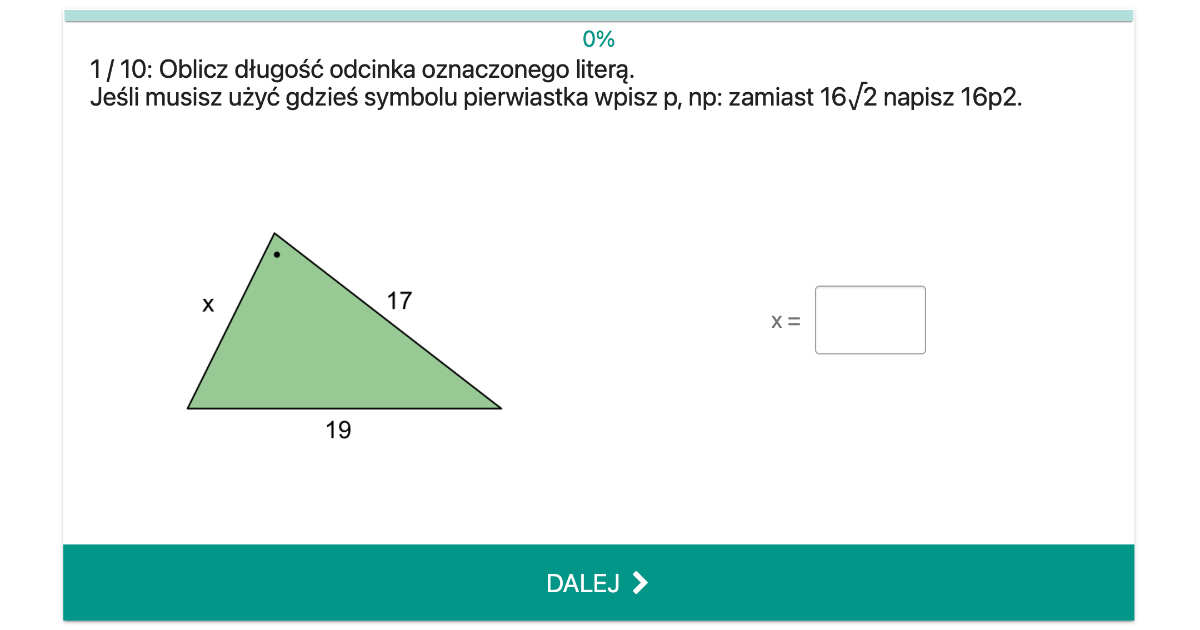
Zmagasz się z Twierdzeniem Pitagorasa w ósmej klasie? Nie martw się! Wiele osób uważa je za jedno z trudniejszych zagadnień matematycznych, ale zrozumienie go wcale nie musi być koszmarem. Ten artykuł jest dla Ciebie - przeprowadzimy Cię przez podstawy, pokażemy praktyczne zastosowania i nauczymy, jak rozwiązywać zadania krok po kroku. Przygotuj się na podróż do świata trójkątów prostokątnych, kwadratów i potęg, która okaże się o wiele prostsza, niż myślisz!

Czym właściwie jest Twierdzenie Pitagorasa?

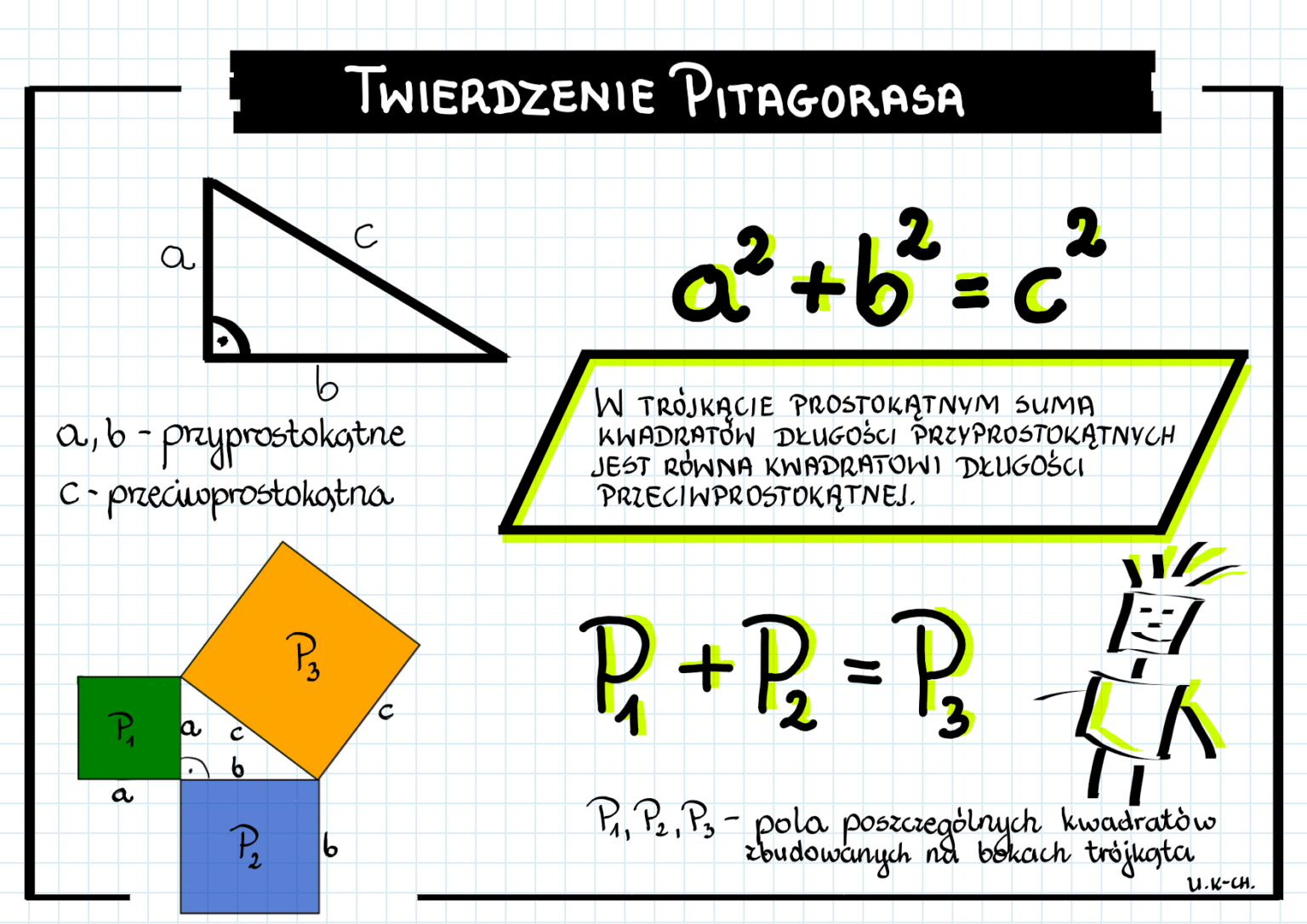
Najpierw, rozprawmy się z definicją. Twierdzenie Pitagorasa opisuje fundamentalną zależność między długościami boków trójkąta prostokątnego. Brzmi strasznie? Spokojnie! Przypomnijmy sobie, czym jest trójkąt prostokątny. To taki trójkąt, który posiada jeden kąt prosty (90 stopni). Bok naprzeciwko tego kąta nazywamy przeciwprostokątną (oznaczamy najczęściej jako 'c'), a dwa pozostałe boki to przyprostokątne (oznaczamy jako 'a' i 'b').

Twierdzenie Pitagorasa mówi, że:

a² + b² = c²

Czyli: suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Proste, prawda?

Dlaczego to działa?

Choć sama formuła jest krótka i zwięzła, jej udowodnienie wymaga pewnej wiedzy geometrycznej. Istnieje wiele dowodów Twierdzenia Pitagorasa, niektóre z nich są bardzo proste i oparte na polu powierzchni figur geometrycznych. Spróbuj wyobrazić sobie kwadrat zbudowany na każdej z przyprostokątnych i przeciwprostokątnej. Twierdzenie Pitagorasa mówi, że suma pól kwadratów zbudowanych na przyprostokątnych jest równa polu kwadratu zbudowanego na przeciwprostokątnej.

Zastosowania Twierdzenia Pitagorasa

Twierdzenie Pitagorasa to nie tylko sucha teoria! Ma ono mnóstwo zastosowań w życiu codziennym i w różnych dziedzinach nauki. Oto kilka przykładów:

• Budownictwo: Architekci i inżynierowie wykorzystują to twierdzenie do obliczania długości przekątnych, wysokości budynków, czy też do precyzyjnego wyznaczania kątów prostych.
• Nawigacja: Kapitanowie statków i piloci samolotów używają Twierdzenia Pitagorasa do obliczania odległości i kursów.
• Stolarstwo: Stolarze wykorzystują to twierdzenie do tworzenia mebli o idealnych kątach prostych i do obliczania długości potrzebnych elementów.
• Informatyka: W grafice komputerowej Twierdzenie Pitagorasa jest używane do obliczania odległości między punktami na ekranie.

Jak widzisz, Twierdzenie Pitagorasa jest niezwykle wszechstronne!

Przykłady zadań i ich rozwiązywanie

Teraz przejdźmy do konkretów. Jak rozwiązywać zadania z wykorzystaniem Twierdzenia Pitagorasa?

Zadanie 1: Obliczanie długości przeciwprostokątnej

Treść: Dany jest trójkąt prostokątny o przyprostokątnych długości 3 cm i 4 cm. Oblicz długość przeciwprostokątnej.

Rozwiązanie:

1. Zapisujemy wzór: a² + b² = c²
2. Podstawiamy dane: 3² + 4² = c²
3. Obliczamy kwadraty: 9 + 16 = c²
4. Dodajemy: 25 = c²
5. Wyciągamy pierwiastek kwadratowy: c = √25 = 5

Odpowiedź: Długość przeciwprostokątnej wynosi 5 cm.

Zadanie 2: Obliczanie długości przyprostokątnej

Treść: Dany jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 13 cm, a jedna z przyprostokątnych ma długość 5 cm. Oblicz długość drugiej przyprostokątnej.

Rozwiązanie:

1. Zapisujemy wzór: a² + b² = c²
2. Podstawiamy dane: 5² + b² = 13²
3. Obliczamy kwadraty: 25 + b² = 169
4. Przenosimy 25 na prawą stronę: b² = 169 - 25
5. Odejmujemy: b² = 144
6. Wyciągamy pierwiastek kwadratowy: b = √144 = 12

Odpowiedź: Długość drugiej przyprostokątnej wynosi 12 cm.

Zadanie 3: Zastosowanie w życiu codziennym

Treść: Drabina o długości 5 metrów jest oparta o ścianę budynku. Dolny koniec drabiny znajduje się 3 metry od ściany. Na jakiej wysokości znajduje się górny koniec drabiny?

Rozwiązanie:

Wyobraź sobie trójkąt prostokątny, gdzie drabina jest przeciwprostokątną, odległość drabiny od ściany to jedna przyprostokątna, a wysokość, na jakiej znajduje się drabina, to druga przyprostokątna.

1. Zapisujemy wzór: a² + b² = c²
2. Podstawiamy dane: 3² + b² = 5²
3. Obliczamy kwadraty: 9 + b² = 25
4. Przenosimy 9 na prawą stronę: b² = 25 - 9
5. Odejmujemy: b² = 16
6. Wyciągamy pierwiastek kwadratowy: b = √16 = 4

Odpowiedź: Górny koniec drabiny znajduje się na wysokości 4 metrów.

Wskazówki i triki

• Rysuj! Zawsze rysuj sobie schemat trójkąta prostokątnego, żeby lepiej zrozumieć, co masz dane, a co musisz obliczyć.
• Sprawdzaj jednostki! Upewnij się, że wszystkie długości są podane w tej samej jednostce (np. centymetry, metry).
• Ćwicz! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz Twierdzenie Pitagorasa i nauczysz się je stosować w różnych sytuacjach.
• Zapamiętaj popularne trójki pitagorejskie! To zestawy liczb całkowitych spełniające Twierdzenie Pitagorasa (np. 3, 4, 5; 5, 12, 13; 8, 15, 17). Znajomość tych trójek może znacznie przyspieszyć rozwiązywanie zadań.

Częste błędy i jak ich unikać

• Pomylenie przyprostokątnych z przeciwprostokątną: Zawsze upewnij się, która strona jest przeciwprostokątną (ta naprzeciwko kąta prostego).
• Błędne podstawienie do wzoru: Upewnij się, że podstawiasz odpowiednie wartości do wzoru a² + b² = c².
• Zapominanie o wyciągnięciu pierwiastka: Po obliczeniu wartości a², b² lub c², pamiętaj o wyciągnięciu pierwiastka kwadratowego, żeby otrzymać długość boku.

Podsumowanie

Twierdzenie Pitagorasa może wydawać się skomplikowane na początku, ale z odrobiną praktyki i zrozumieniem podstaw, stanie się Twoim sprzymierzeńcem w rozwiązywaniu zadań matematycznych i problemów z życia codziennego. Pamiętaj, że kluczem do sukcesu jest zrozumienie definicji, poznanie zastosowań i regularne ćwiczenia. Nie zrażaj się trudnościami i korzystaj z dostępnych zasobów, takich jak ten artykuł, podręczniki i materiały online. Powodzenia!