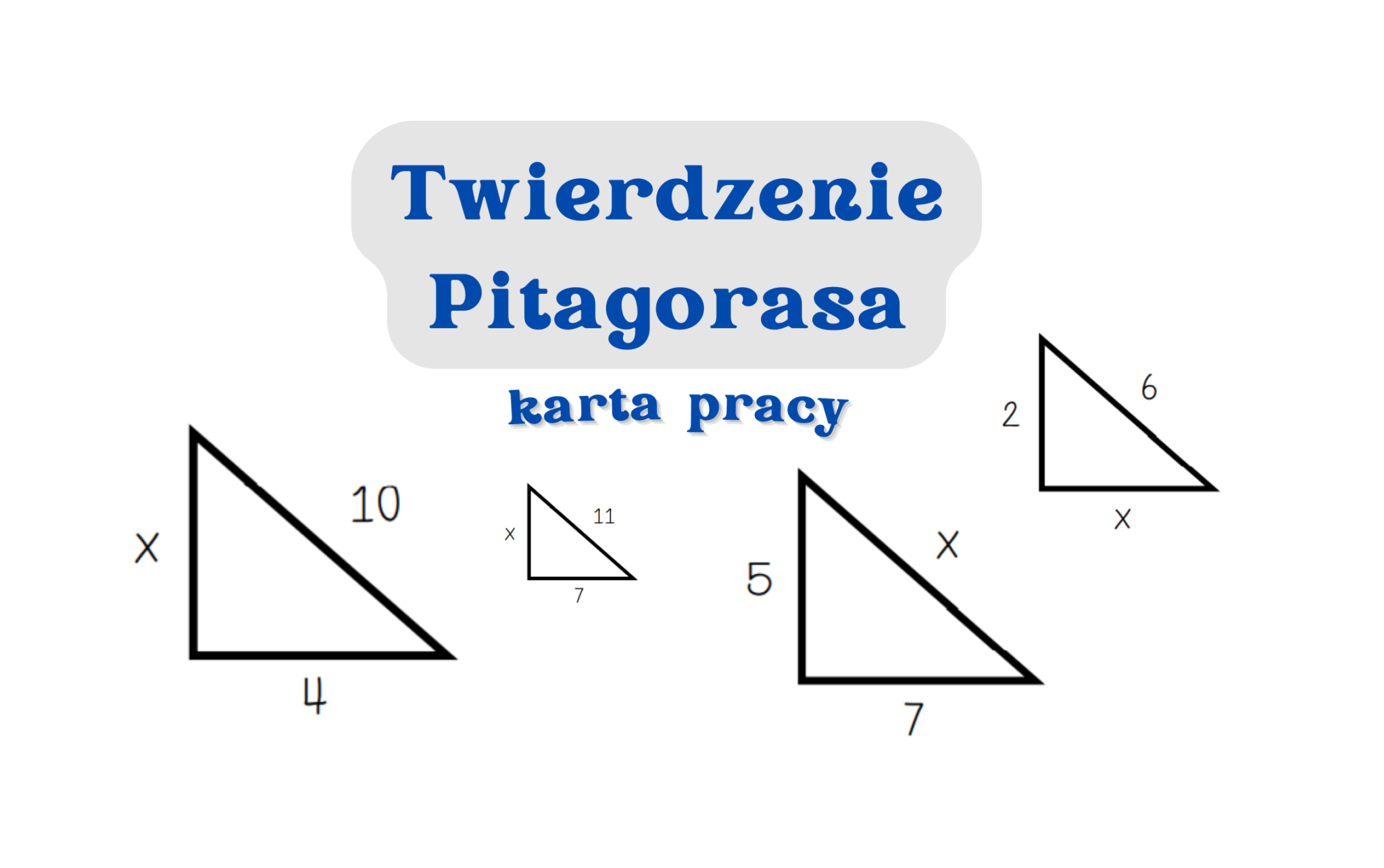
Twierdzenie Pitagorasa Zadania Klasa 7

Hej wszystkim! Dziś zanurzymy się w świat jednego z najbardziej znanych i lubianych twierdzeń w matematyce – w Twierdzenie Pitagorasa! Nie martwcie się, brzmi groźnie, ale w rzeczywistości jest proste i bardzo przydatne. Specjalnie dla uczniów 7 klasy, ale i dla każdego, kto chce odświeżyć sobie tę wiedzę. Przygotujcie się na przygodę pełną trójkątów i kwadratów!

Co to jest Twierdzenie Pitagorasa?

Twierdzenie Pitagorasa opisuje zależność między długościami boków w trójkącie prostokątnym. Ale zanim przejdziemy do sedna, rozłóżmy to na czynniki pierwsze:

Trójkąt prostokątny – co to takiego?

Wyobraź sobie trójkąt. Zwykły trójkąt, prawda? Teraz, wyobraź sobie, że jeden z jego kątów jest kątem prostym. Kąt prosty to taki kąt, który ma 90 stopni – możesz go zobaczyć w rogu kartki papieru, w rogu ściany, albo w miejscu gdzie stykają się dwie proste linie tworząc idealny kąt "L". Trójkąt, który ma taki kąt, nazywamy trójkątem prostokątnym.

Boki trójkąta prostokątnego

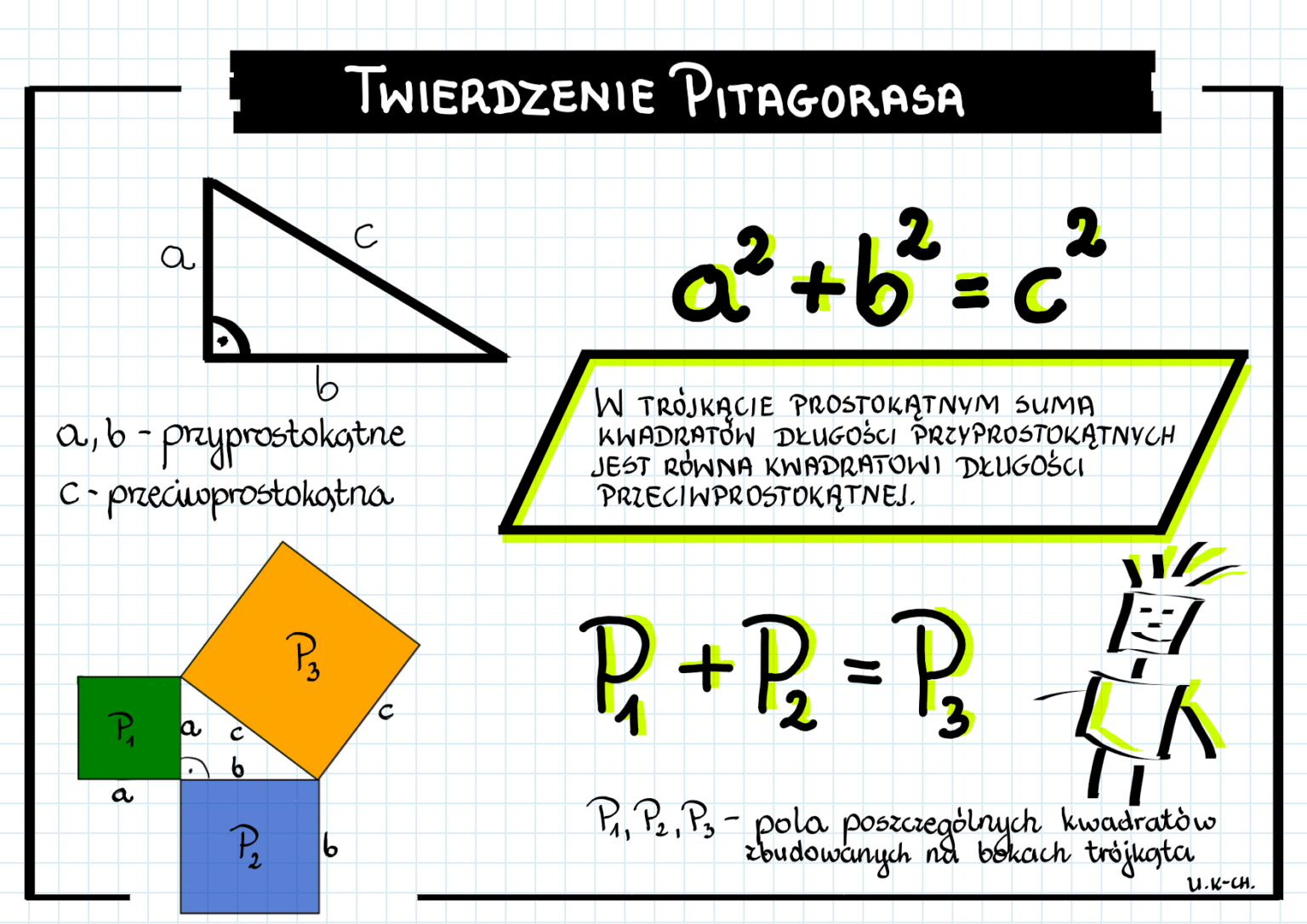
Trójkąt prostokątny ma trzy boki. Dwa z nich, które tworzą kąt prosty, nazywamy przyprostokątnymi. Wyobraź sobie, że to nogi, które "podtrzymują" kąt prosty. Trzeci bok, który leży naprzeciwko kąta prostego (i jest jednocześnie najdłuższym bokiem), nazywamy przeciwprostokątną.

Teraz, najważniejsza informacja: Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Brzmi skomplikowanie? Spokojnie, zaraz to uprościmy.

Formuła Twierdzenia Pitagorasa

Matematycznie, Twierdzenie Pitagorasa zapisujemy tak:

a² + b² = c²

Gdzie:

a i b to długości przyprostokątnych
c to długość przeciwprostokątnej

Zastanówmy się, co to oznacza. a² oznacza "a do kwadratu", czyli a * a. Podobnie b² to b * b, a c² to c * c. Mówiąc prościej, jeśli narysujemy kwadrat na każdej z przyprostokątnych i przeciwprostokątnej, to suma pól kwadratów narysowanych na przyprostokątnych będzie równa polu kwadratu narysowanego na przeciwprostokątnej. Spróbuj to sobie zwizualizować, to bardzo pomaga!

Przykłady z życia codziennego

Twierdzenie Pitagorasa nie jest tylko suchą teorią. Ma mnóstwo zastosowań w prawdziwym życiu! Oto kilka przykładów:

Budownictwo: Wyobraź sobie budowniczego, który chce sprawdzić, czy ściana jest idealnie pionowa (czy tworzy kąt prosty z podłogą). Może on użyć Twierdzenia Pitagorasa do obliczenia długości przekątnej ściany i porównania jej z oczekiwaną wartością.
Nawigacja: Żeglarz płynie na wschód przez 3 kilometry, a potem na północ przez 4 kilometry. Jak daleko jest od punktu startu w linii prostej? Możemy potraktować jego trasę jako dwie przyprostokątne trójkąta prostokątnego, a odległość od punktu startu jako przeciwprostokątną. Zatem: 3² + 4² = c², czyli 9 + 16 = c², czyli 25 = c². Stąd c = 5. Żeglarz jest 5 kilometrów od punktu startu.
Projektowanie: Architekt projektuje rampę dla osób niepełnosprawnych. Musi obliczyć długość rampy (przeciwprostokątną), znając wysokość, na jaką rampa ma się wznosić (jedna przyprostokątna) i odległość poziomą, jaką rampa ma pokonywać (druga przyprostokątna).

Rozwiązywanie zadań z Twierdzeniem Pitagorasa

Czas na praktykę! Rozwiążmy kilka przykładowych zadań:

Przykład 1:

W trójkącie prostokątnym jedna przyprostokątna ma długość 6 cm, a druga 8 cm. Oblicz długość przeciwprostokątnej.

Rozwiązanie:

Podstawiamy wartości do wzoru: a² + b² = c².
Czyli: 6² + 8² = c²
Wykonujemy obliczenia: 36 + 64 = c²
Stąd: 100 = c²
Pierwiastkujemy obie strony równania: √100 = √c²
Otrzymujemy: c = 10 cm

Odpowiedź: Długość przeciwprostokątnej wynosi 10 cm.

Przykład 2:

Przeciwprostokątna trójkąta prostokątnego ma długość 13 cm, a jedna z przyprostokątnych ma długość 5 cm. Oblicz długość drugiej przyprostokątnej.

Rozwiązanie:

Podstawiamy wartości do wzoru: a² + b² = c².
Czyli: 5² + b² = 13²
Wykonujemy obliczenia: 25 + b² = 169
Przenosimy 25 na prawą stronę równania (odejmujemy 25 od obu stron): b² = 169 - 25
Stąd: b² = 144
Pierwiastkujemy obie strony równania: √b² = √144
Otrzymujemy: b = 12 cm

Odpowiedź: Długość drugiej przyprostokątnej wynosi 12 cm.

Podsumowanie

Twierdzenie Pitagorasa jest fundamentalnym twierdzeniem w geometrii, które opisuje relację między bokami trójkąta prostokątnego. Pamiętaj o wzorze: a² + b² = c², gdzie a i b to przyprostokątne, a c to przeciwprostokątna. Spróbuj rozwiązywać jak najwięcej zadań, aby dobrze opanować tę wiedzę. Powodzenia!