Twierdzenie Pitagorasa Sprawdzian Klasa 7

Cześć wszystkim! Zbliża się sprawdzian z Twierdzenia Pitagorasa w 7 klasie? Nie martw się! Ten artykuł pomoże Ci zrozumieć to zagadnienie krok po kroku. Rozłożymy to na czynniki pierwsze, wyjaśnimy wszystkie ważne pojęcia i pokażemy przykłady z życia wzięte. Po przeczytaniu tego artykułu, sprawdzian z Pitagorasa będzie dla Ciebie bułką z masłem!

Co to jest Twierdzenie Pitagorasa?

Twierdzenie Pitagorasa to fundamentalne twierdzenie geometrii, które opisuje związek między długościami boków w trójkącie prostokątnym. Brzmi strasznie? Spokojnie, zaraz wszystko stanie się jasne.

Ale zanim przejdziemy do samego twierdzenia, musimy zrozumieć, czym jest trójkąt prostokątny.

Trójkąt Prostokątny: Podstawowe Pojęcia

Trójkąt prostokątny to trójkąt, który ma jeden kąt prosty, czyli kąt o mierze 90 stopni. Wyobraź sobie róg kartki papieru – to jest kąt prosty!

W trójkącie prostokątnym wyróżniamy trzy boki:

• Przeciwprostokątna: Jest to najdłuższy bok trójkąta prostokątnego. Zawsze leży naprzeciwko kąta prostego.
• Przyprostokątne: Są to dwa pozostałe boki trójkąta prostokątnego. One tworzą kąt prosty.

Wyobraź sobie, że trzymasz kartkę papieru w kształcie trójkąta prostokątnego. Najdłuższy bok (przeciwprostokątna) jest wtedy jak "dach" trójkąta, a dwa pozostałe boki (przyprostokątne) to "ściany".

Wzór na Twierdzenie Pitagorasa

Teraz, kiedy już wiemy, co to jest trójkąt prostokątny, możemy przejść do samego Twierdzenia Pitagorasa. Mówi ono, że:

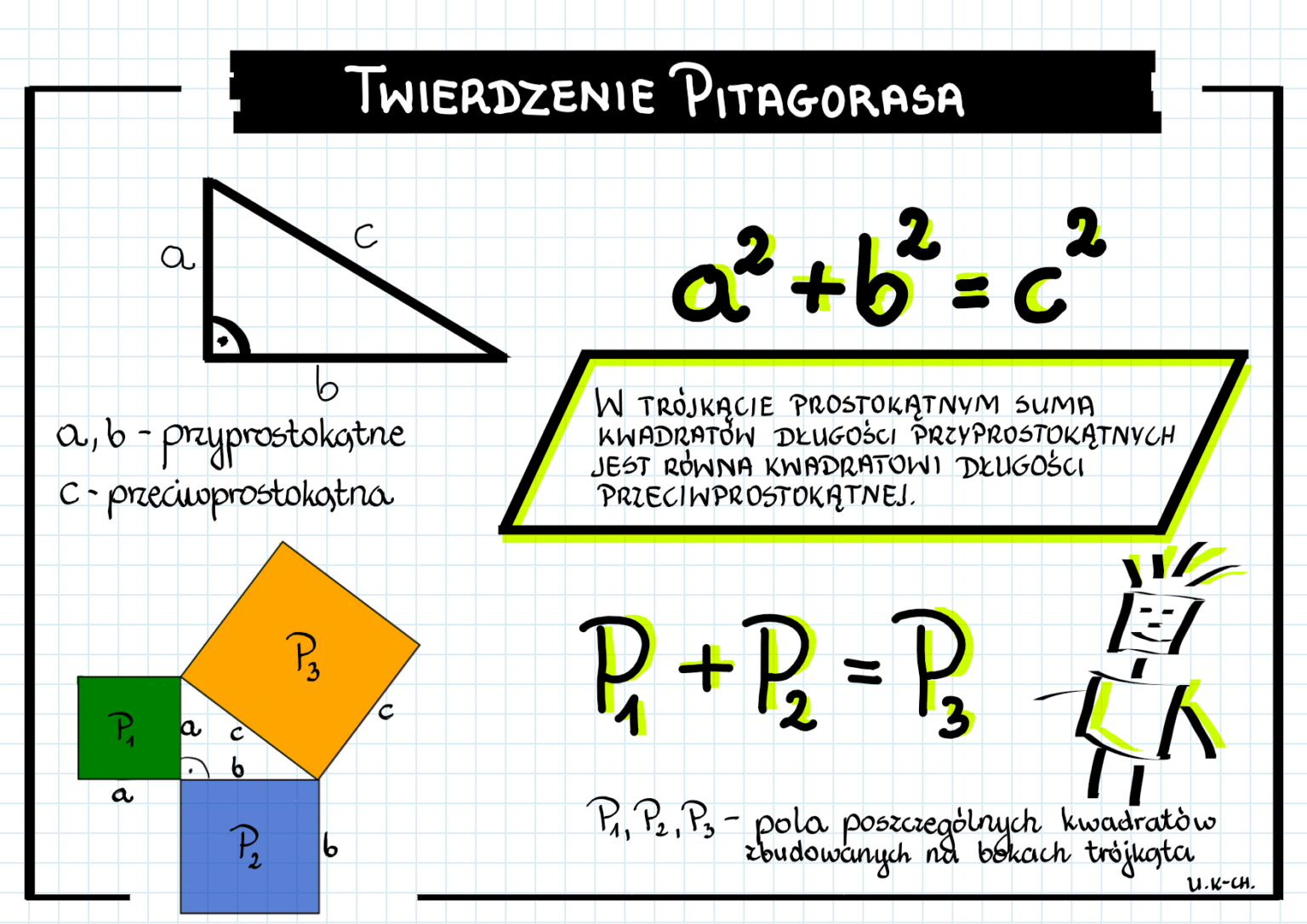
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.

Brzmi skomplikowanie? Zapiszmy to za pomocą wzoru:

a² + b² = c²

Gdzie:

• a i b to długości przyprostokątnych
• c to długość przeciwprostokątnej

Innymi słowy, jeśli znasz długości dwóch boków trójkąta prostokątnego (dwóch przyprostokątnych lub jednej przyprostokątnej i przeciwprostokątnej), możesz obliczyć długość trzeciego boku!

Przykłady Zastosowania Twierdzenia Pitagorasa

Teraz zobaczymy, jak to działa w praktyce. Pokażemy kilka przykładów, które pomogą Ci zrozumieć, jak stosować Twierdzenie Pitagorasa.

Przykład 1: Obliczanie Długości Przeciwprostokątnej

Mamy trójkąt prostokątny, w którym przyprostokątne mają długości 3 cm i 4 cm. Chcemy obliczyć długość przeciwprostokątnej.

Zastosujmy wzór: a² + b² = c²

1. Podstawiamy dane: 3² + 4² = c²
2. Obliczamy kwadraty: 9 + 16 = c²
3. Dodajemy: 25 = c²
4. Wyciągamy pierwiastek kwadratowy z obu stron: √25 = c
5. Otrzymujemy: c = 5

Zatem, przeciwprostokątna ma długość 5 cm.

Przykład 2: Obliczanie Długości Przyprostokątnej

Mamy trójkąt prostokątny, w którym przeciwprostokątna ma długość 13 cm, a jedna z przyprostokątnych ma długość 5 cm. Chcemy obliczyć długość drugiej przyprostokątnej.

Zastosujmy wzór: a² + b² = c²

1. Podstawiamy dane: 5² + b² = 13²
2. Obliczamy kwadraty: 25 + b² = 169
3. Odejmujemy 25 od obu stron: b² = 169 - 25
4. Otrzymujemy: b² = 144
5. Wyciągamy pierwiastek kwadratowy z obu stron: √144 = b
6. Otrzymujemy: b = 12

Zatem, druga przyprostokątna ma długość 12 cm.

Twierdzenie Pitagorasa w Życiu Codziennym

Może się wydawać, że Twierdzenie Pitagorasa to tylko abstrakcyjny wzór matematyczny, ale w rzeczywistości ma wiele zastosowań w życiu codziennym.

• Budownictwo: Architekci i inżynierowie używają Twierdzenia Pitagorasa do obliczania długości dachów, ścian i innych elementów konstrukcyjnych.
• Nawigacja: Kapitanowie statków i piloci samolotów używają go do wyznaczania odległości i kursów.
• Stolarstwo: Stolarze używają go do tworzenia kątów prostych i zapewnienia, że meble są stabilne.
• Sport: Na przykład, obliczanie długości przekątnej boiska do piłki nożnej.

Wyobraź sobie, że chcesz zawiesić półkę na ścianie i upewnić się, że jest ona równo. Możesz użyć kątownika, który tworzy kąt prosty, a Twierdzenie Pitagorasa pomoże Ci obliczyć, czy przekątna półki ma odpowiednią długość, aby była idealnie prosta!

Wskazówki na Sprawdzian z Twierdzenia Pitagorasa

Oto kilka wskazówek, które pomogą Ci przygotować się do sprawdzianu z Twierdzenia Pitagorasa:

• Zapamiętaj wzór: a² + b² = c². To podstawa!
• Rozróżniaj boki trójkąta prostokątnego: Pamiętaj, że przeciwprostokątna to najdłuższy bok i leży naprzeciwko kąta prostego.
• Ćwicz rozwiązywanie zadań: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz, jak stosować Twierdzenie Pitagorasa.
• Zrozumienie zamiast zapamiętywania: Staraj się zrozumieć, dlaczego Twierdzenie Pitagorasa działa, zamiast tylko uczyć się go na pamięć.
• Sprawdzaj swoje odpowiedzi: Upewnij się, że Twoje odpowiedzi mają sens w kontekście zadania. Na przykład, długość boku nie może być ujemna.

Pamiętaj, że najważniejsze to regularna nauka i rozwiązywanie zadań. Nie zostawiaj wszystkiego na ostatnią chwilę. Jeśli masz jakieś pytania, nie wstydź się zapytać nauczyciela lub kolegów.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć Twierdzenie Pitagorasa. Powodzenia na sprawdzianie!