Twierdzenie Pitagorasa Kartkówka Klasa 8

Witajcie, ósmoklasiści! Przed nami kartkówka z Twierdzenia Pitagorasa. Nie martwcie się! Rozłóżmy to twierdzenie na czynniki pierwsze, żebyście na kartkówce błyszczeli. Przygotujcie się na podróż po trójkątach prostokątnych, gdzie boki tańczą w kwadratach, a wszystko to sprowadza się do prostej, ale potężnej zależności.

Czym jest Twierdzenie Pitagorasa?

Twierdzenie Pitagorasa to fundamentalna zasada geometrii, która opisuje związek między bokami trójkąta prostokątnego. Pamiętajcie, trójkąt prostokątny to taki, który ma jeden kąt prosty – czyli kąt o mierze 90 stopni. Wyobraźcie sobie róg kartki albo kąt prosty, który tworzy ściana z podłogą.

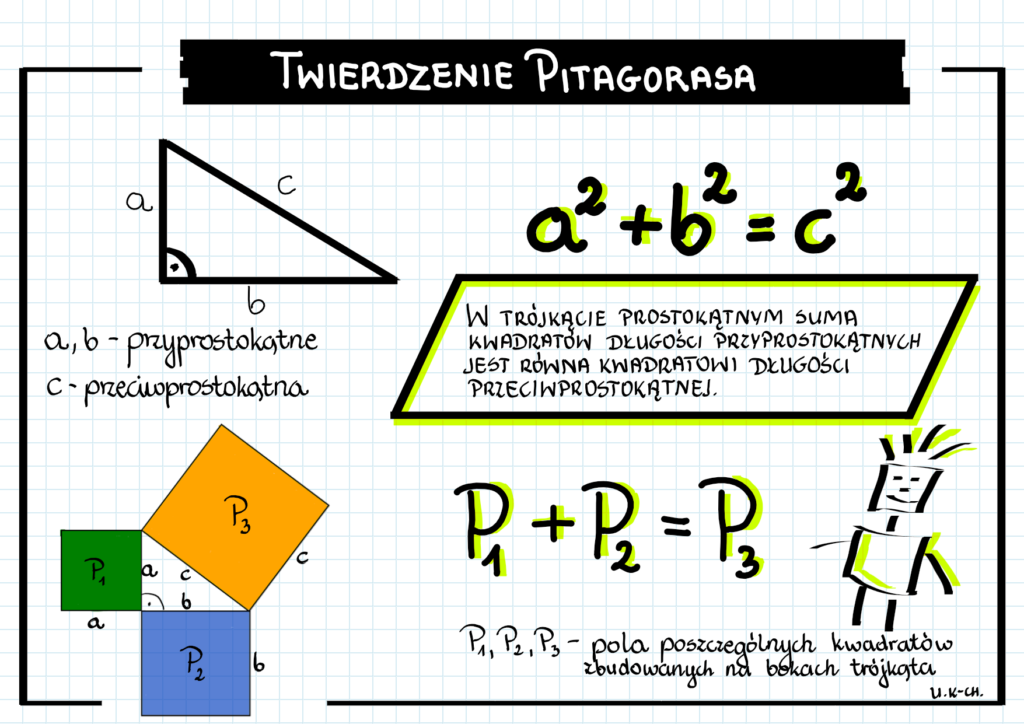
W trójkącie prostokątnym wyróżniamy dwa boki przylegające do kąta prostego – nazywamy je przyprostokątnymi. Oznaczmy je literami a i b. Bok leżący naprzeciw kąta prostego to przeciwprostokątna, którą oznaczamy literą c. Jest to zawsze najdłuższy bok w trójkącie prostokątnym.

Teraz dochodzimy do samego twierdzenia: Suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Brzmi skomplikowanie? Spokojnie! Zapisujemy to wzorem:

a² + b² = c²

Proste, prawda? Zobaczmy, jak to działa w praktyce.

Wyobraźnia przestrzenna: Kwadraty na bokach

Wyobraźcie sobie, że na każdym boku trójkąta prostokątnego zbudowaliśmy kwadrat. Pole kwadratu zbudowanego na przyprostokątnej a to a², a na przyprostokątnej b to b². Twierdzenie Pitagorasa mówi nam, że jeśli dodamy te dwa pola (a² + b²), to otrzymamy pole kwadratu zbudowanego na przeciwprostokątnej c (c²).

Pomyślcie o puzzlach. Dwa mniejsze kwadraty (zbudowane na przyprostokątnych) idealnie wypełnią większy kwadrat (zbudowany na przeciwprostokątnej). To właśnie wizualizacja twierdzenia Pitagorasa! Poszukajcie w internecie animacji, które to pokazują – obraz mówi więcej niż tysiąc słów.

Przykłady z życia wzięte

Gdzie możemy spotkać Twierdzenie Pitagorasa w życiu codziennym? Okazuje się, że bardzo często!

Budownictwo: Robotnicy używają go, aby upewnić się, że kąty budynków są idealnie proste. Wyobraźcie sobie, że budujecie fundamenty domu. Musicie mieć pewność, że rogi są pod kątem 90 stopni. Możecie zmierzyć boki trójkąta (na przykład 3 metry i 4 metry) i sprawdzić, czy przeciwprostokątna ma 5 metrów. Jeśli tak, kąt jest prosty! (3² + 4² = 9 + 16 = 25 = 5²)
Nawigacja: Piloci i kapitanowie statków wykorzystują je do obliczania odległości i kursów. Jeśli statek płynie na wschód przez 30 km, a następnie na północ przez 40 km, możemy użyć Twierdzenia Pitagorasa, aby obliczyć, jak daleko jest od punktu początkowego w linii prostej. (30² + 40² = 900 + 1600 = 2500. Pierwiastek z 2500 to 50, więc statek jest 50 km od punktu startu).
Stolarstwo: Stolarze używają go do tworzenia mebli, które mają idealne kąty proste.
Sport: Podczas gry w baseball, zawodnik rzuca piłkę z pierwszej bazy do trzeciej. Możemy obliczyć odległość, jaką piłka pokonała, używając Twierdzenia Pitagorasa.

Jak rozwiązywać zadania?

Teraz najważniejsze – jak rozwiązywać zadania na kartkówce. Oto kilka wskazówek:

Zidentyfikuj trójkąt prostokątny: Upewnij się, że masz do czynienia z trójkątem prostokątnym. Szukaj kąta prostego (oznaczonego kwadracikiem).
Oznacz boki: Zidentyfikuj przyprostokątne (a i b) oraz przeciwprostokątną (c). Pamiętaj, przeciwprostokątna leży naprzeciw kąta prostego.
Zastosuj wzór: Wstaw dane do wzoru a² + b² = c².
Rozwiąż równanie: Oblicz nieznaną wartość. Często będziesz musiał obliczyć pierwiastek kwadratowy.
Pamiętaj o jednostkach: Upewnij się, że jednostki długości są takie same (np. wszystkie w centymetrach lub metrach).

Przykładowe zadanie

Przyprostokątne trójkąta prostokątnego mają długości 6 cm i 8 cm. Oblicz długość przeciwprostokątnej.

Mamy trójkąt prostokątny.
a = 6 cm, b = 8 cm, c = ?
6² + 8² = c²
36 + 64 = c² => 100 = c² => c = √100 = 10 cm
Odpowiedź: Przeciwprostokątna ma długość 10 cm.

Kilka dodatkowych wskazówek

Rysuj schematy: Nawet jeśli zadanie nie wymaga rysunku, narysuj go! Pomoże Ci to zwizualizować problem.
Sprawdzaj wyniki: Upewnij się, że Twój wynik ma sens. Przeciwprostokątna zawsze musi być najdłuższym bokiem.
Ćwicz, ćwicz, ćwicz: Rozwiąż jak najwięcej zadań. Im więcej ćwiczysz, tym pewniej będziesz się czuł na kartkówce.

Pamiętajcie, że Twierdzenie Pitagorasa jest jak klucz, który otwiera drzwi do wielu ciekawych zagadnień matematycznych. Powodzenia na kartkówce! Wierzę w Was!