Twierdzenie Pitagorasa I Jego Zastosowanie

Drodzy nauczyciele matematyki!

Zapraszam do lektury artykułu, który ma na celu pomóc Wam w efektywnym i angażującym nauczaniu Twierdzenia Pitagorasa oraz jego zastosowań. To jedno z fundamentalnych pojęć w geometrii, które, dobrze wytłumaczone, otwiera przed uczniami drzwi do głębszego zrozumienia matematyki i jej praktycznego zastosowania.

Wprowadzenie do Twierdzenia Pitagorasa

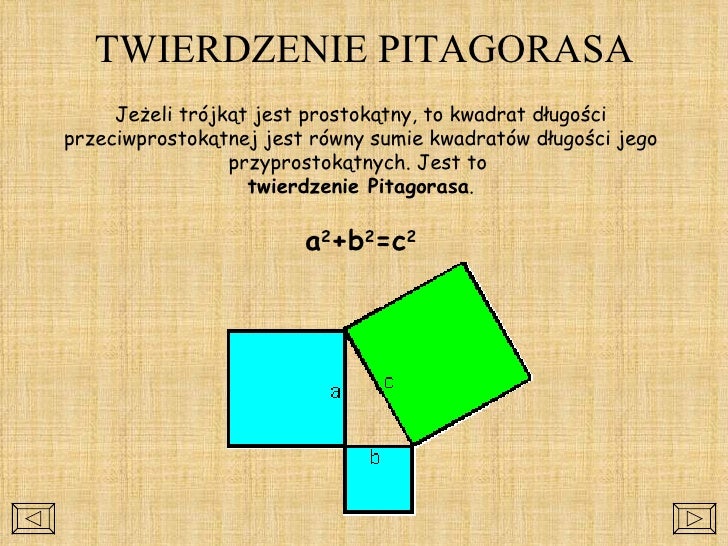
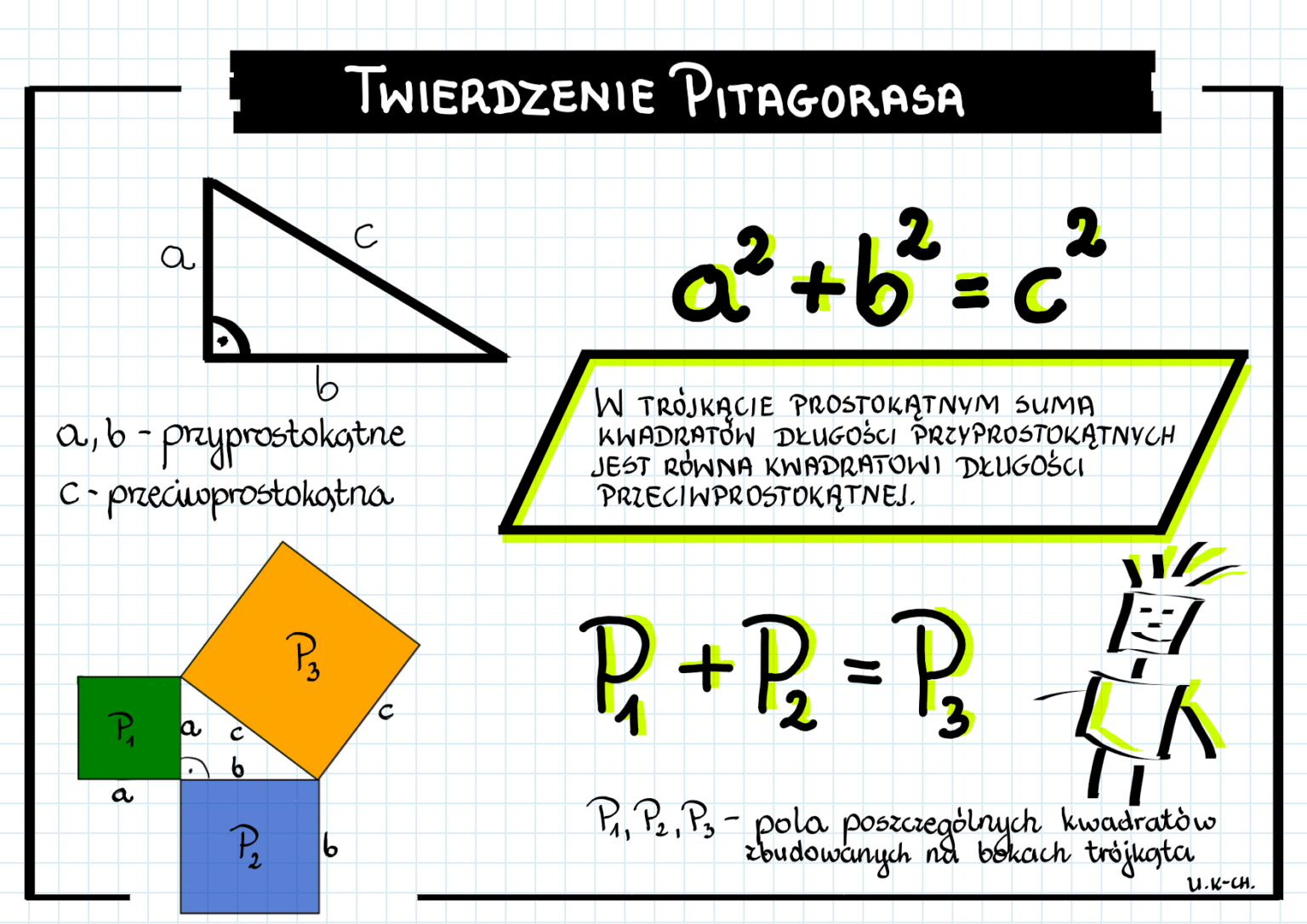
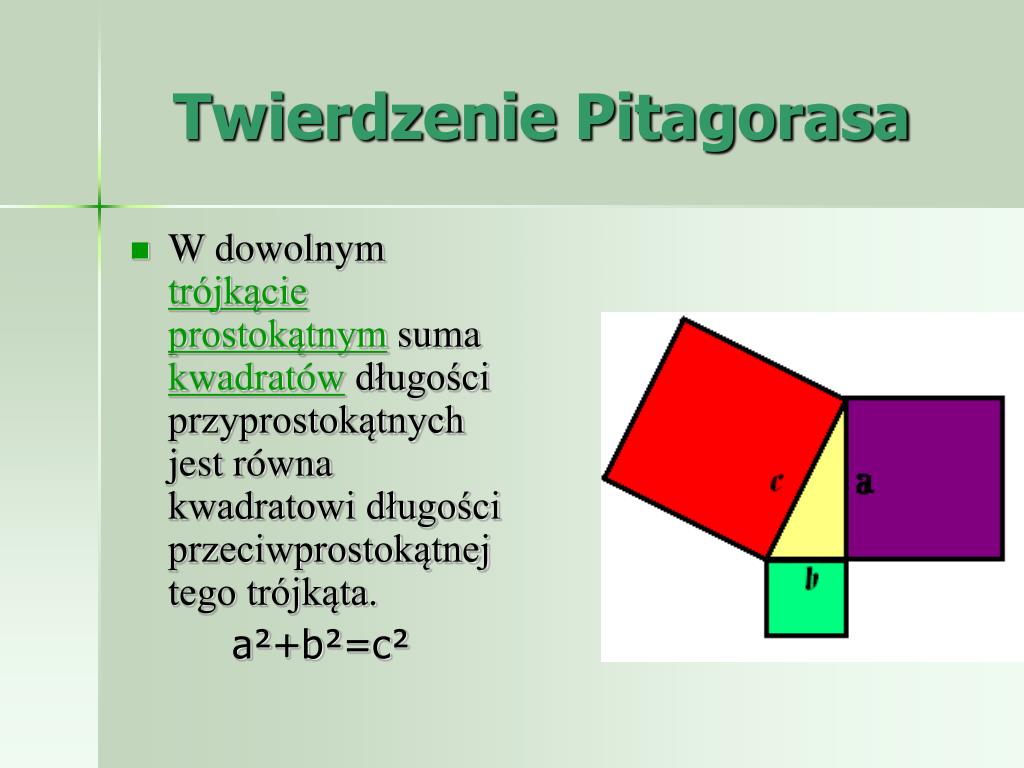
Twierdzenie Pitagorasa to relacja geometryczna, która łączy długości boków trójkąta prostokątnego. Mówi ono, że suma kwadratów długości przyprostokątnych (boków przyległych do kąta prostego) jest równa kwadratowi długości przeciwprostokątnej (boku naprzeciwległego kątowi prostemu). Matematycznie zapisujemy to jako: a² + b² = c², gdzie 'a' i 'b' oznaczają długości przyprostokątnych, a 'c' długość przeciwprostokątnej.

Jak wprowadzić Twierdzenie Pitagorasa w klasie?

Zacznij od przedstawienia trójkąta prostokątnego i zdefiniowania jego elementów: kąta prostego, przyprostokątnych i przeciwprostokątnej. Można to zrobić poprzez:

Wizualizacje: Użyj plansz, prezentacji multimedialnych lub interaktywnych symulacji, które pokazują trójkąt prostokątny i kwadraty zbudowane na jego bokach.
Aktywności praktyczne: Poproś uczniów o narysowanie trójkąta prostokątnego na papierze w kratkę, a następnie o policzenie pól kwadratów zbudowanych na każdym boku. To pozwoli im wizualnie przekonać się o prawdziwości twierdzenia.
Historia: Opowiedz o Pitagorasie i jego wkładzie w rozwój matematyki. Można wspomnieć, że twierdzenie było znane już wcześniej w innych kulturach, ale to właśnie Pitagoras i jego szkoła udowodnili je formalnie.

Zastosowania Twierdzenia Pitagorasa

Po wprowadzeniu samego twierdzenia, kluczowe jest pokazanie uczniom, jak można je wykorzystać w praktyce. Przykłady zastosowań są liczne i dotyczą różnych dziedzin:

Geometria: Obliczanie długości przekątnej kwadratu, prostokąta, rombu. Wyznaczanie wysokości w trójkącie równobocznym lub równoramiennym.
Życie codzienne: Obliczanie długości drabiny potrzebnej do sięgnięcia do określonego punktu na ścianie. Wyznaczanie odległości "na skróty" przez plac, gdy znamy długości boków tworzących kąt prosty. Sprawdzanie, czy szafa zmieści się w przejściu (diagonalnie).
Architektura i budownictwo: Wyznaczanie kątów prostych podczas budowy, obliczanie długości elementów konstrukcyjnych.
Nawigacja: Określanie odległości pomiędzy dwoma punktami na mapie, gdy znamy ich współrzędne.

Przy omawianiu zastosowań, staraj się korzystać z zadań problemowych, które wymagają od uczniów myślenia krytycznego i kreatywnego. Zachęć ich do samodzielnego szukania rozwiązań i prezentowania swoich pomysłów.

Typowe Błędy i Misconcepcje

Podczas nauczania Twierdzenia Pitagorasa, uczniowie często popełniają pewne błędy i mają błędne przekonania. Warto być na nie przygotowanym i aktywnie im przeciwdziałać:

Stosowanie twierdzenia do trójkątów nierównoątnych: Najczęstszy błąd to próba zastosowania twierdzenia do trójkątów, które nie są prostokątne. Podkreślaj, że twierdzenie działa tylko i wyłącznie w trójkątach prostokątnych.
Pomylenie przyprostokątnych z przeciwprostokątną: Upewnij się, że uczniowie dobrze rozumieją definicje tych pojęć i potrafią je rozpoznać w trójkącie.
Błędy w obliczeniach: Pamiętaj o przypominaniu zasad potęgowania i pierwiastkowania, które są niezbędne do rozwiązywania zadań.
Zapominanie o jednostkach: Zwracaj uwagę na jednostki długości i wymagaj od uczniów, aby podawali wyniki z odpowiednimi jednostkami.

Staraj się identyfikować te błędy i reagować na nie indywidualnie. Można to zrobić poprzez regularne sprawdzanie prac domowych, zadawanie pytań podczas lekcji i organizowanie krótkich sprawdzianów.

Angażujące Metody Nauczania

Aby nauka Twierdzenia Pitagorasa była bardziej angażująca, warto zastosować różnorodne metody nauczania:

Gry i zabawy: Wykorzystaj gry planszowe, karciane lub interaktywne, które bazują na twierdzeniu Pitagorasa. Można np. zorganizować konkurs na najszybsze rozwiązywanie zadań.
Projekty: Poproś uczniów o wykonanie projektu, w którym będą musieli zastosować twierdzenie Pitagorasa do rozwiązania realnego problemu. Może to być np. obliczenie długości rampy dla wózków inwalidzkich lub zaprojektowanie domku dla ptaków.
Technologie: Wykorzystaj oprogramowanie geometryczne (np. GeoGebra) do wizualizacji twierdzenia Pitagorasa i eksperymentowania z różnymi trójkątami prostokątnymi.
Zastosowania praktyczne: Zorganizuj wycieczkę terenową, podczas której uczniowie będą mogli zmierzyć długości boków budynków lub drzew i sprawdzić, czy tworzą one trójkąty prostokątne.

Pamiętaj, że kluczem do sukcesu jest urozmaicanie lekcji i dostosowywanie metod nauczania do potrzeb i zainteresowań uczniów. Im bardziej zaangażowani będą uczniowie, tym lepiej zrozumieją i zapamiętają materiał.

Podsumowanie

Twierdzenie Pitagorasa to fundament geometrii, którego zrozumienie jest kluczowe dla dalszej nauki matematyki. Poprzez zastosowanie odpowiednich metod nauczania, uwzględnienie typowych błędów i angażowanie uczniów w proces uczenia się, możemy sprawić, że to pozornie trudne pojęcie stanie się dla nich zrozumiałe i interesujące. Pamiętajmy, że matematyka to nie tylko wzory i definicje, ale przede wszystkim umiejętność logicznego myślenia i rozwiązywania problemów.

Życzę Państwu wielu sukcesów w nauczaniu Twierdzenia Pitagorasa!