Twierdzenie Pitagorasa 2 Gimnazjum Sprawdzian

Znasz ten wzór: a² + b² = c²? To Twierdzenie Pitagorasa! Brzmi groźnie, ale spokojnie, to proste jak bułka z masłem.

Czym jest Twierdzenie Pitagorasa?

Twierdzenie Pitagorasa opisuje relację między bokami w trójkącie prostokątnym. Trójkąt prostokątny to taki trójkąt, który ma jeden kąt prosty (90 stopni). Ten kąt wygląda jak róg kartki.

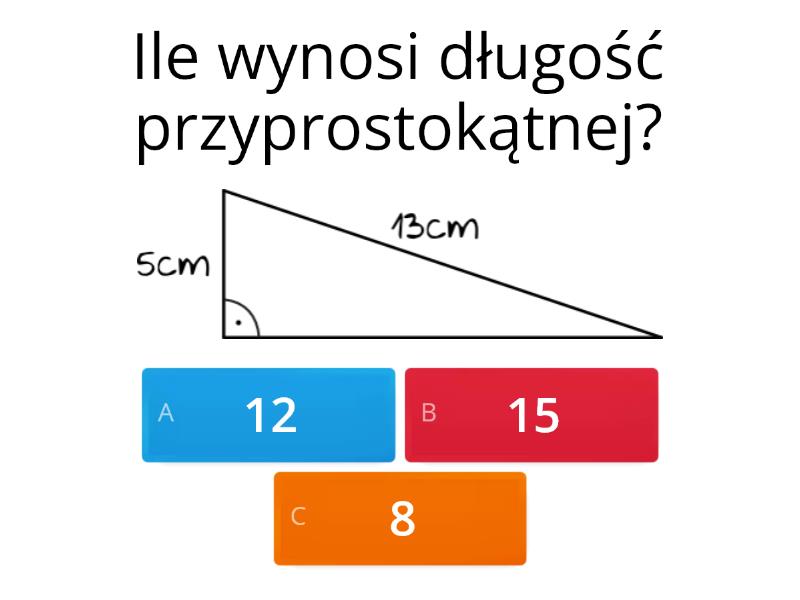
Najdłuższy bok w trójkącie prostokątnym nazywamy przeciwprostokątną. Leży naprzeciwko kąta prostego. Dwa pozostałe boki to przyprostokątne.

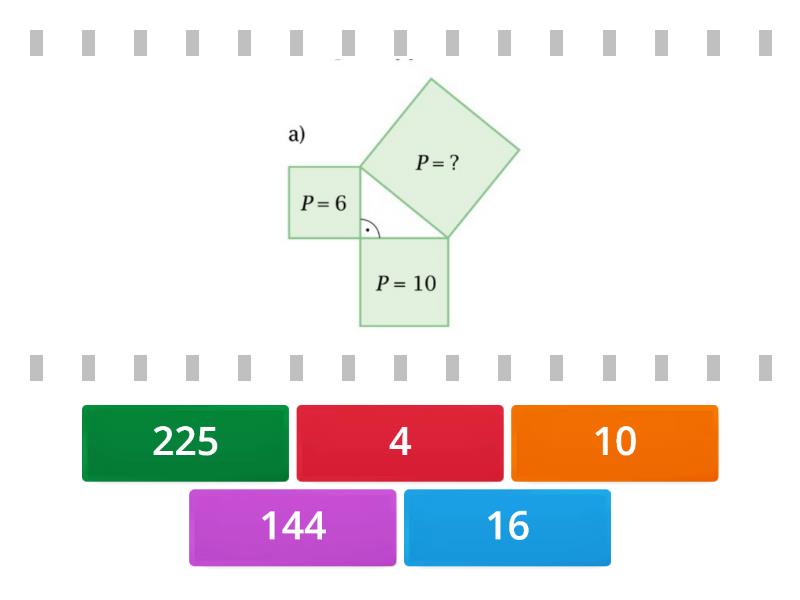
Twierdzenie Pitagorasa mówi, że suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Czyli a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.

Przykłady z życia codziennego

Wyobraź sobie drabinę opartą o ścianę. Ściana i podłoga tworzą kąt prosty. Drabina to przeciwprostokątna, a ściana i odległość od ściany do drabiny to przyprostokątne. Możemy użyć Twierdzenia Pitagorasa, żeby obliczyć długość drabiny, jeśli znamy wysokość ściany i odległość drabiny od ściany.

Inny przykład: chcesz sprawdzić, czy stół jest prostokątny. Mierzysz długości jego boków (a i b) oraz przekątną (c). Jeśli a² + b² = c², to stół ma kąty proste i jest prostokątny!

Jak używać Twierdzenia Pitagorasa?

Załóżmy, że masz trójkąt prostokątny, gdzie jedna przyprostokątna ma długość 3, a druga 4. Chcesz obliczyć długość przeciwprostokątnej. Używasz wzoru: a² + b² = c².

Podstawiasz wartości: 3² + 4² = c². To daje: 9 + 16 = c², czyli 25 = c². Żeby obliczyć c, musisz znaleźć pierwiastek kwadratowy z 25. Pierwiastek kwadratowy z 25 to 5. Czyli długość przeciwprostokątnej wynosi 5.

Sprawdzian z Twierdzenia Pitagorasa

Na sprawdzianie możesz spodziewać się zadań, w których będziesz musiał obliczyć długość jednego z boków trójkąta prostokątnego, znając długości dwóch pozostałych. Mogą też pojawić się zadania, w których trzeba będzie sprawdzić, czy trójkąt jest prostokątny.

Pamiętaj o wzorze a² + b² = c². Zidentyfikuj przyprostokątne i przeciwprostokątną. Podstaw wartości do wzoru i rozwiąż równanie. Powodzenia na sprawdzianie!