Twierdzenie Odwrotne Do Twierdzenia Talesa
W geometrii, twierdzenie Talesa jest fundamentalnym konceptem dotyczącym proporcji i podobieństwa figur. Jednak istnieje równie ważne twierdzenie odwrotne do twierdzenia Talesa, które pozwala nam wnioskować o równoległości prostych na podstawie odpowiednich proporcji. W tym artykule przyjrzymy się bliżej temu twierdzeniu, zrozumiemy jego treść, zastosowania i różnice w porównaniu z twierdzeniem Talesa.
Czym jest Twierdzenie Talesa? Przypomnienie
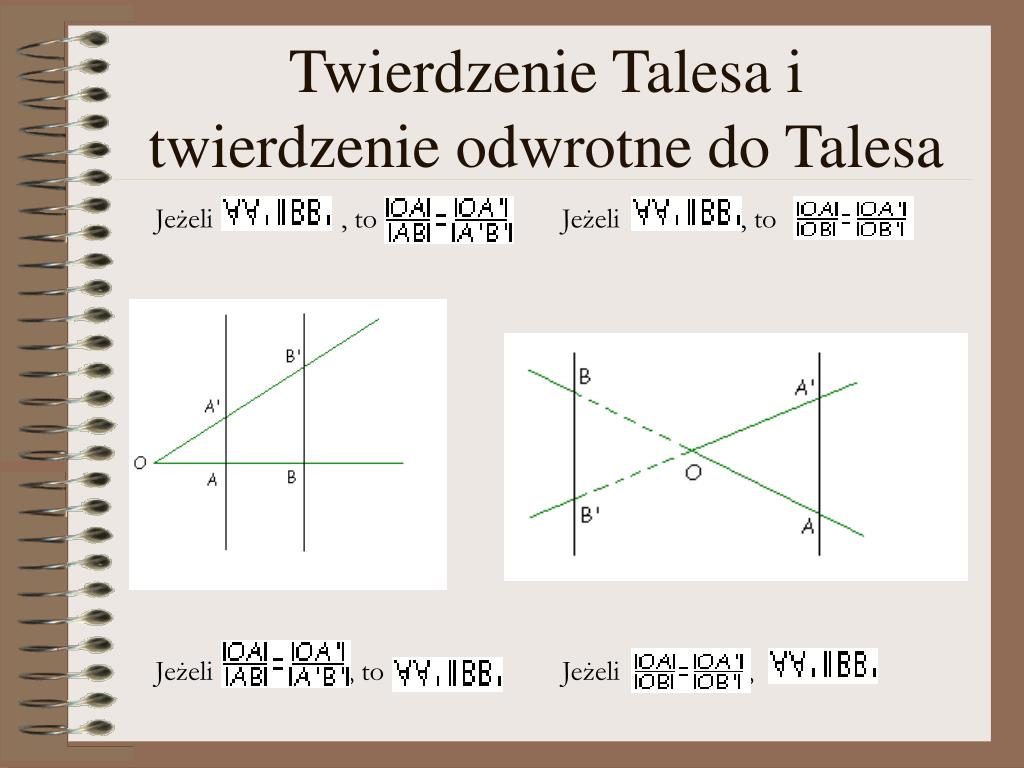
Zanim zagłębimy się w twierdzenie odwrotne, warto przypomnieć sobie klasyczne twierdzenie Talesa. Mówi ono, że:
Jeśli ramiona kąta przetniemy dwiema prostymi równoległymi, to odcinki wyznaczone przez te proste na jednym ramieniu kąta, są proporcjonalne do odpowiednich odcinków wyznaczonych na drugim ramieniu kąta.
Inaczej mówiąc, jeśli mamy kąt o wierzchołku O, a jego ramiona przetniemy prostymi k i l, które są równoległe, to jeśli A i B leżą na jednym ramieniu, a C i D leżą na drugim ramieniu, to zachodzi proporcja:
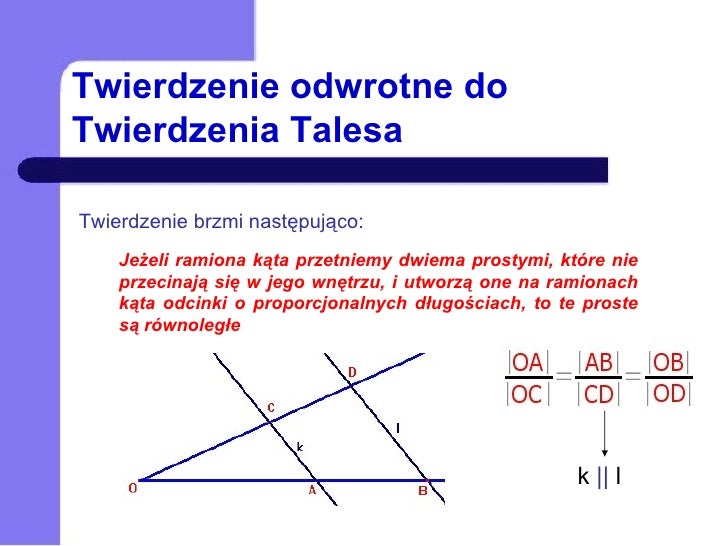
OA/AB = OC/CD
Twierdzenie Talesa pozwala nam, znając równoległość prostych, wnioskować o proporcjonalności odpowiednich odcinków.
Twierdzenie Odwrotne do Twierdzenia Talesa: Sedno
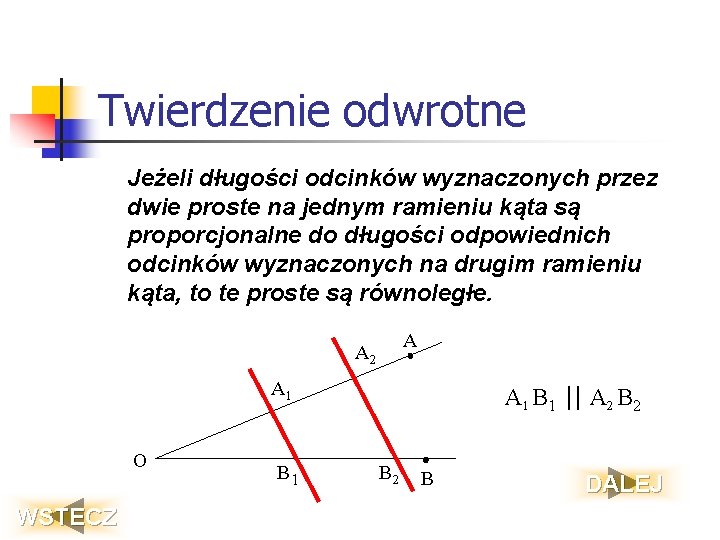
Twierdzenie Odwrotne do Twierdzenia Talesa robi dokładnie odwrotnie. Umożliwia nam wnioskowanie o równoległości prostych, jeśli wiemy, że odpowiednie odcinki są proporcjonalne. Brzmi ono następująco:
Jeśli ramiona kąta przetniemy dwiema prostymi, a odcinki wyznaczone przez te proste na jednym ramieniu kąta są proporcjonalne do odpowiednich odcinków wyznaczonych na drugim ramieniu kąta, to te proste są równoległe.
Używając tych samych oznaczeń co wcześniej, jeśli mamy kąt o wierzchołku O, a jego ramiona przecinają proste k i l w punktach A, B i C, D odpowiednio, oraz zachodzi proporcja OA/AB = OC/CD, to możemy stwierdzić, że proste k i l są równoległe.
Kluczowe jest tutaj, aby proporcja była spełniona. Jeśli proporcja nie zachodzi, to proste *nie* są równoległe.
Przykład Ilustrujący Twierdzenie Odwrotne
Załóżmy, że mamy kąt o wierzchołku O. Na jednym ramieniu kąta znajdują się punkty A i B, a na drugim punkty C i D. Wiemy, że:
- OA = 3 cm
- AB = 6 cm
- OC = 4 cm
- CD = 8 cm
Sprawdźmy, czy zachodzi proporcja:
OA/AB = 3/6 = 1/2
OC/CD = 4/8 = 1/2
Ponieważ OA/AB = OC/CD, możemy wnioskować, że proste przechodzące przez punkty A, C oraz B, D są równoległe na mocy Twierdzenia Odwrotnego do Twierdzenia Talesa.
Zastosowania Twierdzenia Odwrotnego
Twierdzenie odwrotne do twierdzenia Talesa znajduje zastosowanie w różnych problemach geometrycznych, w tym:
- Konstrukcje Geometryczne: Umożliwia konstruowanie prostych równoległych za pomocą cyrkla i linijki, wykorzystując proporcje odcinków.
- Sprawdzanie Równoległości: Pomaga w weryfikacji, czy dane proste są równoległe, bez konieczności bezpośredniego mierzenia kątów między nimi.
- Podobieństwo Figur: Jest użyteczne w dowodzeniu podobieństwa figur, gdzie równoległość prostych odgrywa istotną rolę.
- Rozwiązywanie Zadań: Ułatwia rozwiązywanie zadań geometrycznych, w których trzeba wykazać równoległość prostych.
Różnica między Twierdzeniem Talesa a Twierdzeniem Odwrotnym
Najważniejsza różnica polega na tym, co jest dane, a co jest wnioskowane:
- Twierdzenie Talesa: Dane są proste równoległe, a wnioskujemy o proporcjonalności odcinków.
- Twierdzenie Odwrotne do Twierdzenia Talesa: Dana jest proporcjonalność odcinków, a wnioskujemy o równoległości prostych.
Pamiętanie o tej różnicy jest kluczowe do poprawnego stosowania obu twierdzeń w zadaniach geometrycznych.
Podsumowanie
Twierdzenie Odwrotne do Twierdzenia Talesa jest potężnym narzędziem w geometrii, pozwalającym na wnioskowanie o równoległości prostych na podstawie proporcji odcinków. Jego zrozumienie i poprawne stosowanie pozwala rozwiązywać szereg problemów geometrycznych, a także lepiej zrozumieć zależności między równoległością a proporcjonalnością. Pamiętajmy, że kluczem do sukcesu jest poprawne rozpoznanie, kiedy i jak zastosować to twierdzenie, rozróżniając je od bezpośredniego twierdzenia Talesa.