Twierdzenie O Odcinku łączącym środki Boków W Trójkącie

Okej, dobrze rozumiem. Oto artykuł wyjaśniający twierdzenie o odcinku łączącym środki boków w trójkącie, napisany w języku polskim, w prosty sposób, bez zbędnych wstępów i dowodów, oraz z zachowaniem podanych zasad.

Wyobraź sobie trójkąt. Jakikolwiek trójkąt. Może być równoboczny, równoramienny, prostokątny, ostrokątny, rozwartokątny… naprawdę, nie ma znaczenia. To twierdzenie działa dla wszystkich trójkątów.

Teraz znajdźmy środki dwóch boków tego trójkąta. Pamiętaj, środek boku to punkt, który dzieli bok na dwie równe części. Zaznacz te środki. Mamy dwa punkty – jeden na jednym boku i drugi na drugim boku trójkąta.

Połącz te dwa punkty linią prostą. Ta linia, ten odcinek, który właśnie narysowałeś, jest tym, o którym mówi nasze twierdzenie. Nazywamy go odcinkiem łączącym środki boków.

Co to twierdzenie mówi o tym odcinku? Mówi dwie bardzo ważne rzeczy.

Odcinek łączący środki boków trójkąta jest równoległy do trzeciego boku tego trójkąta.
Odcinek łączący środki boków trójkąta jest równy połowie długości trzeciego boku tego trójkąta.

Proste, prawda? Spójrzmy na to jeszcze raz, krok po kroku, żeby to dobrze zrozumieć.

Jak to Działa?

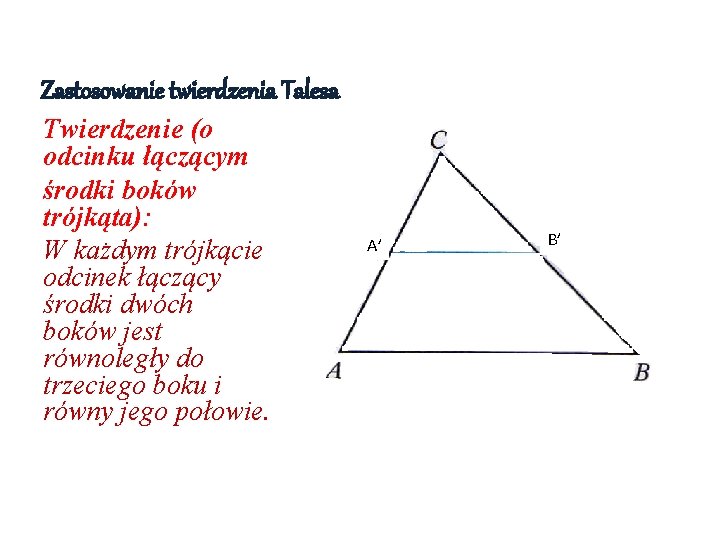
Mamy trójkąt. Oznaczmy jego wierzchołki literami A, B i C. Czyli mamy trójkąt ABC. Znajdźmy środek boku AB. Oznaczmy go literą D. Znajdźmy środek boku AC. Oznaczmy go literą E.

Teraz narysujmy odcinek DE. Ten odcinek DE to nasz odcinek łączący środki boków.

Twierdzenie mówi nam, że odcinek DE jest równoległy do boku BC. Co to znaczy równoległy? To znaczy, że niezależnie jak bardzo byśmy przedłużali te dwa odcinki (DE i BC), nigdy się nie przetną. Są jak dwie proste tory kolejowe – biegną obok siebie, w tym samym kierunku, ale nigdy się nie spotykają.

Dodatkowo, twierdzenie mówi, że długość odcinka DE jest dokładnie połową długości boku BC. Czyli, jeśli bok BC ma długość 10 cm, to odcinek DE ma długość 5 cm. Jeśli bok BC ma długość 2 metry, to odcinek DE ma długość 1 metra. Zawsze połowa!

To jest całe twierdzenie. Wydaje się bardzo proste, a w praktyce okazuje się bardzo przydatne przy rozwiązywaniu zadań z geometrii.

Przykłady i Zastosowania

Żeby lepiej to zrozumieć, spójrzmy na kilka przykładów.

Załóżmy, że mamy trójkąt, a długość jednego z jego boków wynosi 12 cm. Odcinek łączący środki pozostałych dwóch boków tego trójkąta ma długość? Zgodnie z twierdzeniem, połowę długości tego boku, czyli 6 cm.

A co jeśli wiemy, że odcinek łączący środki boków trójkąta ma długość 4 cm? Jaka jest długość boku, do którego ten odcinek jest równoległy? Skoro odcinek łączący środki boków jest połową długości tego boku, to bok ten musi mieć długość dwa razy większą, czyli 8 cm.

Twierdzenie to jest używane w wielu zadaniach, na przykład do obliczania długości odcinków, udowadniania równoległości prostych, czy też do rozwiązywania bardziej złożonych problemów geometrycznych. Często pojawia się w zadaniach dotyczących podobieństwa trójkątów i pól figur.

Wyobraź sobie na przykład, że masz trójkąt ABC, a wewnątrz niego narysowano odcinek DE, łączący środki boków AB i AC. Teraz, jeśli narysujesz odcinek EF łączący środek boku AC (czyli punkt E) ze środkiem boku BC (oznaczmy go literą F), to otrzymasz kolejny odcinek łączący środki boków. I znowu, odcinek EF będzie równoległy do boku AB i będzie miał długość równą połowie długości AB.

Możesz kontynuować ten proces, znajdując środek boku BC (czyli punkt F) i łącząc go ze środkiem boku AB (czyli punkt D). Otrzymasz odcinek FD, który będzie równoległy do boku AC i będzie miał długość równą połowie długości AC.

Co ciekawe, tworząc te odcinki łączące środki boków, dzielisz oryginalny trójkąt ABC na cztery mniejsze trójkąty. Wszystkie te cztery trójkąty są podobne do trójkąta ABC, a ich pola są cztery razy mniejsze niż pole trójkąta ABC. To wynika bezpośrednio z twierdzenia o odcinku łączącym środki boków.

Podsumowując, twierdzenie o odcinku łączącym środki boków jest potężnym narzędziem, które upraszcza wiele problemów geometrycznych. Zapamiętaj dwie kluczowe rzeczy: równoległość i połowa długości. Te dwa fakty otwierają drzwi do rozwiązywania różnorodnych zadań. Pamiętaj, że odcinek ten łączy środki dwóch boków i jest równoległy do trzeciego.

Mam nadzieję, że teraz rozumiesz to twierdzenie o wiele lepiej. Powodzenia w rozwiązywaniu zadań!