Trójkaty Szczególne 30 60 90

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre trójkąty wydają się "łatwiejsze" do obliczenia niż inne? Często to zasługa ich specjalnych właściwości. Jeśli miałeś kiedykolwiek problem z trygonometrią i obliczaniem długości boków trójkąta, ten artykuł jest dla Ciebie. Skupimy się na jednym z najbardziej przydatnych narzędzi w geometrii: trójkącie szczególnym 30-60-90.

Wyobraź sobie sytuację: pracujesz nad projektem budowlanym i potrzebujesz szybko wyznaczyć długość krokwy dachu. Nie masz czasu na żmudne obliczenia trygonometryczne. Co robisz? Jeśli znasz właściwości trójkąta 30-60-90, zadanie staje się dziecinnie proste! Ten trójkąt, to swoisty "shortcut" do rozwiązywania wielu problemów.

Co to jest trójkąt szczególny 30-60-90?

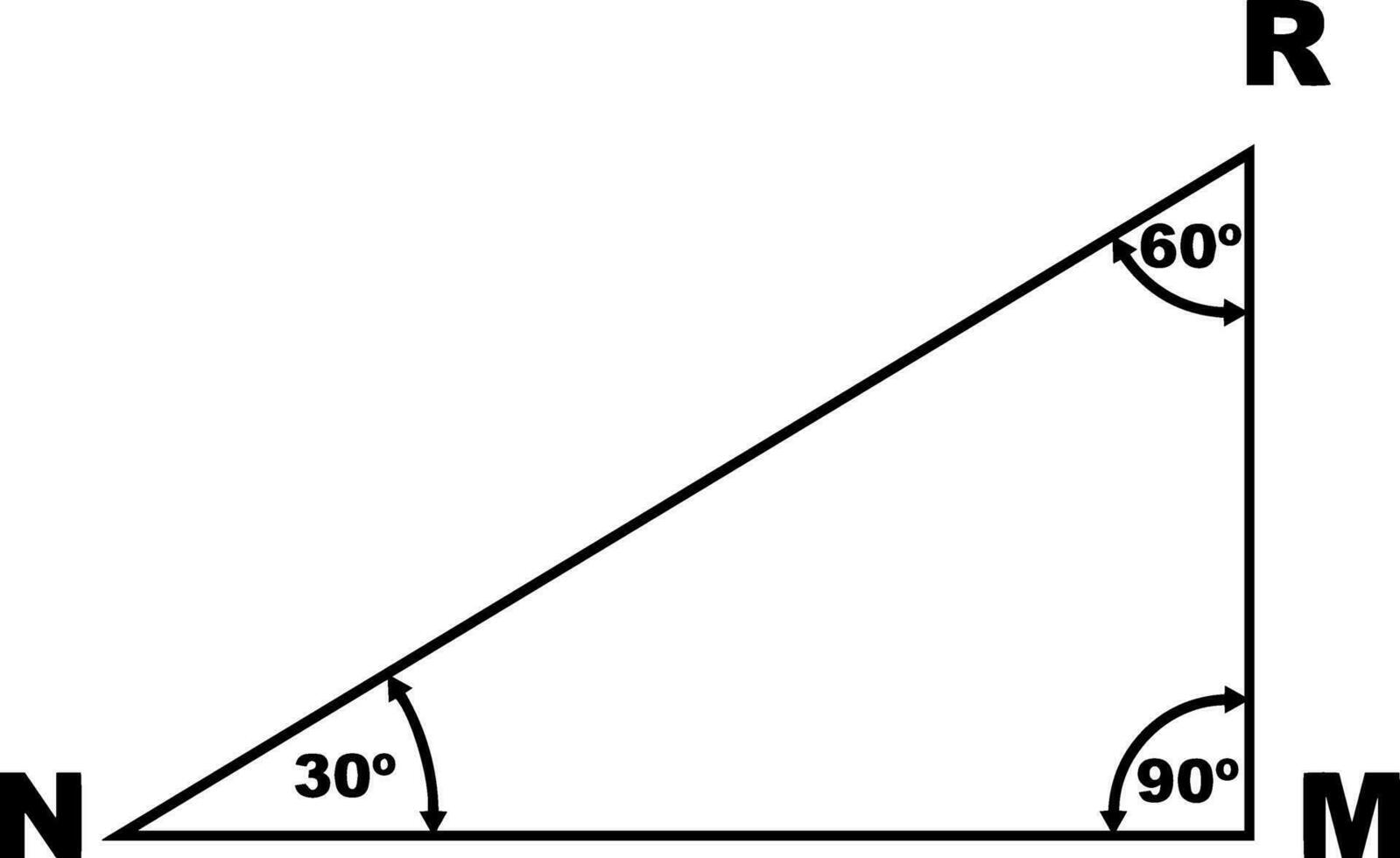
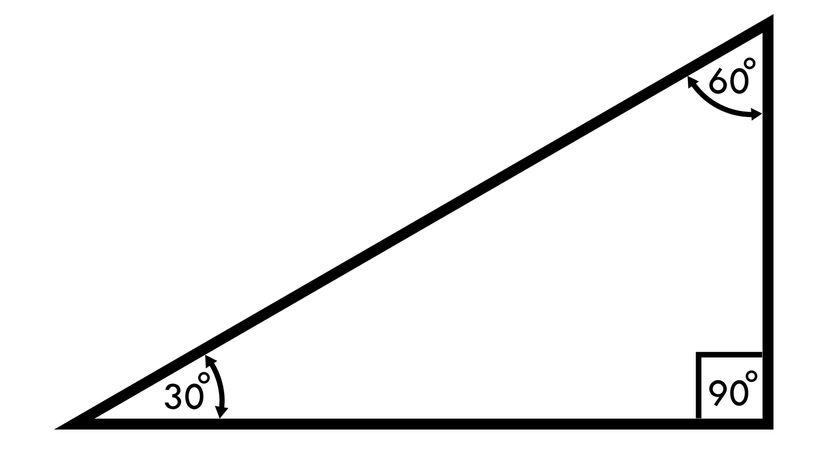
Trójkąt 30-60-90 to trójkąt prostokątny, którego kąty wewnętrzne mają miary 30°, 60° i 90°. Jego niezwykłość polega na tym, że długości jego boków pozostają w stałej proporcji. To fundamentalna wiedza, która ułatwia rozwiązywanie wielu problemów geometrycznych i trygonometrycznych.

Proporcje boków: Klucz do sukcesu

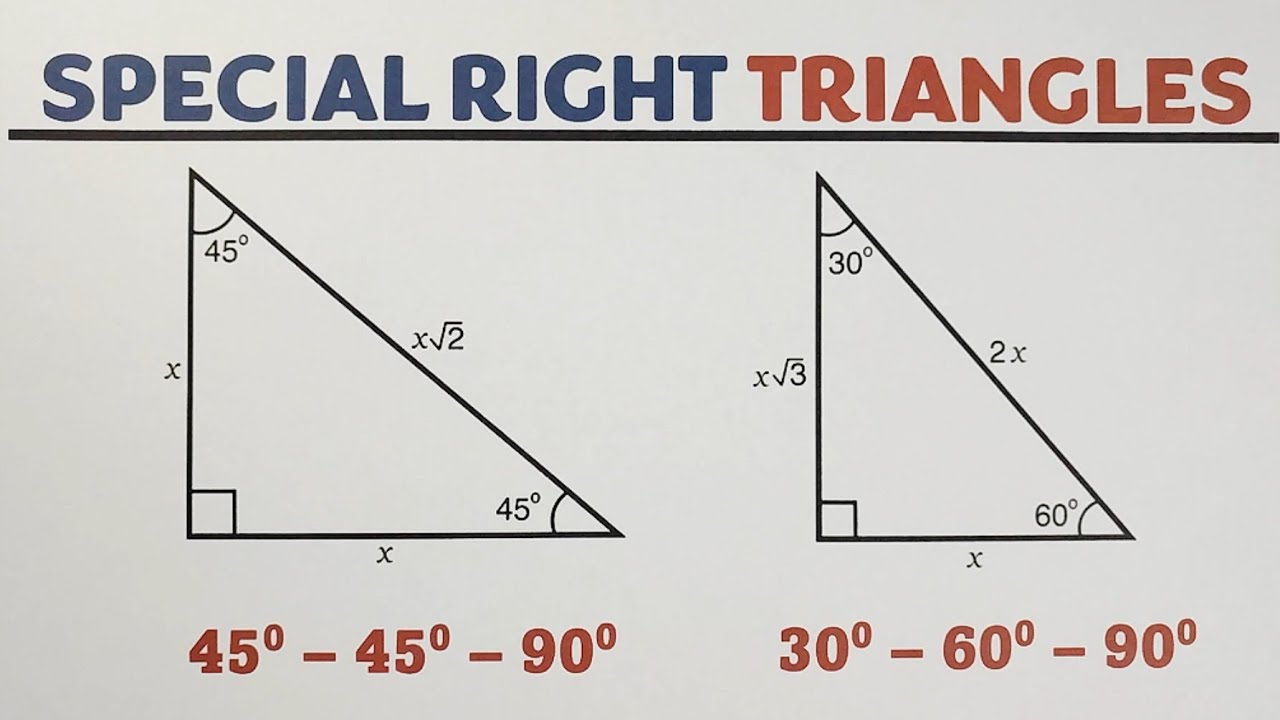
Najważniejszą rzeczą do zapamiętania jest stosunek długości boków w trójkącie 30-60-90. Jeśli krótszą przyprostokątną (leżącą naprzeciwko kąta 30°) oznaczymy jako a, to:

Dłuższa przyprostokątna (leżąca naprzeciwko kąta 60°) będzie miała długość a√3.
Przeciwprostokątna (leżąca naprzeciwko kąta 90°) będzie miała długość 2a.

Zapamiętaj ten stosunek: a : a√3 : 2a. To jest klucz do szybkiego rozwiązywania zadań!

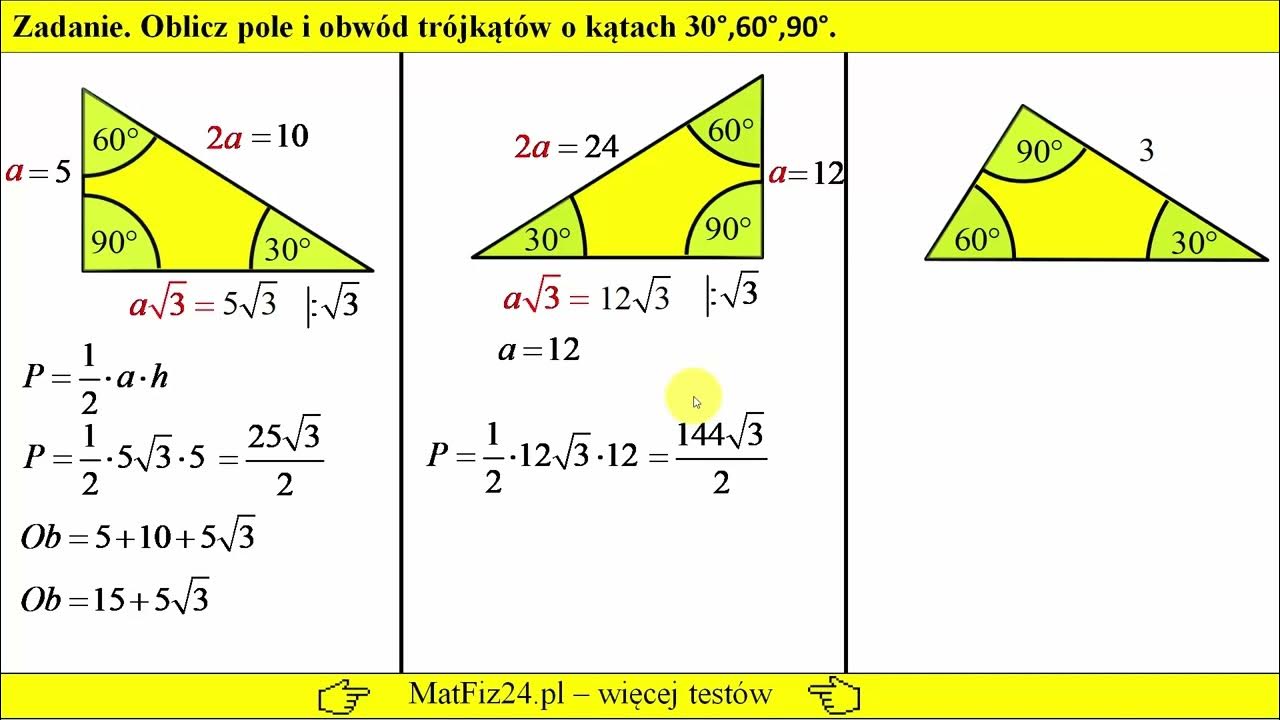
Przykład: Załóżmy, że krótsza przyprostokątna w trójkącie 30-60-90 ma długość 5 cm. W takim razie:

Dłuższa przyprostokątna ma długość 5√3 cm.
Przeciwprostokątna ma długość 10 cm.

Jak widzisz, znając tylko długość jednej strony, możemy błyskawicznie obliczyć długości pozostałych boków. To ogromne ułatwienie!

Skąd się bierze ta proporcja?

Zastanawiasz się pewnie, dlaczego akurat taki stosunek długości boków? Wywodzi się on z trójkąta równobocznego. Wyobraź sobie trójkąt równoboczny o boku długości 2a. Jeśli przetniemy go na pół wzdłuż wysokości, otrzymamy dwa identyczne trójkąty prostokątne o kątach 30°, 60° i 90°.

Przeciwprostokątna (czyli bok wyjściowego trójkąta równobocznego) ma długość 2a. Krótsza przyprostokątna to połowa boku trójkąta równobocznego, czyli a. Długość dłuższej przyprostokątnej (wysokość trójkąta równobocznego) możemy obliczyć z twierdzenia Pitagorasa: a² + b² = (2a)², co prowadzi do b = a√3.

W ten sposób dowiedliśmy, skąd bierze się magiczny stosunek a : a√3 : 2a!

Zastosowania w praktyce

Trójkąt 30-60-90 znajduje zastosowanie w wielu dziedzinach, nie tylko w matematyce.

Architektura i budownictwo: Obliczanie długości krokwi dachowych, wyznaczanie kątów nachylenia.
Inżynieria: Projektowanie konstrukcji, obliczanie sił działających na elementy.
Nawigacja: Określanie odległości i kierunków.
Gry komputerowe i grafika 3D: Tworzenie realistycznych scen i animacji.
Trygonometria: Rozwiązywanie równań trygonometrycznych, obliczanie wartości funkcji trygonometrycznych dla kątów 30° i 60°.

Pomyśl, jak często w życiu codziennym spotykasz się z trójkątami – od dachu domu, przez kształt kawałka pizzy, po konstrukcję mostu. Znajomość trójkąta 30-60-90 pozwala na szybkie i efektywne rozwiązywanie wielu problemów!

Jak efektywnie uczyć się i zapamiętać właściwości trójkąta 30-60-90?

Samo przeczytanie o trójkącie 30-60-90 to za mało. Kluczem do sukcesu jest praktyka i powtarzanie. Oto kilka sprawdzonych metod:

Rozwiązywanie zadań: Im więcej zadań rozwiążesz, tym lepiej utrwalisz wiedzę. Zacznij od prostych przykładów i stopniowo przechodź do bardziej skomplikowanych.
Tworzenie własnych przykładów: Samodzielne wymyślanie zadań zmusza do głębszego zrozumienia tematu.
Wykorzystanie wizualizacji: Rysuj trójkąty 30-60-90 i oznaczaj długości ich boków. Możesz użyć kolorów, aby lepiej zapamiętać proporcje.
Uczenie kogoś innego: Najlepszym sposobem na utrwalenie wiedzy jest przekazanie jej komuś innemu. Wytłumacz znajomemu, jak działa trójkąt 30-60-90.
Korzystanie z aplikacji i stron internetowych: Istnieje wiele darmowych narzędzi online, które pomogą Ci w nauce geometrii i trygonometrii.
Skojarzenia: Stwórz skojarzenia, które pomogą Ci zapamiętać proporcje. Na przykład, pomyśl o √3 jako o "dłuższej" liczbie, więc przypisz ją do dłuższej przyprostokątnej.

Pamiętaj: Regularność jest kluczowa. Nawet krótkie, ale systematyczne sesje nauki przyniosą lepsze efekty niż sporadyczne, długie maratony.

Częste błędy i jak ich unikać

Nawet osoby dobrze znające teorię mogą popełniać błędy w praktyce. Oto kilka typowych pułapek:

Pomylenie kątów: Upewnij się, że poprawnie identyfikujesz kąty 30° i 60°. To kluczowe do prawidłowego przypisania długości boków.
Błędne podstawianie: Sprawdź, czy podstawiasz prawidłowe wartości do wzorów. Pomyłka w jednej liczbie może zrujnować całe rozwiązanie.
Zapominanie o jednostkach: Pamiętaj o podawaniu jednostek długości (cm, m, km itp.).
Próba zastosowania do innych trójkątów: Właściwości trójkąta 30-60-90 dotyczą wyłącznie trójkątów o tych kątach. Nie próbuj stosować ich do innych trójkątów prostokątnych.

Wskazówka: Zawsze rysuj schemat trójkąta i oznaczaj wszystkie znane dane. To pomoże Ci uniknąć pomyłek.

Podsumowanie

Trójkąt szczególny 30-60-90 to niezwykle potężne narzędzie, które znacznie ułatwia rozwiązywanie problemów geometrycznych i trygonometrycznych. Znajomość proporcji jego boków pozwala na szybkie obliczanie długości nieznanych boków, co jest przydatne w wielu dziedzinach życia.

Nie zrażaj się, jeśli na początku wydaje Ci się to trudne. Kluczem do sukcesu jest praktyka, powtarzanie i systematyczność. Wykorzystaj wskazówki zawarte w tym artykule, rozwiązuj zadania, wizualizuj i ucz się na błędach. Z czasem trójkąt 30-60-90 stanie się Twoim wiernym sprzymierzeńcem w świecie matematyki!

Więc następnym razem, gdy zobaczysz trójkąt 30-60-90, nie uciekaj! Podejdź do niego z uśmiechem i wykorzystaj swoją wiedzę, aby błyskawicznie rozwiązać problem. Powodzenia!