Trojkaty Prostokatne Abc I Def

Rozważmy sytuację, w której musisz obliczyć długość dachu spadzistego, zmierzyć wysokość masztu, który jest niedostępny, albo upewnić się, że róg nowo wybudowanej ściany jest idealnie prosty. Brzmi znajomo? W wielu dziedzinach życia, od budownictwa po nawigację, spotykamy się z sytuacjami, w których geometria odgrywa kluczową rolę. A jednym z fundamentalnych elementów geometrii jest trójkąt prostokątny. W tym artykule przyjrzymy się dwóm konkretnym trójkątom prostokątnym: ABC i DEF, analizując ich właściwości, zastosowania i powiązania.

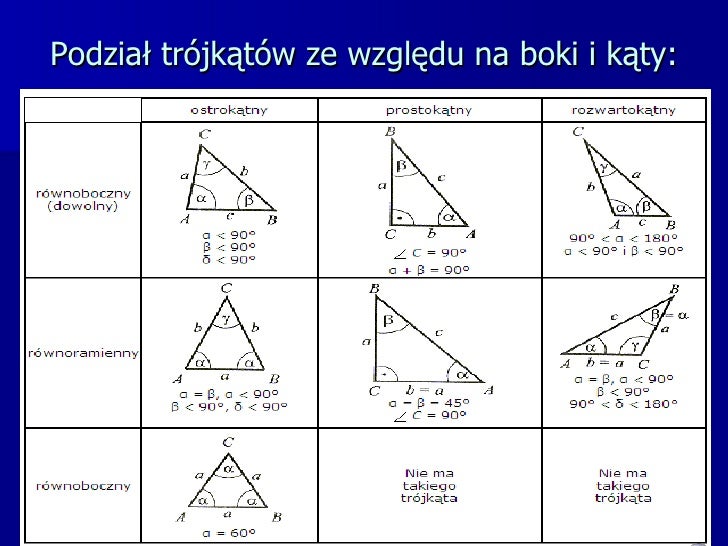
Podstawy Trójkąta Prostokątnego

Zanim przejdziemy do szczegółów dotyczących trójkątów ABC i DEF, przypomnijmy sobie podstawowe cechy trójkąta prostokątnego:

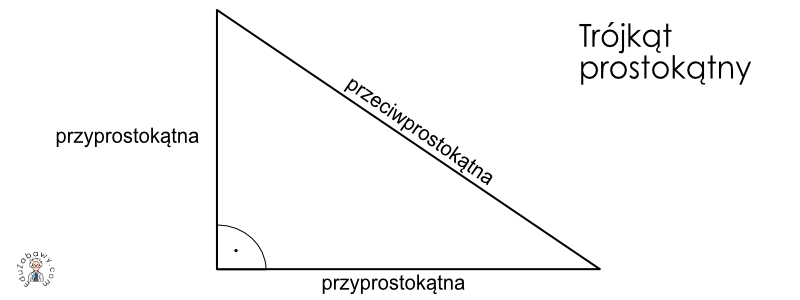
• Kąt prosty: Posiada jeden kąt o mierze 90 stopni.
• Przeciwprostokątna: Najdłuższy bok, leżący naprzeciwko kąta prostego.
• Przyprostokątne: Dwa pozostałe boki, które tworzą kąt prosty.
• Twierdzenie Pitagorasa: Podstawowa zależność: a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.

Twierdzenie Pitagorasa jest absolutnym fundamentem w rozwiązywaniu problemów związanych z trójkątami prostokątnymi. Pozwala ono obliczyć długość jednego z boków, jeśli znamy długości dwóch pozostałych.

Trójkąt Prostokątny ABC

Załóżmy, że mamy trójkąt prostokątny ABC, gdzie kąt przy wierzchołku B jest kątem prostym (∠ABC = 90°). Oznacza to, że bok AC jest przeciwprostokątną, a boki AB i BC są przyprostokątnymi. Spróbujmy przeanalizować kilka scenariuszy:

Scenariusz 1: Znane długości przyprostokątnych

Powiedzmy, że AB = 3 cm i BC = 4 cm. Jak obliczyć długość przeciwprostokątnej AC?

Korzystamy z twierdzenia Pitagorasa: AC² = AB² + BC² = 3² + 4² = 9 + 16 = 25. Zatem AC = √25 = 5 cm. Ten konkretny trójkąt (3-4-5) jest klasycznym przykładem trójkąta pitagorejskiego – trójkąta, w którym wszystkie boki mają długości wyrażone liczbami całkowitymi.

Scenariusz 2: Znana długość przeciwprostokątnej i jednej przyprostokątnej

Załóżmy, że AC = 13 cm i AB = 5 cm. Jak obliczyć długość przyprostokątnej BC?

Ponownie używamy twierdzenia Pitagorasa, ale tym razem przekształcamy wzór: BC² = AC² - AB² = 13² - 5² = 169 - 25 = 144. Zatem BC = √144 = 12 cm. Kolejny trójkąt pitagorejski (5-12-13).

Kąty w trójkącie ABC

Oprócz długości boków, możemy również obliczyć miary kątów w trójkącie ABC, korzystając z funkcji trygonometrycznych (sinus, cosinus, tangens). Na przykład:

• sin(∠BAC) = BC/AC
• cos(∠BAC) = AB/AC
• tan(∠BAC) = BC/AB

Znając stosunek długości boków, możemy użyć funkcji arcus (arcsin, arccos, arctan) na kalkulatorze, aby obliczyć miarę kąta w stopniach lub radianach.

Trójkąt Prostokątny DEF

Przejdźmy teraz do drugiego trójkąta prostokątnego, DEF, gdzie kąt przy wierzchołku E jest kątem prostym (∠DEF = 90°). Bok DF jest przeciwprostokątną, a DE i EF są przyprostokątnymi.

Scenariusz 1: Podobieństwo trójkątów

Załóżmy, że trójkąt DEF jest podobny do trójkąta ABC. Co to oznacza? Oznacza to, że kąty w trójkącie DEF są równe odpowiednim kątom w trójkącie ABC, a długości boków są proporcjonalne. Powiedzmy, że trójkąt DEF jest powiększeniem trójkąta ABC w skali 2. To znaczy, DF = 2 * AC, DE = 2 * AB, i EF = 2 * BC.

Jeśli AB = 3 cm, BC = 4 cm, i AC = 5 cm (jak w naszym poprzednim przykładzie trójkąta ABC), to DE = 6 cm, EF = 8 cm, i DF = 10 cm.

Scenariusz 2: Nieznane boki

Załóżmy, że DE = 7 cm i DF = 25 cm. Jak obliczyć długość boku EF?

Korzystamy z twierdzenia Pitagorasa: EF² = DF² - DE² = 25² - 7² = 625 - 49 = 576. Zatem EF = √576 = 24 cm.

Zastosowania praktyczne

Trójkąty prostokątne, takie jak ABC i DEF, znajdują zastosowanie w wielu dziedzinach, między innymi:

• Budownictwo: Wyznaczanie kątów prostych, obliczanie długości krokwi dachowych.
• Nawigacja: Określanie pozycji na mapie, obliczanie odległości.
• Inżynieria: Projektowanie mostów, budynków i innych konstrukcji.
• Fizyka: Rozkładanie sił na składowe.
• Grafika komputerowa: Obliczenia związane z perspektywą i oświetleniem.

Porównanie Trójkątów ABC i DEF

Chociaż oba trójkąty, ABC i DEF, są trójkątami prostokątnymi, mogą się różnić pod wieloma względami:

• Długości boków: Mogą mieć różne długości boków.
• Miary kątów: Chociaż jeden kąt jest zawsze prosty, pozostałe dwa kąty mogą mieć różne miary, chyba że są trójkątami podobnymi.
• Położenie w przestrzeni: Mogą być zorientowane w różny sposób.

Kluczowe jest zrozumienie, że choć oba trójkąty spełniają definicję trójkąta prostokątnego, mogą posiadać unikalne właściwości i być wykorzystywane w różnych kontekstach.

Adresowanie Kontrargumentów

Niektórzy mogą argumentować, że skupianie się na trójkątach prostokątnych jest zbyt wąskie, a geometria to znacznie szerszy temat. To prawda, geometria obejmuje wiele różnych kształtów i figur. Jednak trójkąt prostokątny jest elementem fundamentalnym, na którym opierają się liczne inne koncepcje geometryczne. Znajomość jego właściwości jest niezbędna do zrozumienia bardziej złożonych zagadnień.

Inny argument może dotyczyć dostępności oprogramowania komputerowego, które automatycznie rozwiązuje problemy geometryczne. Chociaż oprogramowanie to jest bardzo przydatne, rozumienie podstawowych zasad geometrii pozwala na efektywne korzystanie z tych narzędzi i weryfikację poprawności wyników. "Black box" bez zrozumienia, to droga do błędów.

Klucz do sukcesu: Praktyka

Najlepszym sposobem na zrozumienie i zapamiętanie właściwości trójkątów prostokątnych jest ćwiczenie. Rozwiązuj różne zadania, obliczaj długości boków, miary kątów, a także staraj się wizualizować te trójkąty w różnych kontekstach. Im więcej ćwiczysz, tym bardziej naturalne staną się dla Ciebie te koncepcje.

Podsumowanie

Trójkąty prostokątne ABC i DEF, choć wydają się być prostymi figurami geometrycznymi, są niezwykle potężnym narzędziem w wielu dziedzinach. Zrozumienie ich właściwości, zwłaszcza twierdzenia Pitagorasa, otwiera drzwi do rozwiązywania problemów praktycznych i teoretycznych. Pamiętaj, że kluczem do sukcesu jest praktyka i ciągłe poszerzanie swojej wiedzy.

Czy zastanawiałeś się kiedyś, jak często w ciągu jednego dnia korzystasz z zasad geometrii, nawet o tym nie wiedząc?