Trojkaty I Czworokaty 8 Klasa

Zastanawiasz się nad geometrią, a konkretnie nad trójkątami i czworokątami? Dobra wiadomość! Ten artykuł jest właśnie dla Ciebie. Skierowany do uczniów ósmej klasy (ale i dla każdego, kto chce sobie odświeżyć wiedzę!), pomoże Ci zrozumieć podstawowe pojęcia i wzory dotyczące tych ważnych figur geometrycznych. Przygotuj się na przygodę w fascynującym świecie kątów, boków i powierzchni!

Trójkąty – Fundament Geometrii

Trójkąt, jak sama nazwa wskazuje, to figura geometryczna, która ma trzy boki i trzy kąty. Ale to dopiero początek! Istnieje wiele różnych rodzajów trójkątów, a każdy z nich ma swoje unikalne właściwości.

Rodzaje Trójkątów

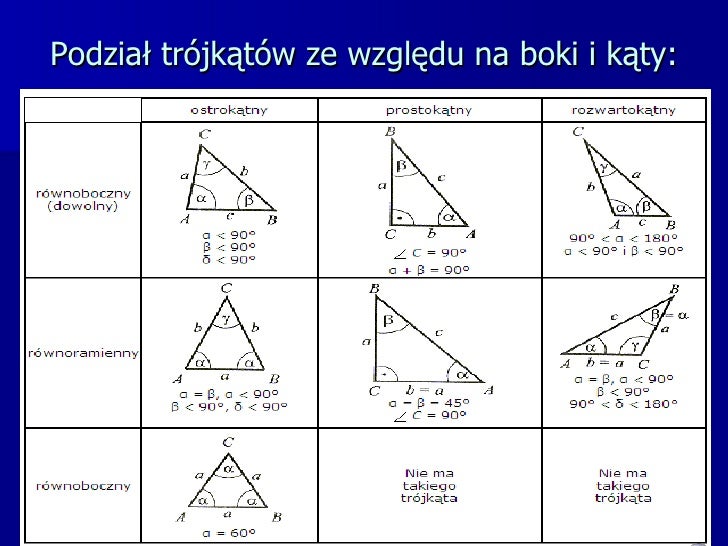
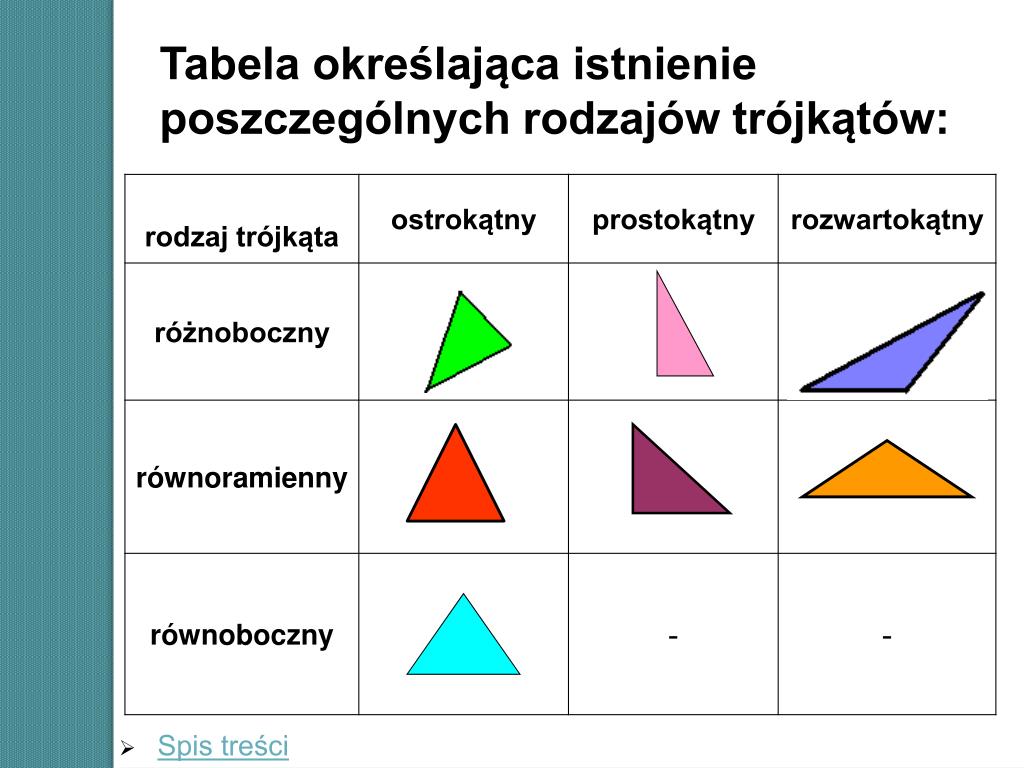
Trójkąty możemy klasyfikować na podstawie długości ich boków lub miar ich kątów. Przyjrzyjmy się bliżej:

Trójkąt Równoboczny: Posiada wszystkie trzy boki równe i wszystkie trzy kąty równe (po 60 stopni). Jest to najbardziej "regularny" typ trójkąta.
Trójkąt Równoramienny: Posiada dwa boki równe (ramiona) i dwa kąty równe (kąty przy podstawie).
Trójkąt Różnoboczny: Posiada wszystkie trzy boki różnej długości i wszystkie trzy kąty różnej miary.
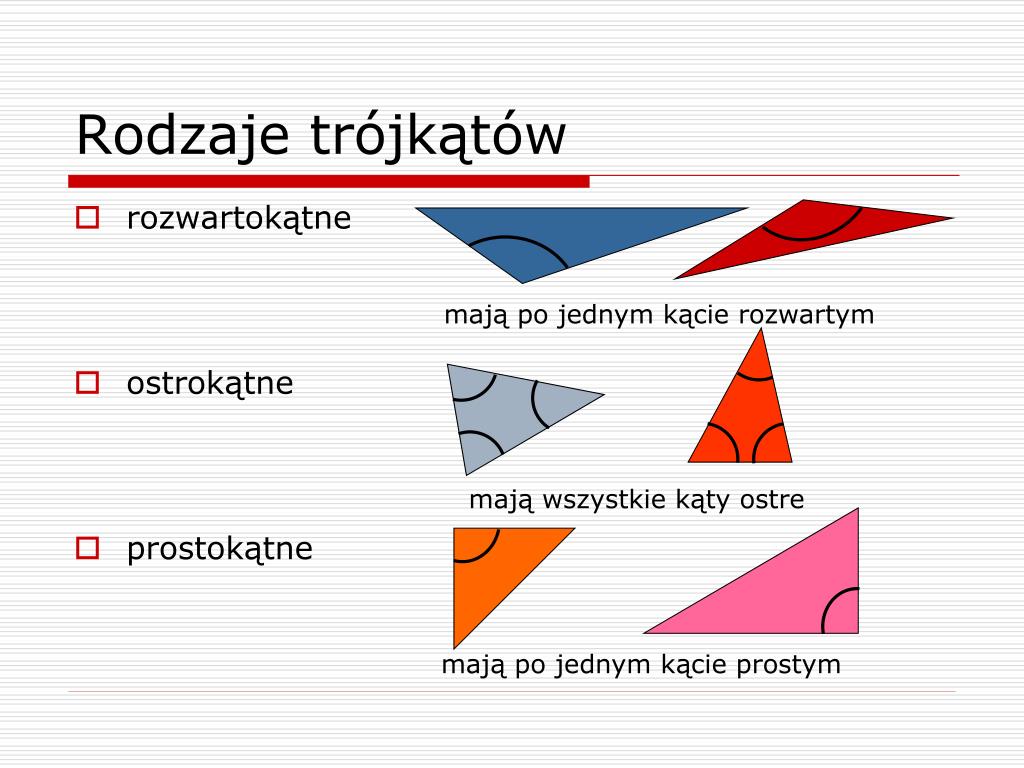
Trójkąt Ostrokątny: Posiada wszystkie trzy kąty ostre (mniejsze niż 90 stopni).
Trójkąt Prostokątny: Posiada jeden kąt prosty (90 stopni). Bok naprzeciwko kąta prostego nazywamy przeciwprostokątną, a pozostałe dwa boki to przyprostokątne. To właśnie w tym trójkącie obowiązuje słynne twierdzenie Pitagorasa: a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej.
Trójkąt Rozwartokątny: Posiada jeden kąt rozwarty (większy niż 90 stopni).

Ważne Własności Trójkątów

Suma Kątów w Trójkącie: Niezależnie od rodzaju trójkąta, suma miar jego kątów wewnętrznych zawsze wynosi 180 stopni. Pamiętaj o tym! To bardzo przydatne!
Nierówność Trójkąta: Suma długości dwóch dowolnych boków trójkąta musi być większa niż długość trzeciego boku. Inaczej nie da się takiego trójkąta zbudować!
Wysokość Trójkąta: To odcinek łączący wierzchołek trójkąta z prostą zawierającą przeciwległy bok (lub jego przedłużenie) i padający na tę prostą pod kątem prostym. Każdy trójkąt ma trzy wysokości.

Pole Trójkąta

Aby obliczyć pole trójkąta, najczęściej używamy wzoru:

P = (1/2) * a * h

gdzie:

P to pole trójkąta,
a to długość podstawy trójkąta,
h to długość wysokości opuszczonej na tę podstawę.

Jeśli znamy długości wszystkich trzech boków trójkąta, możemy obliczyć jego pole, korzystając ze wzoru Herona:

P = √(s(s - a)(s - b)(s - c))

gdzie:

P to pole trójkąta,
a, b, c to długości boków trójkąta,
s to połowa obwodu trójkąta (s = (a + b + c) / 2).

Czworokąty – Różnorodność Form

Czworokąt to figura geometryczna, która ma cztery boki i cztery kąty. Podobnie jak w przypadku trójkątów, istnieje wiele różnych rodzajów czworokątów.

Rodzaje Czworokątów

Równoległobok: To czworokąt, który ma dwie pary boków równoległych. Przeciwległe boki równoległoboku są równe, a przeciwległe kąty są równe.
Prostokąt: To równoległobok, który ma wszystkie kąty proste.
Kwadrat: To prostokąt, który ma wszystkie boki równe. Jest to najbardziej "regularny" typ czworokąta.
Romb: To równoległobok, który ma wszystkie boki równe.
Trapez: To czworokąt, który ma przynajmniej jedną parę boków równoległych (podstawy). Pozostałe dwa boki (ramiona) mogą być równe (trapez równoramienny) lub różne (trapez różnoboczny). Szczególnym przypadkiem trapezu jest trapez prostokątny, który ma co najmniej jeden kąt prosty.
Deltoid: To czworokąt, który ma dwie pary sąsiednich boków równych. Przekątne deltoidu przecinają się pod kątem prostym.

Ważne Własności Czworokątów

Suma Kątów w Czworokącie: Suma miar kątów wewnętrznych w każdym czworokącie wynosi 360 stopni.
Przekątne w Czworokątach: Przekątne to odcinki łączące przeciwległe wierzchołki czworokąta. Ich właściwości zależą od rodzaju czworokąta. Na przykład, w prostokącie przekątne są równe i przecinają się w połowie, a w kwadracie przekątne są równe, przecinają się w połowie i są prostopadłe.

Pole Czworokątów

Wzory na pole czworokątów zależą od ich rodzaju:

Pole Równoległoboku: P = a * h, gdzie a to długość podstawy, a h to długość wysokości opuszczonej na tę podstawę.
Pole Prostokąta: P = a * b, gdzie a i b to długości boków prostokąta.
Pole Kwadratu: P = a², gdzie a to długość boku kwadratu.
Pole Rombu: P = (1/2) * d₁ * d₂, gdzie d₁ i d₂ to długości przekątnych rombu. Można też użyć wzoru P = a * h, gdzie a to długość boku, a h to długość wysokości opuszczonej na ten bok.
Pole Trapezu: P = (1/2) * (a + b) * h, gdzie a i b to długości podstaw trapezu, a h to długość wysokości trapezu.
Pole Deltoidu: P = (1/2) * d₁ * d₂, gdzie d₁ i d₂ to długości przekątnych deltoidu.

Przykłady i Zastosowania

Wszystkie te pojęcia i wzory mogą wydawać się abstrakcyjne, ale geometria jest wszędzie wokół nas! Spójrz na budynki – są pełne trójkątów i czworokątów! Dach domu to często trójkąt, okna to najczęściej prostokąty lub kwadraty. Podczas projektowania mebli, budowania domów, a nawet w grach komputerowych, wiedza o trójkątach i czworokątach jest niezbędna. Pomyśl o boisku do piłki nożnej - to w gruncie rzeczy duży prostokąt! A piramidy w Egipcie? To w gruncie rzeczy trójkąty połączone w przestrzeni.

Weźmy przykład: Chcesz obliczyć pole trawnika w kształcie trapezu. Mierzysz jego podstawy – jedna ma 5 metrów, druga 7 metrów. Wysokość trapezu wynosi 4 metry. Używasz wzoru na pole trapezu: P = (1/2) * (5 + 7) * 4 = (1/2) * 12 * 4 = 24 metry kwadratowe. Wiesz już, że potrzebujesz 24 metry kwadratowe trawy, żeby pokryć cały trawnik!

Podsumowanie i Co Dalej?

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć trójkąty i czworokąty. Pamiętaj, że kluczem do sukcesu w geometrii jest praktyka! Rozwiązuj zadania, rysuj figury i staraj się dostrzegać geometrię w otaczającym Cię świecie. Ćwiczenie czyni mistrza!

Co możesz zrobić dalej? Zajrzyj do swojego podręcznika, poszukaj dodatkowych zadań online, a może nawet spróbuj stworzyć własne figury geometryczne z papieru. Geometria to fascynująca dziedzina wiedzy, która rozwija logiczne myślenie i wyobraźnię przestrzenną. Wykorzystaj tę wiedzę w praktyce, a zobaczysz, jak wiele korzyści możesz z niej czerpać.

Powodzenia w dalszej nauce geometrii! Pamiętaj, matematyka może być przyjemna!