Trojkaty 30 60 90 Zadania

Czy kiedykolwiek patrzyłeś na trójkąt i czułeś się zagubiony? A może podczas rozwiązywania zadań z geometrii natrafiałeś na tajemnicze trójkąty o kątach 30, 60 i 90 stopni i nie wiedziałeś, jak się za nie zabrać? Jeśli tak, to ten artykuł jest właśnie dla Ciebie. Zrozumiem Twoje obawy. Geometria, a zwłaszcza trójkąty, potrafią być trudne, ale obiecuję, że po przeczytaniu tego tekstu, trójkąty 30-60-90 nie będą już stanowić problemu.

Czym Jest Trójkąt 30-60-90?

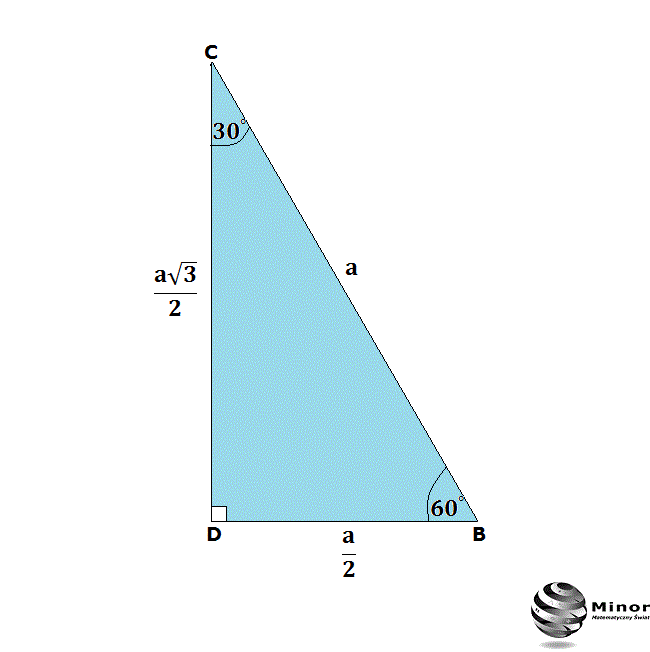
Trójkąt 30-60-90 to specjalny rodzaj trójkąta prostokątnego, w którym miary kątów wynoszą 30, 60 i 90 stopni. To, co czyni go wyjątkowym, to fakt, że stosunek długości jego boków jest zawsze taki sam. Dzięki temu możemy rozwiązywać wiele zadań, znając tylko długość jednego z boków.

Wyobraź sobie trójkąt równoboczny. Teraz przetnij go na pół, prowadząc linię od jednego wierzchołka do środka przeciwległego boku. Powstały trójkąt to właśnie nasz trójkąt 30-60-90! Ten obrazek mentalny pomoże Ci zapamiętać jego charakterystyczne cechy.

Kluczowe Właściwości Trójkąta 30-60-90

Aby skutecznie rozwiązywać zadania z trójkątami 30-60-90, musimy zrozumieć stosunki między długościami jego boków:

Najkrótszy bok (naprzeciw kąta 30 stopni): Oznaczmy go jako a.
Średni bok (naprzeciw kąta 60 stopni): Jego długość wynosi a√3.
Przeciwprostokątna (naprzeciw kąta 90 stopni): Jej długość wynosi 2a.

Te zależności są kluczowe. Zapamiętanie ich pozwoli Ci z łatwością obliczać długości boków w zadaniach.

Jak Rozwiązywać Zadania z Trójkątami 30-60-90?

Teraz przejdźmy do praktyki. Pokażę Ci krok po kroku, jak rozwiązywać typowe zadania z tymi trójkątami.

Krok 1: Zidentyfikuj Trójkąt 30-60-90

Upewnij się, że trójkąt rzeczywiście ma kąty 30, 60 i 90 stopni. Czasami zadania są podchwytliwe i wyglądają na trójkąty 30-60-90, ale nimi nie są.

Krok 2: Zidentyfikuj Znany Bok

Sprawdź, który bok ma podaną długość. Czy to najkrótszy bok, średni bok, czy przeciwprostokątna?

Krok 3: Zastosuj Odpowiednie Stosunki

W zależności od tego, który bok jest znany, użyj odpowiedniego wzoru, aby obliczyć długości pozostałych boków:

Jeśli znasz najkrótszy bok (a):
- Średni bok = a√3
- Przeciwprostokątna = 2a
Jeśli znasz średni bok (a√3):
- Najkrótszy bok = a = (a√3) / √3
- Przeciwprostokątna = 2a = 2 * ((a√3) / √3)
Jeśli znasz przeciwprostokątną (2a):
- Najkrótszy bok = a = (2a) / 2
- Średni bok = a√3 = ((2a) / 2) * √3

Przykład 1: Znany Najkrótszy Bok

Załóżmy, że najkrótszy bok trójkąta 30-60-90 ma długość 5 cm. Oblicz długość pozostałych boków.

Rozwiązanie:

Najkrótszy bok (a) = 5 cm
Średni bok = a√3 = 5√3 cm
Przeciwprostokątna = 2a = 2 * 5 = 10 cm

Przykład 2: Znany Średni Bok

Załóżmy, że średni bok trójkąta 30-60-90 ma długość 8√3 cm. Oblicz długość pozostałych boków.

Rozwiązanie:

Średni bok (a√3) = 8√3 cm
Najkrótszy bok = a = (8√3) / √3 = 8 cm
Przeciwprostokątna = 2a = 2 * 8 = 16 cm

Przykład 3: Znana Przeciwprostokątna

Załóżmy, że przeciwprostokątna trójkąta 30-60-90 ma długość 12 cm. Oblicz długość pozostałych boków.

Rozwiązanie:

Przeciwprostokątna (2a) = 12 cm
Najkrótszy bok = a = 12 / 2 = 6 cm
Średni bok = a√3 = 6√3 cm

Praktyczne Wskazówki i Triki

Oto kilka dodatkowych wskazówek, które pomogą Ci w rozwiązywaniu zadań z trójkątami 30-60-90:

Rysuj! Zawsze narysuj trójkąt. Wizualizacja zadania ułatwia zrozumienie i rozwiązanie.
Oznaczaj! Oznacz boki trójkąta literami a, a√3 i 2a, aby uniknąć pomyłek.
Używaj twierdzenia Pitagorasa jako sprawdzenia. Po obliczeniu wszystkich boków, możesz sprawdzić, czy spełniają one równanie a² + b² = c², gdzie a i b to przyprostokątne, a c to przeciwprostokątna.
Pamiętaj o jednostkach! Zawsze podawaj jednostki długości (cm, m, itd.) w swoich odpowiedziach.
Ćwicz! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady i szybciej będziesz w stanie rozwiązywać trudniejsze problemy.

Zastosowania Trójkątów 30-60-90 w Życiu Codziennym

Trójkąty 30-60-90 nie są tylko abstrakcyjnymi figurami geometrycznymi. Mają one wiele praktycznych zastosowań w różnych dziedzinach, takich jak:

Architektura: Projektowanie budynków, dachów i innych konstrukcji.
Inżynieria: Obliczanie sił i obciążeń w konstrukcjach.
Nawigacja: Wyznaczanie kursów i odległości.
Stolarstwo: Wykonywanie precyzyjnych cięć i połączeń.
Gry komputerowe: Tworzenie realistycznych środowisk 3D.

Na przykład, inżynier może wykorzystać właściwości trójkąta 30-60-90 do obliczenia, pod jakim kątem nachylenia należy zbudować rampę, aby była ona bezpieczna i wygodna w użytkowaniu.

Podsumowanie

Trójkąty 30-60-90 to fascynujące figury geometryczne, które, choć początkowo mogą wydawać się skomplikowane, kryją w sobie prostą i elegancką logikę. Pamiętając o stosunkach między długościami ich boków i stosując się do przedstawionych wskazówek, możesz z łatwością rozwiązywać zadania z nimi związane. Nie bój się ćwiczyć i eksperymentować! Im więcej czasu poświęcisz na rozwiązywanie zadań, tym pewniej będziesz się czuł z tym tematem. Pamiętaj, że geometria to nie tylko zbiór wzorów, ale także sposób myślenia i rozwiązywania problemów.

Powodzenia w dalszej nauce geometrii! I pamiętaj, że trójkąt 30-60-90 to Twój przyjaciel!