Trójkąt Szczególny 30 60 90

Czy kiedykolwiek czułeś się zagubiony, próbując rozwiązać zadanie z geometrii, w którym pojawia się trójkąt, a Ty nie masz pojęcia, od czego zacząć? Zapewne tak. Wiele osób zmaga się z tymi samymi trudnościami, szczególnie gdy chodzi o trójkąty szczególne. One często wydają się skomplikowane i abstrakcyjne, ale tak naprawdę są one kluczem do wielu problemów matematycznych i mają zastosowanie w wielu dziedzinach życia. Spróbujemy rozłożyć problem trójkąta 30-60-90 na czynniki pierwsze, wyjaśniając krok po kroku, dlaczego jest on tak ważny i jak go efektywnie wykorzystywać.

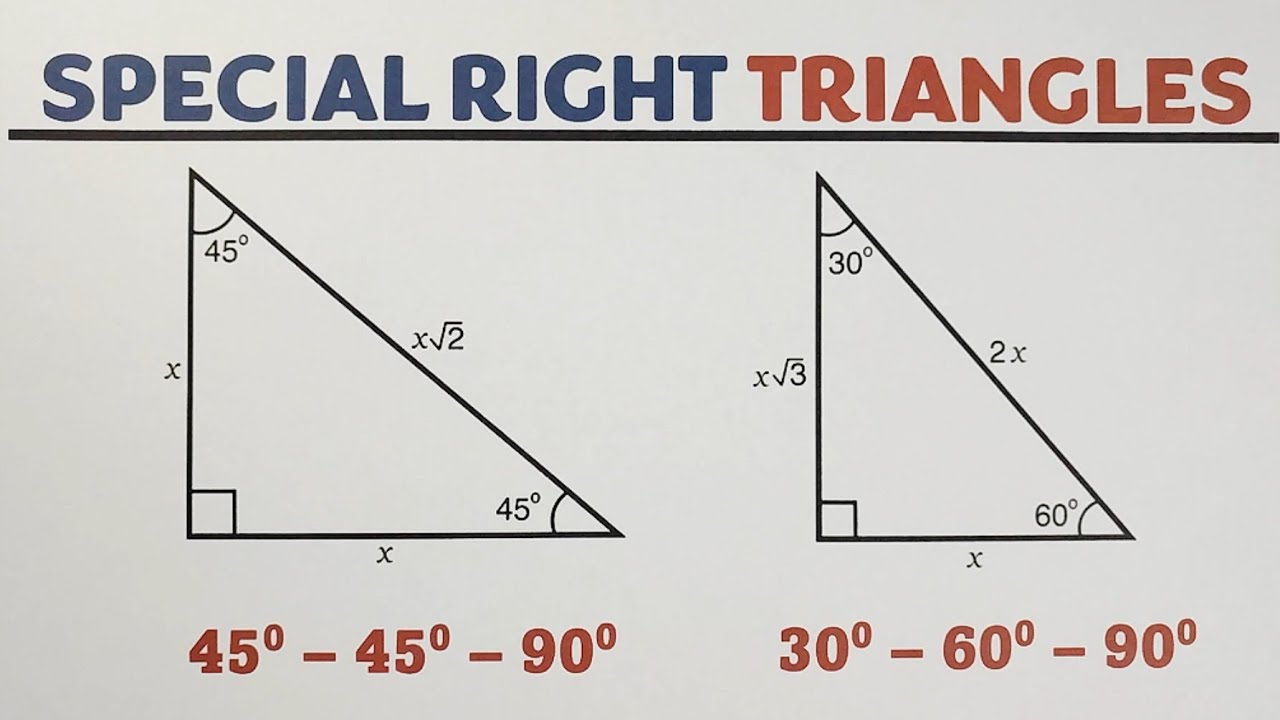
Czym Jest Trójkąt Szczególny 30-60-90?

Trójkąt szczególny 30-60-90, jak sama nazwa wskazuje, to trójkąt prostokątny, którego kąty wewnętrzne mają miary 30, 60 i 90 stopni. To właśnie te specyficzne kąty nadają mu unikalne właściwości i sprawiają, że jest on tak użyteczny. Jego boki mają ustalone proporcje, co znacznie ułatwia obliczenia.

Podstawowe Właściwości

• Kąty: 30°, 60°, 90°
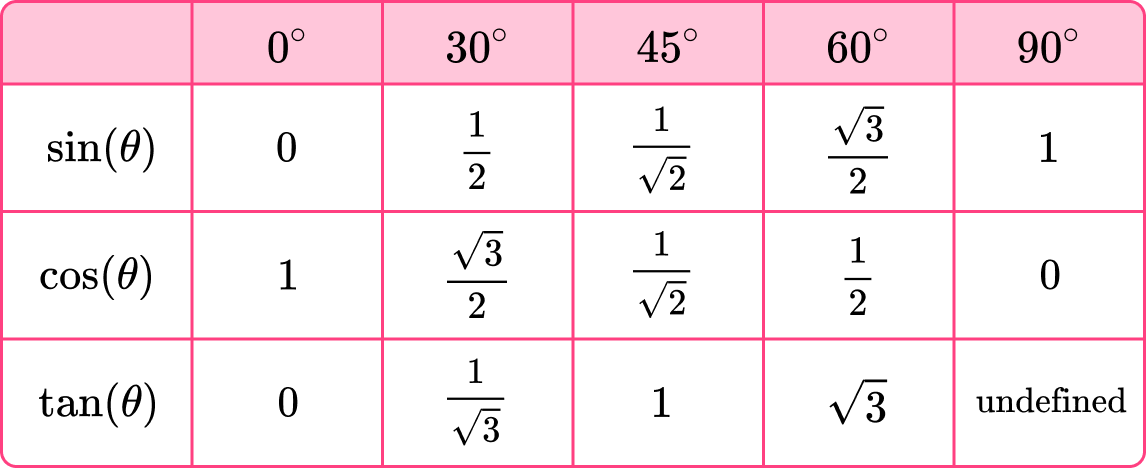
• Stosunek Boków: Najkrótsza przyprostokątna (naprzeciw kąta 30°) : Druga przyprostokątna (naprzeciw kąta 60°) : Przeciwprostokątna = 1 : √3 : 2

To oznacza, że jeśli znamy długość jednego z boków trójkąta 30-60-90, możemy bez problemu obliczyć długości pozostałych boków, wykorzystując powyższy stosunek. Jest to znacznie prostsze niż korzystanie z bardziej skomplikowanych funkcji trygonometrycznych, szczególnie na początku nauki geometrii.

Dlaczego Trójkąt 30-60-90 Jest Tak Ważny?

Możesz się zastanawiać, dlaczego poświęcamy tyle uwagi akurat temu konkretnemu trójkątowi. Otóż, jest on niezwykle popularny w zadaniach z geometrii i trygonometrii, pojawia się często na egzaminach (matura, testy kompetencji) i jest fundamentem do zrozumienia bardziej zaawansowanych zagadnień. Poza tym, ma realne zastosowania w wielu dziedzinach:

• Architektura i Budownictwo: Projektowanie dachów, konstrukcji, pomiary terenowe.
• Inżynieria: Obliczenia konstrukcyjne, projektowanie maszyn.
• Grafika Komputerowa i Gry: Obliczenia perspektywy, modelowanie 3D.
• Fizyka: Rozkład sił, analiza ruchu.

Wyobraź sobie architekta projektującego dach. Znajomość własności trójkąta 30-60-90 pozwala mu szybko i precyzyjnie obliczyć kąty nachylenia i długości krokwi, zapewniając stabilność i estetykę konstrukcji. Podobnie, w grach komputerowych, wykorzystanie tego trójkąta pozwala na realistyczne odwzorowanie perspektywy i ruchu obiektów.

Jak Rozwiązywać Zadania z Trójkątem 30-60-90?

Kluczem do sukcesu jest rozpoznanie trójkąta 30-60-90 w zadaniu i zastosowanie odpowiednich proporcji. Oto kilka kroków, które pomogą Ci w rozwiązywaniu problemów:

1. Zidentyfikuj Trójkąt: Upewnij się, że masz do czynienia z trójkątem prostokątnym o kątach 30° i 60°.
2. Określ Znany Bok: Zidentyfikuj, który bok znasz (najkrótsza przyprostokątna, druga przyprostokątna, przeciwprostokątna).
3. Wykorzystaj Proporcje: Zastosuj proporcje 1 : √3 : 2, aby obliczyć długości pozostałych boków.

Przykładowe Zadanie

Załóżmy, że w trójkącie 30-60-90 najkrótsza przyprostokątna (naprzeciw kąta 30°) ma długość 5 cm. Jakie są długości pozostałych boków?

1. Znany Bok: Najkrótsza przyprostokątna = 5 cm.
2. Proporcje: 1 : √3 : 2
3. Obliczenia:
   • Druga przyprostokątna = 5 * √3 cm ≈ 8.66 cm
   • Przeciwprostokątna = 5 * 2 cm = 10 cm

Widzimy, że znając tylko jeden bok, możemy z łatwością obliczyć pozostałe. To właśnie czyni ten trójkąt tak praktycznym.

Kontrargumenty i Częste Błędy

Oczywiście, niektórzy mogą argumentować, że w erze kalkulatorów i programów komputerowych znajomość własności trójkąta 30-60-90 nie jest już tak istotna. Można użyć funkcji trygonometrycznych lub narzędzi CAD, aby rozwiązać te same problemy. Jednak znajomość podstawowych zasad geometrii, w tym własności trójkąta 30-60-90, daje intuicję i głębsze zrozumienie zagadnień. Pozwala na szybkie szacowanie wyników i weryfikację poprawności obliczeń wykonanych przez programy komputerowe.

Częstym błędem jest pomylenie boków naprzeciw kątów. Pamiętaj, że najkrótsza przyprostokątna zawsze leży naprzeciw kąta 30°, a druga przyprostokątna naprzeciw kąta 60°. Błędne zidentyfikowanie boków prowadzi do niepoprawnych obliczeń.

Rozwiązania i Dalsze Kroki

Jak zatem uniknąć błędów i opanować umiejętność rozwiązywania zadań z trójkątem 30-60-90? Najlepszym rozwiązaniem jest praktyka! Rozwiązuj jak najwięcej zadań, zacznij od prostych, a stopniowo przechodź do bardziej skomplikowanych. Korzystaj z podręczników, zbiorów zadań, internetowych zasobów. Zwracaj uwagę na szczegóły i dokładnie analizuj każdy krok rozwiązania. Nie bój się pytać, jeśli masz wątpliwości. Pamiętaj, że regularne ćwiczenia przynoszą najlepsze rezultaty.

Oprócz ćwiczeń, warto również zapamiętać wzory na pola i obwody trójkąta 30-60-90. Znając długość jednego z boków, można łatwo obliczyć pozostałe wielkości.

Dodatkowo, rozważ skorzystanie z wizualizacji. Narysuj kilka trójkątów 30-60-90 o różnych wymiarach i zaznacz proporcje boków. Możesz również użyć programów do geometrii dynamicznej, aby interaktywnie badać własności tego trójkąta.

Podsumowanie

Trójkąt szczególny 30-60-90 to potężne narzędzie, które może znacznie ułatwić rozwiązywanie problemów geometrycznych i trygonometrycznych. Jego unikalne właściwości i proste proporcje pozwalają na szybkie i precyzyjne obliczenia. Znajomość tego trójkąta jest nie tylko przydatna w szkole, ale również w wielu dziedzinach życia, takich jak architektura, inżynieria czy grafika komputerowa. Pamiętaj, że kluczem do sukcesu jest praktyka i regularne ćwiczenia.

Czy czujesz się teraz pewniej, patrząc na trójkąt 30-60-90? Jak wykorzystasz nowo zdobytą wiedzę w rozwiązywaniu zadań z geometrii?