Trojkat Rownoramienny Wzor Na Pole
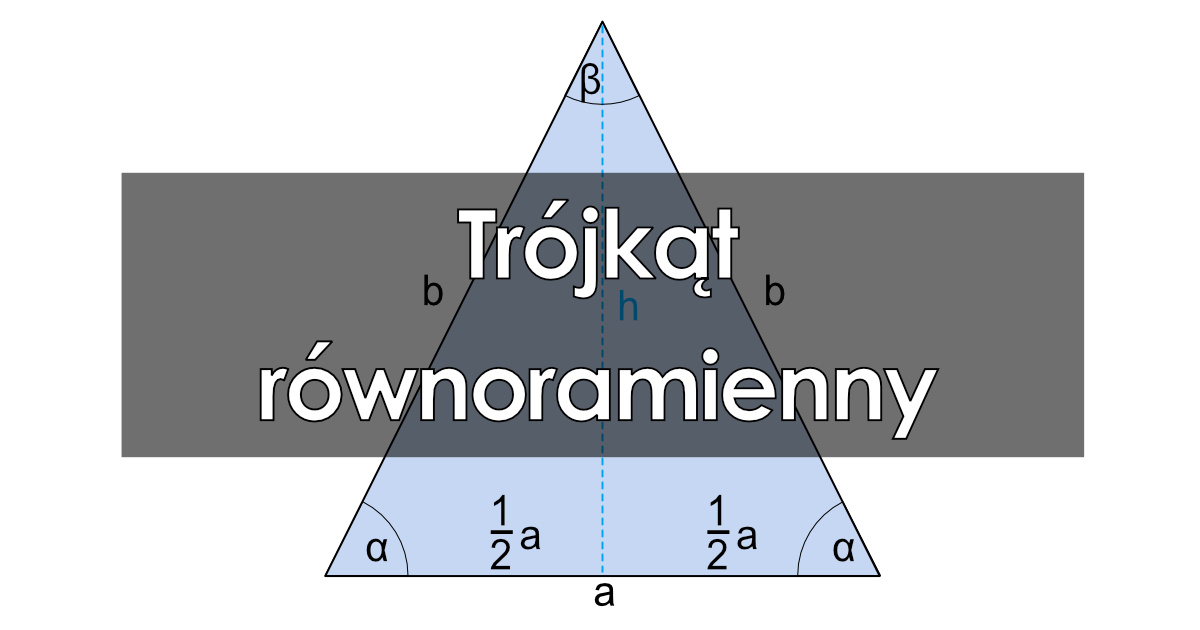
W geometrii euklidesowej, trójkąt równoramienny zajmuje szczególne miejsce. Charakteryzuje się posiadaniem co najmniej dwóch boków równej długości, co wpływa na jego właściwości i sposób obliczania jego pola. Znajomość wzoru na pole trójkąta równoramiennego jest fundamentalna dla wielu dziedzin, od architektury po inżynierię.
Podstawowe Właściwości Trójkąta Równoramiennego
Zanim przejdziemy do wzorów na pole, warto przypomnieć kluczowe cechy trójkąta równoramiennego:
- Dwa boki są równe (ramiona).
- Dwa kąty przy podstawie są równe.
- Wysokość opuszczona na podstawę dzieli ją na dwie równe części i jest jednocześnie środkową oraz dwusieczną kąta wierzchołkowego.
Różne Wzory na Pole Trójkąta Równoramiennego
Istnieje kilka sposobów obliczenia pola trójkąta równoramiennego, w zależności od danych, które posiadamy. Omówimy te najbardziej popularne:
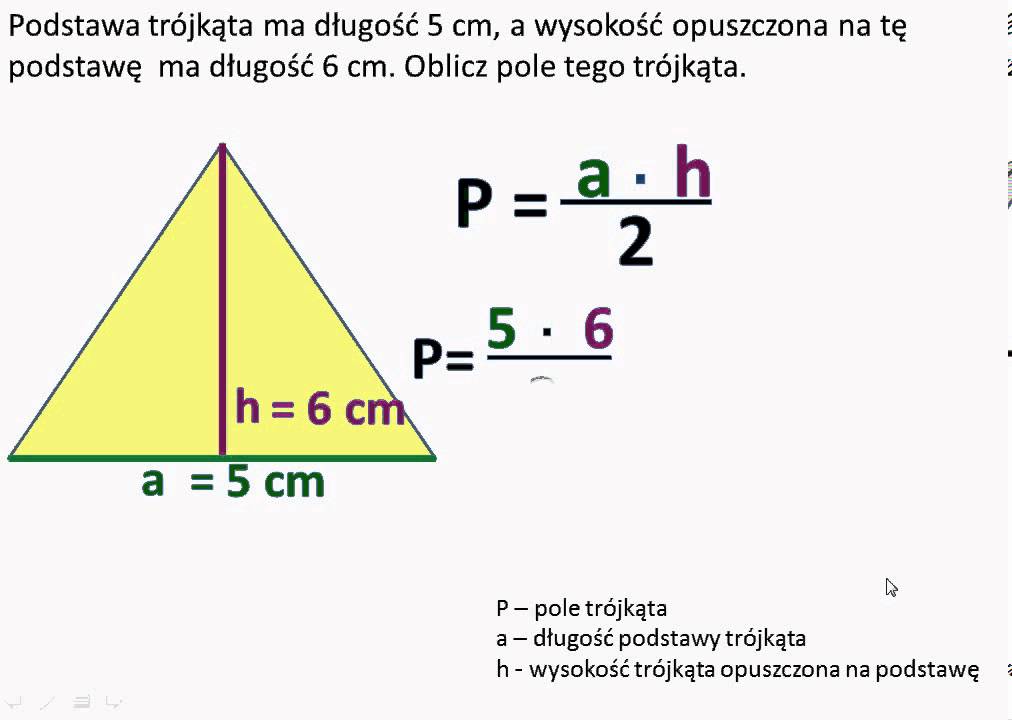
1. Wzór Podstawowy: Pole = (1/2) * podstawa * wysokość
Ten wzór jest uniwersalny dla wszystkich trójkątów, w tym równoramiennych. Jeśli znamy długość podstawy (oznaczmy ją jako a) i wysokość opuszczoną na tę podstawę (oznaczmy ją jako h), to pole (P) możemy obliczyć następująco:
P = (1/2) * a * h
Przykład: Jeżeli podstawa trójkąta równoramiennego ma długość 10 cm, a wysokość opuszczona na tę podstawę wynosi 8 cm, to pole wynosi:
P = (1/2) * 10 cm * 8 cm = 40 cm2
2. Wzór z Użyciem Długości Ramienia i Kąta
Jeśli znamy długość ramienia (oznaczmy ją jako b) i kąt między ramionami (kąt wierzchołkowy, oznaczmy go jako α), możemy użyć następującego wzoru:
P = (1/2) * b2 * sin(α)
Ten wzór wykorzystuje funkcję sinus, co wymaga pewnej wiedzy z trygonometrii. α musi być podane w stopniach lub radianach, w zależności od ustawień kalkulatora.
Przykład: Załóżmy, że ramię trójkąta równoramiennego ma długość 6 cm, a kąt między ramionami wynosi 30 stopni. Wtedy:
P = (1/2) * 62 cm2 * sin(30°) = (1/2) * 36 cm2 * 0.5 = 9 cm2
3. Wzór z Użyciem Długości Ramienia i Kąta przy Podstawie
Jeśli znamy długość ramienia (b) i kąt przy podstawie (oznaczmy go jako β), to możemy wykorzystać związek trygonometryczny do wyznaczenia wysokości, a następnie obliczyć pole. Kąt przy podstawie jest równy połowie różnicy między 180 stopni a kątem wierzchołkowym: β = (180° - α) / 2. Alternatywnie, można bezpośrednio użyć wzoru:
P = b2 * sin(β) * cos(β)
lub, co jest równoważne:
P = (1/2) * b2 * sin(2β)
Przykład: Jeśli ramię trójkąta ma długość 7 cm, a kąt przy podstawie wynosi 45 stopni, to:
P = 72 cm2 * sin(45°) * cos(45°) = 49 cm2 * (√2/2) * (√2/2) = 49 cm2 * (1/2) = 24.5 cm2
4. Wzór Herona (Możliwość Zastosowania)
Chociaż wzór Herona jest zwykle stosowany do trójkątów różnobocznych, można go również użyć do trójkątów równoramiennych. Wzór ten wymaga znajomości długości wszystkich trzech boków. Dla trójkąta równoramiennego o ramionach długości b i podstawie długości a, semi-perymetr (s) wynosi:
s = (a + b + b) / 2 = (a + 2b) / 2
Wzór Herona na pole (P) to:
P = √[s(s - a)(s - b)(s - b)]
Przykład: Załóżmy, że podstawa trójkąta równoramiennego ma długość 8 cm, a ramiona mają długość 5 cm. Wtedy:
s = (8 + 5 + 5) / 2 = 9 cm
P = √[9(9 - 8)(9 - 5)(9 - 5)] = √[9 * 1 * 4 * 4] = √144 = 12 cm2
Praktyczne Zastosowania
Wzory na pole trójkąta równoramiennego mają szerokie zastosowanie w różnych dziedzinach:
- Architektura i Budownictwo: Obliczanie powierzchni dachów, ścian i innych elementów konstrukcyjnych. Projektowanie elementów dekoracyjnych.
- Inżynieria: Obliczanie obciążeń i stabilności konstrukcji trójkątnych. Analiza sił działających na elementy konstrukcyjne w mostach i kratownicach.
- Geodezja i Kartografia: Pomiar powierzchni działek o nieregularnych kształtach. Wyznaczanie odległości i wysokości w terenie.
- Projektowanie Graficzne: Tworzenie logo i ikon wykorzystujących kształt trójkąta. Obliczanie powierzchni elementów w projektach.
- Stolarstwo: Wycinanie elementów mebli i konstrukcji drewnianych. Obliczanie ilości materiału potrzebnego do wykonania projektu.
Na przykład, przy projektowaniu dachu w kształcie trójkąta równoramiennego, architekt musi precyzyjnie obliczyć jego powierzchnię, aby oszacować ilość potrzebnych materiałów (dachówek, blachy itp.) oraz koszty. Inżynierowie budujący mosty kratownicowe wykorzystują trójkąty równoramienne ze względu na ich stabilność i odporność na obciążenia. Zrozumienie właściwości i umiejętność obliczania pola trójkąta równoramiennego jest kluczowe w tych zastosowaniach.
Typowe Błędy Przy Obliczaniu Pola
Przy obliczaniu pola trójkąta równoramiennego, warto unikać następujących błędów:
- Pomylenie jednostek: Upewnij się, że wszystkie wymiary są podane w tej samej jednostce (np. cm, m).
- Użycie nieodpowiedniej wysokości: Wysokość musi być prostopadła do podstawy, na którą jest opuszczona.
- Błędy w kalkulacjach trygonometrycznych: Upewnij się, że kalkulator jest ustawiony na odpowiedni tryb (stopnie lub radiany).
- Niewłaściwe zastosowanie wzoru Herona: Pamiętaj o obliczeniu semi-perymetru.
Podsumowanie
Znajomość wzoru na pole trójkąta równoramiennego jest niezbędna w wielu dziedzinach. W zależności od dostępnych danych, możemy stosować różne wzory, aby obliczyć pole. Pamiętaj o prawidłowym stosowaniu jednostek i unikaniu typowych błędów. Ćwiczenie obliczeń na różnych przykładach pomoże utrwalić wiedzę i zwiększyć pewność w rozwiązywaniu problemów geometrycznych.
Zachęcamy do rozwiązywania zadań związanych z polem trójkąta równoramiennego i eksperymentowania z różnymi wzorami. Wykorzystaj tę wiedzę w praktyce, analizując obiekty i konstrukcje w swoim otoczeniu. Powodzenia!