Trojkat Rownoboczny Wzor Na Pole

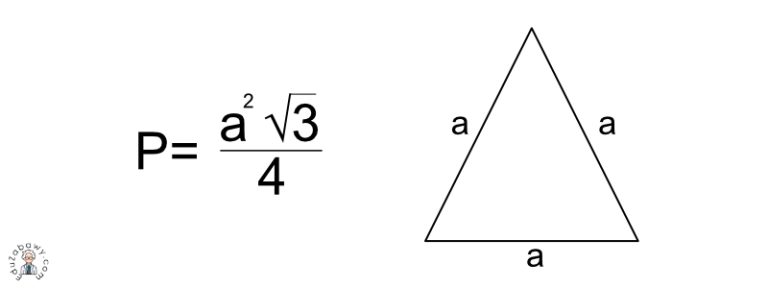
W geometrii, trójkąt równoboczny zajmuje wyjątkowe miejsce. Jego regularna struktura i symetria sprawiają, że jest on nie tylko elegancki wizualnie, ale również fundamentalny w wielu obliczeniach i zastosowaniach. Zrozumienie wzoru na pole trójkąta równobocznego jest kluczowe dla każdego, kto zajmuje się matematyką, fizyką, inżynierią, czy nawet sztuką i architekturą.

Dlaczego trójkąt równoboczny jest taki ważny?

Trójkąt równoboczny charakteryzuje się trzema równymi bokami i trzema równymi kątami, każdy mierzący 60 stopni. Ta doskonała symetria przekłada się na wiele praktycznych zastosowań. Jest on podstawą wielu konstrukcji geometrycznych, stanowi element składowy bardziej złożonych figur, a jego właściwości są wykorzystywane w optyce, mechanice i innych dziedzinach nauki i techniki.

Wszechstronność i zastosowania trójkąta równobocznego

Od mozaik i parkietaży, po projektowanie mostów i konstrukcje kratowe – trójkąty równoboczne pojawiają się wszędzie. Ich sztywność i stabilność czynią je idealnymi do budowy struktur wymagających dużej wytrzymałości. W architekturze często wykorzystuje się trójkątne moduły do tworzenia geometrycznie interesujących fasad i dachów. W inżynierii mechanicznej, analiza naprężeń w elementach o kształcie trójkątów równobocznych jest częstym zadaniem.

Wzór na pole trójkąta równobocznego: Szczegółowe omówienie

Wzór na pole trójkąta równobocznego to: P = (a² * √3) / 4, gdzie 'a' oznacza długość boku trójkąta. Jest to uproszczenie ogólnego wzoru na pole trójkąta: P = (1/2) * podstawa * wysokość, wynikające ze specyficznych właściwości trójkąta równobocznego.

Skąd się bierze ten wzór?

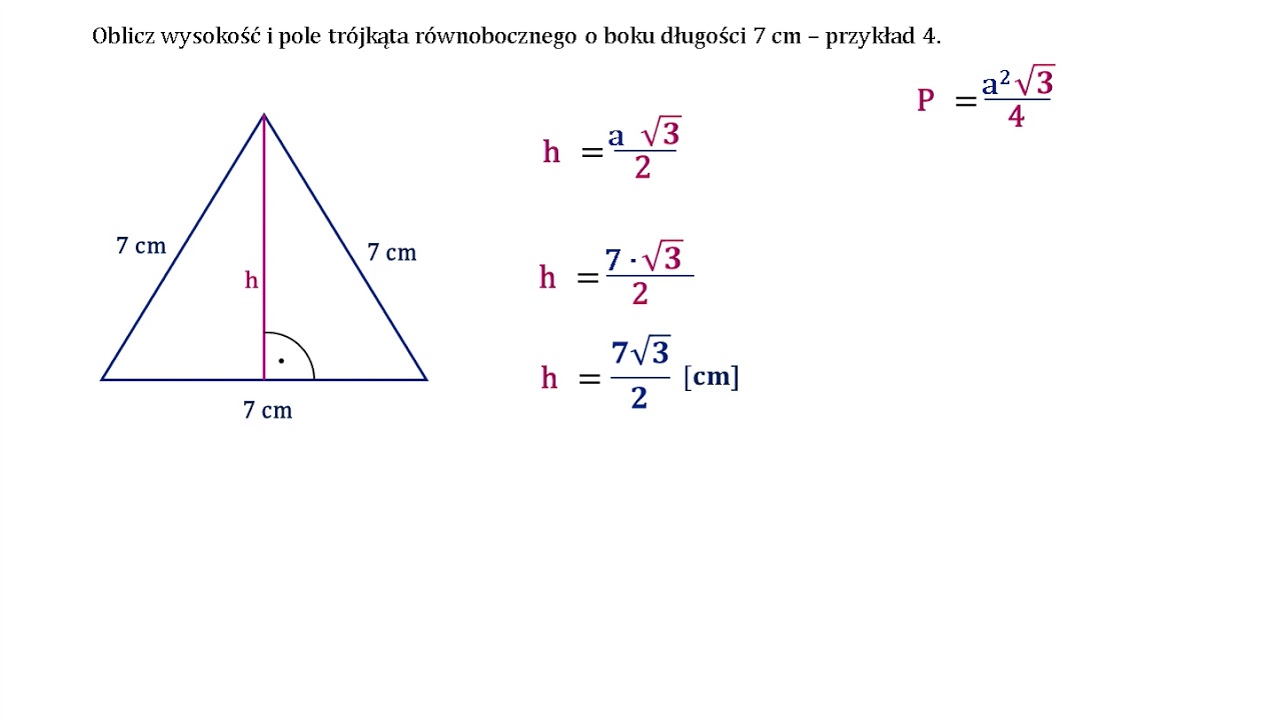
Aby zrozumieć pochodzenie wzoru, musimy przypomnieć sobie, jak oblicza się pole dowolnego trójkąta: P = (1/2) * b * h, gdzie 'b' to długość podstawy, a 'h' to wysokość. W trójkącie równobocznym, wysokość dzieli podstawę na dwie równe części i tworzy dwa trójkąty prostokątne. Możemy użyć twierdzenia Pitagorasa, aby wyrazić wysokość 'h' w zależności od długości boku 'a'.

Zatem, jeśli mamy trójkąt równoboczny o boku 'a', jego wysokość 'h' można obliczyć jako: h = √(a² - (a/2)²). Po uproszczeniu, otrzymujemy: h = (a√3) / 2.

Teraz, podstawiając tę wartość 'h' do ogólnego wzoru na pole trójkąta, otrzymujemy:

P = (1/2) * a * (a√3) / 2 = (a² * √3) / 4.

To dowodzi, że wzór P = (a² * √3) / 4 jest poprawny dla każdego trójkąta równobocznego.

Przykład obliczeniowy

Załóżmy, że mamy trójkąt równoboczny o boku a = 5 cm. Chcemy obliczyć jego pole. Używamy wzoru:

P = (a² * √3) / 4 = (5² * √3) / 4 = (25 * √3) / 4 ≈ 10.83 cm².

Zatem, pole tego trójkąta wynosi około 10.83 centymetrów kwadratowych.

Uproszczenia i alternatywne podejścia

Chociaż wzór P = (a² * √3) / 4 jest najczęściej używany, istnieją alternatywne metody obliczania pola trójkąta równobocznego, zwłaszcza gdy mamy dostępne inne dane, na przykład długość wysokości.

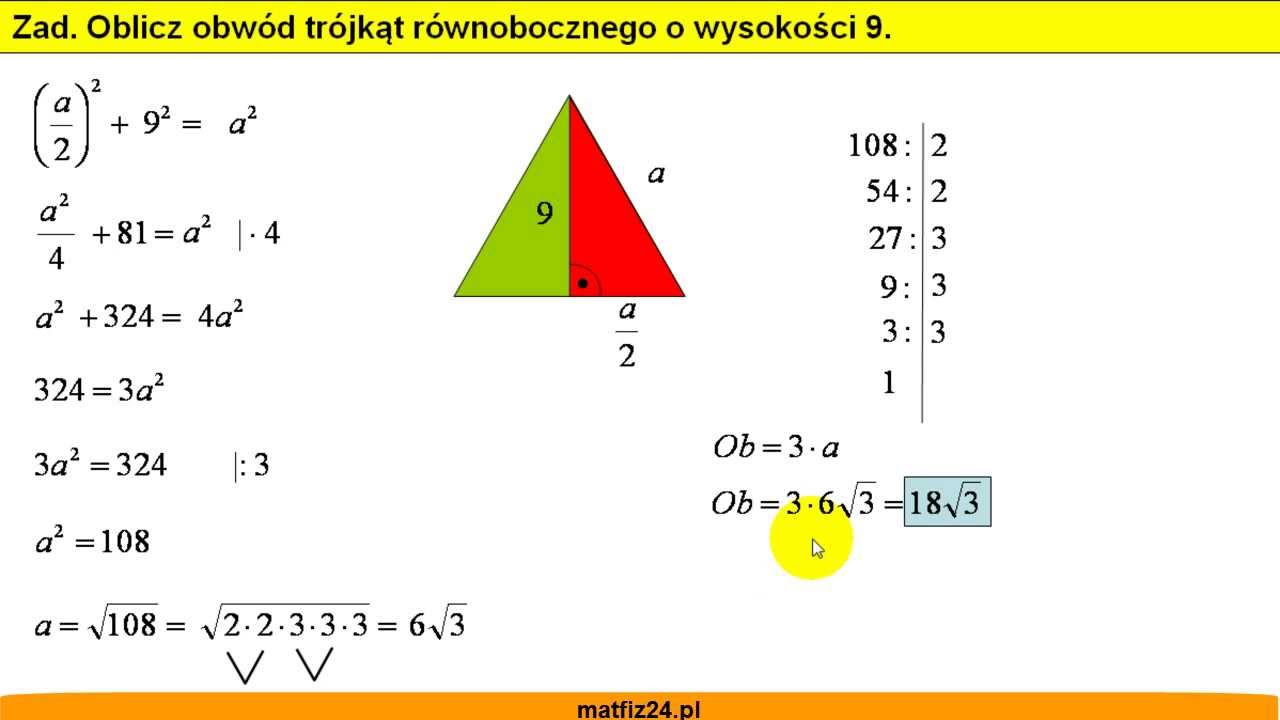
Wykorzystanie wysokości do obliczenia pola

Jak wspomniano wcześniej, wysokość trójkąta równobocznego wyraża się wzorem h = (a√3) / 2. Jeśli znamy wysokość 'h', możemy przekształcić ten wzór, aby znaleźć długość boku 'a':

a = (2h) / √3.

Następnie, podstawiając tę wartość 'a' do wzoru na pole, możemy obliczyć pole znając jedynie wysokość.

Znaczenie znajomości podstawowych wzorów

Pomimo istnienia różnych metod, znajomość podstawowego wzoru P = (a² * √3) / 4 jest niezwykle przydatna, ponieważ pozwala na szybkie i efektywne obliczanie pola trójkąta równobocznego, bazując wyłącznie na długości jego boku. Jest to fundamentalne narzędzie w wielu dziedzinach.

Real-world examples or data

Consider the design of a geodesic dome. These structures are often constructed using triangular panels, many of which are equilateral. Calculating the area of these panels is crucial for determining material requirements, structural load calculations, and overall cost estimation. Imagine a geodesic dome with 1000 equilateral triangular panels, each with a side length of 1 meter. The total surface area of the panels can be calculated as 1000 * (1² * √3) / 4 ≈ 433 square meters. This data is vital for purchasing materials and planning construction.

Another example is found in the design of mosaics. Many mosaic patterns incorporate equilateral triangles, creating visually appealing and mathematically precise designs. Artists and designers use the formula for the area of an equilateral triangle to precisely calculate the number of tiles required to fill a certain space. For instance, if an artist wants to create a mosaic featuring 500 equilateral triangle tiles, each with a side length of 2 centimeters, the total surface area covered by the mosaic would be 500 * (2² * √3) / 4 ≈ 866 square centimeters.

In the field of engineering, the analysis of stress distribution in triangular structures, such as bridge trusses, often involves calculations of area. These calculations are essential for ensuring the structural integrity and safety of the design. Accurate area calculations are critical for determining the forces acting on each element and for selecting appropriate materials.

Podsumowanie i wnioski

Wzór na pole trójkąta równobocznego, P = (a² * √3) / 4, jest fundamentalnym narzędziem w matematyce, geometrii i wielu dziedzinach praktycznych. Jego znajomość pozwala na efektywne obliczanie pola, a zrozumienie jego pochodzenia pogłębia wiedzę o właściwościach trójkąta równobocznego. Niezależnie od tego, czy jesteś studentem, inżynierem, architektem, czy po prostu osobą zainteresowaną geometrią, opanowanie tego wzoru przyniesie Ci wiele korzyści.

Zachęta do dalszej eksploracji

Zachęcam do dalszego zgłębiania wiedzy o geometrii i właściwościach trójkątów. Rozważ eksplorację innych typów trójkątów, ich zależności i zastosowań. Praktyczne ćwiczenia i rozwiązywanie zadań pomogą Ci utrwalić zdobytą wiedzę i rozwinąć umiejętność rozwiązywania problemów geometrycznych.

Pamiętaj, że matematyka jest fascynującą dziedziną, która otwiera drzwi do zrozumienia świata wokół nas. Wykorzystaj zdobytą wiedzę do kreatywnego rozwiązywania problemów i odkrywania nowych możliwości!