Trójkat Prostokątny Wzór Na Pole

W geometrii, trójkąt prostokątny odgrywa fundamentalną rolę. Jest to trójkąt, w którym jeden z kątów jest kątem prostym (90 stopni). Jego charakterystyczna budowa sprawia, że posiada on unikalne właściwości i liczne zastosowania w różnych dziedzinach nauki i życia codziennego. Jedną z kluczowych umiejętności związanych z trójkątem prostokątnym jest obliczanie jego pola.

Podstawowe definicje i cechy trójkąta prostokątnego

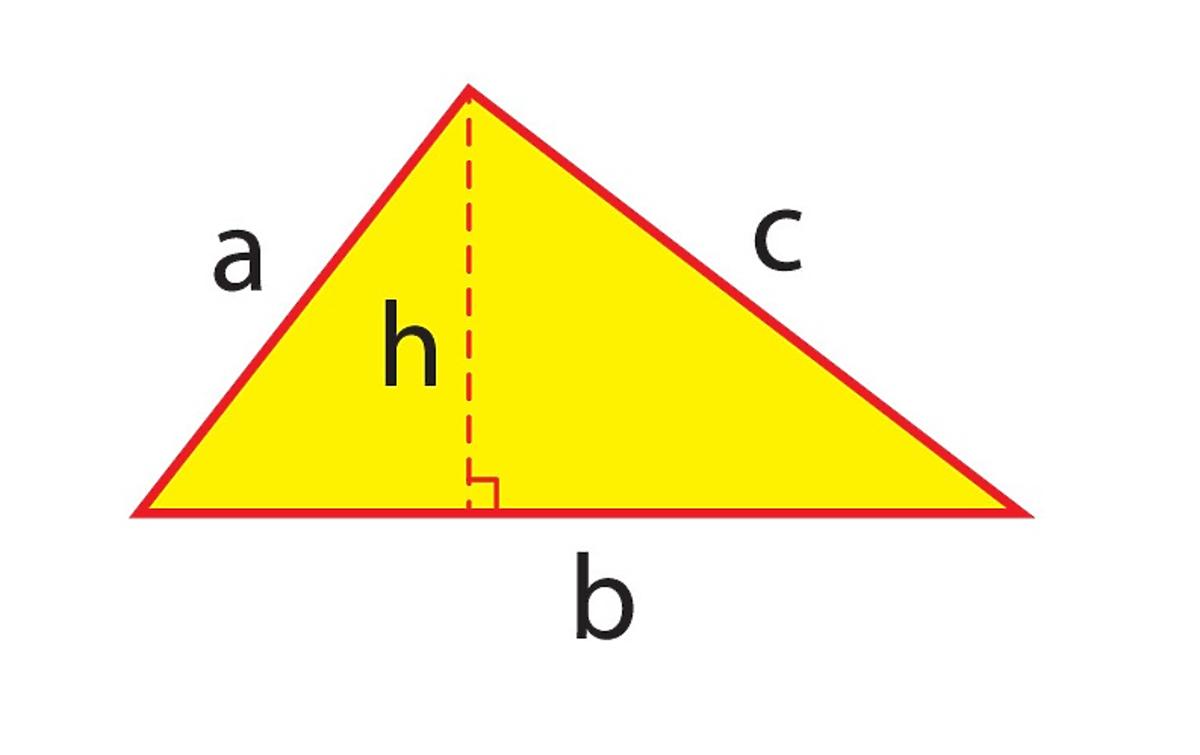
Zanim przejdziemy do wzoru na pole, warto przypomnieć sobie kilka podstawowych definicji. W trójkącie prostokątnym boki przylegające do kąta prostego nazywamy przyprostokątnymi, a bok leżący naprzeciw kąta prostego nazywamy przeciwprostokątną. Przeciwprostokątna jest zawsze najdłuższym bokiem w trójkącie prostokątnym.

Twierdzenie Pitagorasa jest fundamentalną zasadą, która opisuje związek między długościami boków w trójkącie prostokątnym: a² + b² = c², gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. Twierdzenie to jest niezwykle przydatne, ponieważ pozwala na obliczenie długości jednego boku, jeśli znamy długości dwóch pozostałych.

Oprócz twierdzenia Pitagorasa, ważne są również funkcje trygonometryczne (sinus, cosinus, tangens), które pozwalają na obliczanie długości boków i miar kątów w trójkącie prostokątnym, mając dane inne długości lub kąty.

Wzór na pole trójkąta prostokątnego

Pole trójkąta prostokątnego można obliczyć na kilka sposobów, ale najprostszy i najczęściej używany wzór wykorzystuje długości przyprostokątnych.

Wzór:

P = (1/2) * a * b

Gdzie:

P – oznacza pole trójkąta prostokątnego
a – oznacza długość jednej przyprostokątnej
b – oznacza długość drugiej przyprostokątnej

Wzór ten wynika bezpośrednio z faktu, że trójkąt prostokątny stanowi połowę prostokąta o bokach długości a i b. Pole takiego prostokąta wynosi a * b, a pole trójkąta prostokątnego, będącego jego połową, to (1/2) * a * b.

Wyjaśnienie i przykłady

Przykład 1: Załóżmy, że mamy trójkąt prostokątny, którego przyprostokątne mają długości a = 5 cm i b = 8 cm. Aby obliczyć jego pole, podstawiamy te wartości do wzoru:

P = (1/2) * 5 cm * 8 cm = 20 cm²

Zatem pole tego trójkąta prostokątnego wynosi 20 centymetrów kwadratowych.

Przykład 2: Rozważmy trójkąt prostokątny, którego jedna przyprostokątna ma długość a = 12 m, a pole wynosi P = 42 m². Chcemy obliczyć długość drugiej przyprostokątnej (b).

Przekształcamy wzór na pole:

b = (2 * P) / a

Podstawiamy wartości:

b = (2 * 42 m²) / 12 m = 7 m

Długość drugiej przyprostokątnej wynosi 7 metrów.

Alternatywne sposoby obliczania pola

Chociaż wzór P = (1/2) * a * b jest najprostszy, istnieją sytuacje, w których nie znamy długości obu przyprostokątnych. W takich przypadkach możemy wykorzystać inne metody:

Znając długość przeciwprostokątnej i jednej przyprostokątnej: Możemy użyć twierdzenia Pitagorasa do obliczenia długości drugiej przyprostokątnej, a następnie zastosować podstawowy wzór na pole.
Znając długość jednego boku i miarę jednego kąta ostrego: Możemy wykorzystać funkcje trygonometryczne (sinus, cosinus, tangens) do obliczenia długości drugiej przyprostokątnej, a następnie zastosować podstawowy wzór na pole. Na przykład, jeśli znamy długość przyprostokątnej a i kąt ostry α, możemy obliczyć długość drugiej przyprostokątnej b jako b = a * tan(α).
Używając wzoru Herona dla dowolnego trójkąta: Wzór Herona pozwala na obliczenie pola dowolnego trójkąta (w tym prostokątnego), znając długości wszystkich trzech boków. Wzór Herona jest bardziej skomplikowany, ale przydatny, gdy nie możemy bezpośrednio zastosować wzoru P = (1/2) * a * b.

Zastosowania trójkątów prostokątnych i obliczania ich pola

Trójkąty prostokątne i umiejętność obliczania ich pola mają szerokie zastosowanie w różnych dziedzinach:

Architektura i budownictwo: Projektowanie budynków, obliczanie powierzchni dachów, wyznaczanie kątów prostych podczas wznoszenia konstrukcji.
Inżynieria: Projektowanie mostów, dróg, konstrukcji stalowych, gdzie obliczenia związane z trójkątami prostokątnymi są kluczowe dla zapewnienia stabilności i bezpieczeństwa.
Nawigacja: Wyznaczanie pozycji, obliczanie odległości i kierunków, wykorzystanie trygonometrii do nawigacji morskiej i lotniczej.
Geodezja: Pomiar powierzchni terenu, tworzenie map, wyznaczanie współrzędnych.
Fizyka: Analiza ruchu, rozkład sił na składowe, obliczenia w optyce i akustyce.
Grafika komputerowa i gry wideo: Obliczenia związane z pozycjonowaniem obiektów, rzutowaniem perspektywicznym, modelowaniem 3D.
Codzienne życie: Obliczanie powierzchni podłogi podczas remontu, wyznaczanie kątów prostych podczas układania płytek, szacowanie wysokości drzewa na podstawie cienia.

Real-world examples and data

W budownictwie, podczas projektowania dachu dwuspadowego, trójkąt prostokątny powstaje na przekroju dachu. Znając szerokość budynku (podstawa trójkąta) i kąt nachylenia dachu, można obliczyć wysokość dachu (druga przyprostokątna) oraz długość krokwi (przeciwprostokątna). Następnie, można obliczyć pole powierzchni dachu, co jest niezbędne do oszacowania kosztów materiałów budowlanych.

W geodezji, pomiar powierzchni działki, która ma kształt zbliżony do trójkąta, często opiera się na podziale działki na mniejsze trójkąty, w tym trójkąty prostokątne. Dzięki temu można precyzyjnie obliczyć powierzchnię działki, nawet jeśli jej kształt nie jest idealnie regularny.

W grafice komputerowej, trójkąty (w tym prostokątne) są podstawowym elementem reprezentacji obiektów 3D. Każdy obiekt 3D jest modelowany jako siatka złożona z trójkątów. Obliczenia związane z trójkątami, takie jak obliczanie normalnych do powierzchni trójkąta (wektor prostopadły do powierzchni), są kluczowe dla poprawnego oświetlenia i renderingu sceny.

Podsumowanie

Trójkąt prostokątny to jedna z fundamentalnych figur geometrycznych, której właściwości i zastosowania są niezwykle szerokie. Wzór na pole trójkąta prostokątnego, P = (1/2) * a * b, jest prosty w użyciu i pozwala na szybkie obliczenie pola, gdy znamy długości przyprostokątnych. W sytuacjach, gdy nie znamy obu przyprostokątnych, możemy wykorzystać twierdzenie Pitagorasa, funkcje trygonometryczne lub wzór Herona, aby obliczyć pole.

Umiejętność obliczania pola trójkąta prostokątnego jest nie tylko ważna w matematyce i geometrii, ale również przydatna w wielu dziedzinach nauki, inżynierii i życia codziennego.

Ćwiczenie czyni mistrza! Zachęcam do rozwiązywania różnych zadań i przykładów, aby utrwalić wiedzę na temat obliczania pola trójkąta prostokątnego i jego zastosowań. Rozważ różne scenariusze, w których brakuje Ci jednej danej, i spróbuj ją wyliczyć za pomocą twierdzenia Pitagorasa lub funkcji trygonometrycznych. Im więcej będziesz ćwiczyć, tym lepiej zrozumiesz właściwości i zastosowania trójkątów prostokątnych.