Trojkat Prostokatny Katy 30 60 90

Czy zastanawiałeś się kiedyś, jak to możliwe, że niektóre problemy geometryczne wydają się łatwiejsze do rozwiązania niż inne? Otóż, istnieje pewien trójkąt, który kryje w sobie niezwykłe właściwości – trójkąt prostokątny o kątach 30°, 60° i 90°. Ten artykuł jest skierowany do uczniów szkół średnich, studentów, a także wszystkich entuzjastów matematyki, którzy chcą lepiej zrozumieć ten fascynujący kształt i jego zastosowania. Razem zgłębimy jego sekrety, odkryjemy zależności między bokami i nauczymy się wykorzystywać te informacje do rozwiązywania różnorodnych zadań.

Czym jest trójkąt prostokątny o kątach 30°, 60°, 90°?

Zacznijmy od definicji. Trójkąt prostokątny to trójkąt, w którym jeden z kątów jest prosty, czyli ma miarę 90°. W przypadku trójkąta o kątach 30°, 60° i 90°, pozostałe dwa kąty ostre mają miary odpowiednio 30° i 60°. To połączenie szczególnych wartości kątów sprawia, że boki takiego trójkąta pozostają w konkretnych, łatwych do zapamiętania relacjach.

Warto zauważyć, że suma kątów w każdym trójkącie wynosi 180°. W naszym przypadku mamy: 30° + 60° + 90° = 180°. Ta zasada jest fundamentem geometrii i pomaga nam zrozumieć, dlaczego trójkąt o takich kątach jest tak wyjątkowy.

Zależności między bokami trójkąta 30°, 60°, 90°

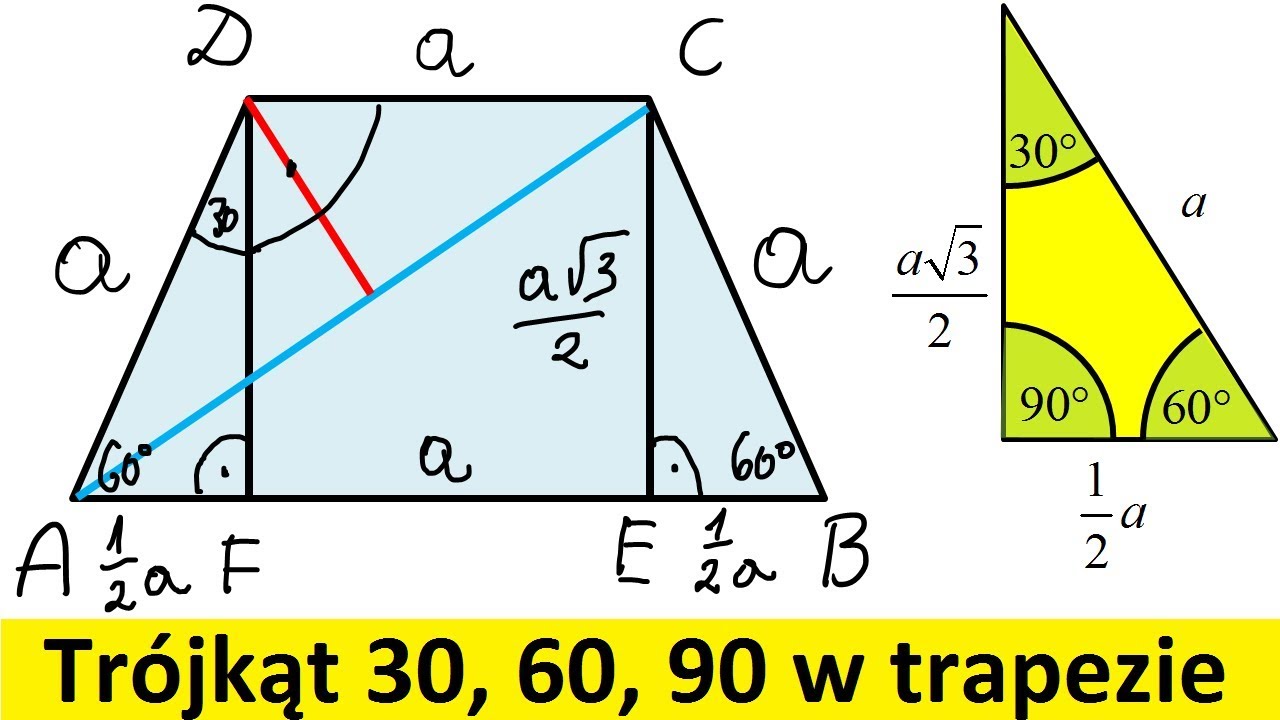
Kluczowym elementem zrozumienia trójkąta prostokątnego o kątach 30°, 60°, 90° są zależności między długościami jego boków. Te zależności wynikają z własności trójkąta równobocznego i pozwalają nam na szybkie obliczanie długości nieznanych boków, gdy znamy długość choćby jednego z nich.

Podstawowe zależności

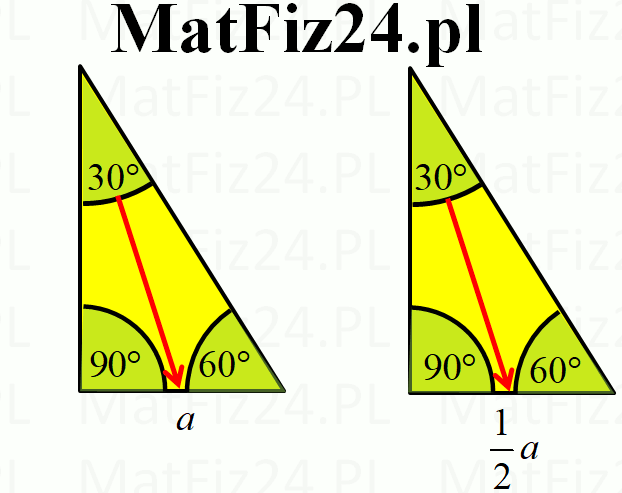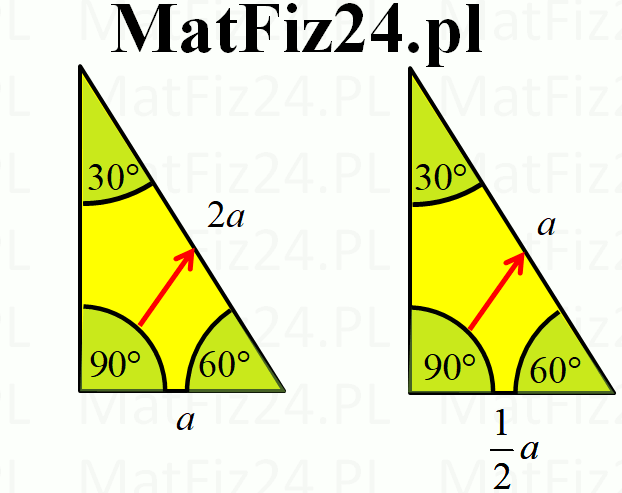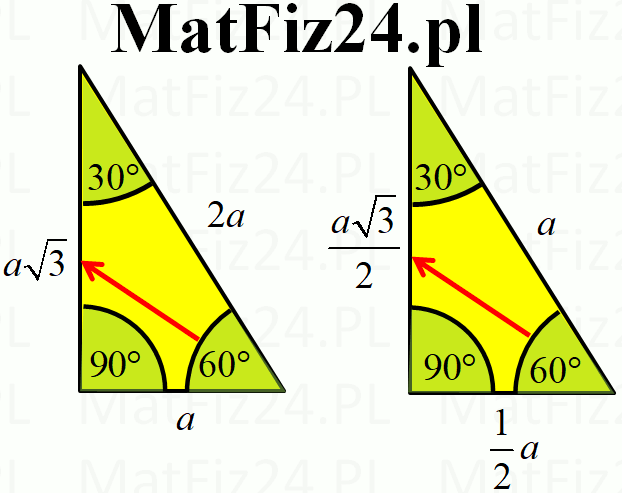
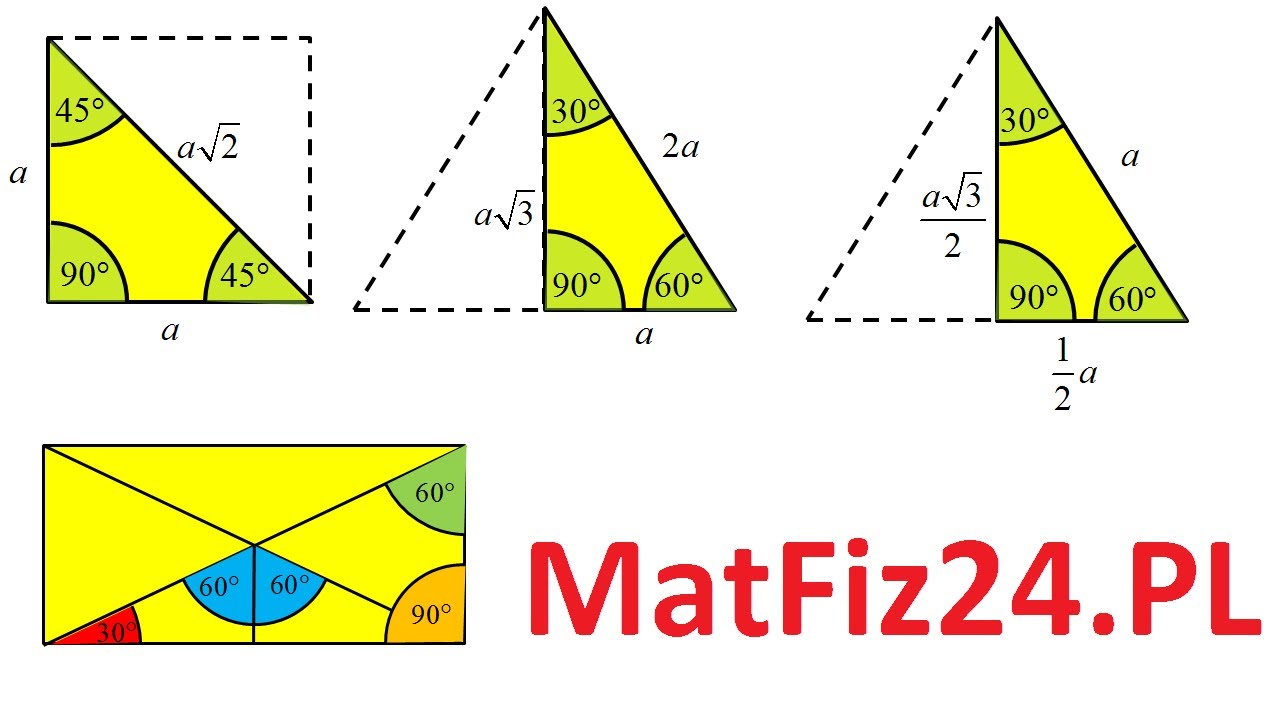
Wyobraźmy sobie trójkąt równoboczny o boku długości a. Jeśli podzielimy go na pół, prowadząc wysokość z jednego wierzchołka na przeciwległy bok, otrzymamy dwa trójkąty prostokątne o kątach 30°, 60° i 90°. Zatem:

Najkrótszy bok (naprzeciw kąta 30°) ma długość a/2 (połowa długości boku trójkąta równobocznego).
Dłuższa przyprostokątna (naprzeciw kąta 60°) ma długość (a√3)/2 (wysokość trójkąta równobocznego).
Przeciwprostokątna (naprzeciw kąta 90°) ma długość a (długość boku trójkąta równobocznego).

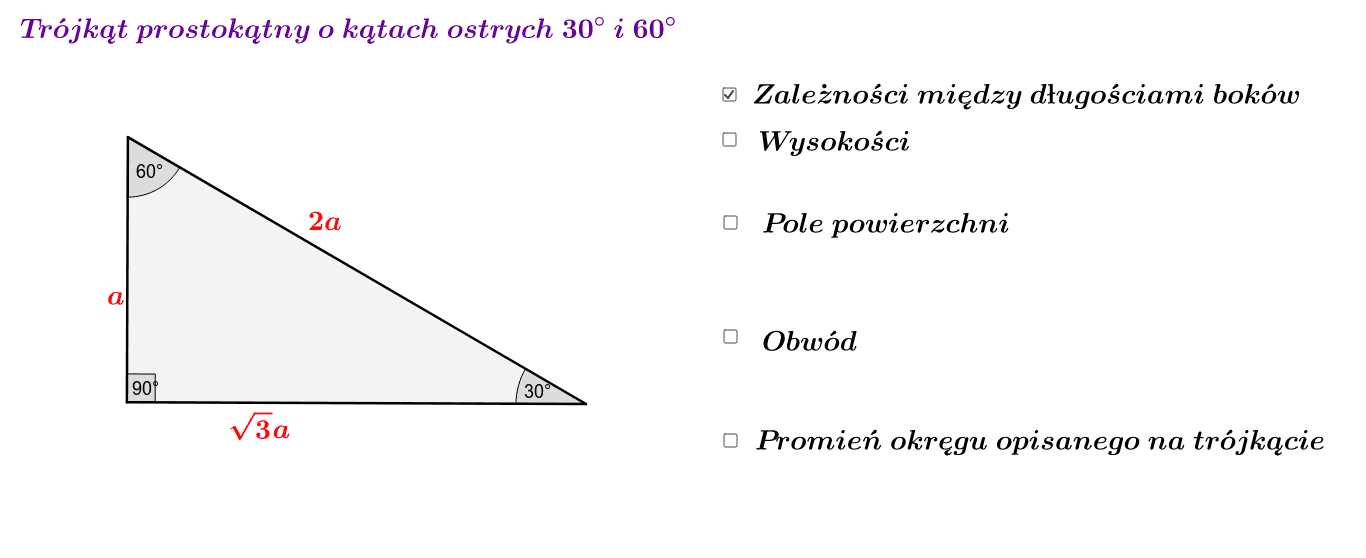
Możemy to zapisać również w następujący sposób, używając oznaczeń:

x - długość najkrótszego boku (naprzeciw kąta 30°)
x√3 - długość dłuższej przyprostokątnej (naprzeciw kąta 60°)
2x - długość przeciwprostokątnej (naprzeciw kąta 90°)

Zapamiętanie tych zależności jest kluczowe. Dzięki nim, znając długość jednego boku, możemy bez problemu obliczyć długości pozostałych.

Przykłady zastosowań

Teoria to jedno, ale praktyczne zastosowanie to zupełnie inna sprawa. Zobaczmy, jak możemy wykorzystać wiedzę o trójkącie 30°, 60°, 90° w rozwiązywaniu konkretnych zadań.

Przykład 1:

Załóżmy, że mamy trójkąt prostokątny o kątach 30°, 60°, 90°, w którym najkrótszy bok ma długość 5 cm. Jakie są długości pozostałych boków?

Rozwiązanie:

Wiemy, że najkrótszy bok (x) ma długość 5 cm.
Dłuższa przyprostokątna ma długość x√3, czyli 5√3 cm.
Przeciwprostokątna ma długość 2x, czyli 2 * 5 = 10 cm.

Odpowiedź: Dłuższa przyprostokątna ma długość 5√3 cm, a przeciwprostokątna ma długość 10 cm.

Przykład 2:

Mamy trójkąt prostokątny o kątach 30°, 60°, 90°, w którym przeciwprostokątna ma długość 12 cm. Jakie są długości pozostałych boków?

Rozwiązanie:

Wiemy, że przeciwprostokątna (2x) ma długość 12 cm.
Zatem x = 12 / 2 = 6 cm (długość najkrótszego boku).
Dłuższa przyprostokątna ma długość x√3, czyli 6√3 cm.

Odpowiedź: Najkrótszy bok ma długość 6 cm, a dłuższa przyprostokątna ma długość 6√3 cm.

Przykład 3:

Drabina o długości 8 metrów jest oparta o ścianę pod kątem 60°. Jak wysoko sięga drabina na ścianie (zakładając, że ściana jest prostopadła do podłoża)?

Rozwiązanie:

Tworzymy trójkąt prostokątny, gdzie drabina jest przeciwprostokątną (8m), a kąt między drabiną a podłożem wynosi 60°. Wysokość, na którą sięga drabina, to dłuższa przyprostokątna.
Przeciwprostokątna (2x) = 8m.
Zatem x = 8 / 2 = 4m (długość najkrótszego boku).
Wysokość (dłuższa przyprostokątna) = x√3 = 4√3 m.

Odpowiedź: Drabina sięga na wysokość 4√3 metrów na ścianie.

Jak zapamiętać zależności?

Pamiętanie zależności między bokami trójkąta 30°, 60°, 90° może wydawać się trudne na początku, ale istnieje kilka sposobów, aby to ułatwić:

Wizualizacja trójkąta równobocznego: Wyobraź sobie trójkąt równoboczny, a następnie jego połowę – trójkąt prostokątny 30°, 60°, 90°. Pamiętaj, że najkrótszy bok jest połową boku trójkąta równobocznego, a dłuższa przyprostokątna to wysokość trójkąta równobocznego.
Powtarzanie: Regularnie powtarzaj zależności między bokami, aż staną się automatyczne.
Rozwiązywanie zadań: Im więcej zadań rozwiążesz, tym lepiej utrwalisz sobie te zależności.
Tworzenie skojarzeń: Znajdź sposób, aby skojarzyć kąty i boki z łatwo zapamiętywalnymi elementami.

Gdzie jeszcze spotkasz trójkąt 30°, 60°, 90°?

Trójkąt prostokątny o kątach 30°, 60°, 90° pojawia się w wielu dziedzinach nauki i życia codziennego:

Architektura i budownictwo: Przy projektowaniu budynków, dachów, schodów.
Inżynieria: Przy obliczaniu sił, momentów i konstrukcji.
Fizyka: Przy analizie rzutów ukośnych i ruchu po okręgu.
Nawigacja: Przy wyznaczaniu kursów i odległości.
Grafika komputerowa i gry: Przy tworzeniu trójwymiarowych modeli i animacji.

Podsumowanie

Trójkąt prostokątny o kątach 30°, 60°, 90° to niezwykle ważny i często spotykany kształt w matematyce i jej zastosowaniach. Zrozumienie zależności między jego bokami pozwala na szybkie i efektywne rozwiązywanie wielu problemów geometrycznych. Mam nadzieję, że dzięki temu artykułowi, zdobyłeś/zdobyłaś solidną wiedzę na temat tego trójkąta i będziesz mógł/mogła wykorzystać ją w praktyce. Pamiętaj, że kluczem do sukcesu jest praktyka i regularne powtarzanie. Powodzenia w dalszej nauce!

Pamiętaj, że opanowanie tych zależności to inwestycja w Twoją matematyczną przyszłość. Powodzenia!