Trójkąt Prostokątny 30 60 90

Zmagasz się z trygonometrią? Czujesz, że kąty 30, 60 i 90 stopni to jakaś czarna magia? Nie jesteś sam! Wielu uczniów i studentów ma trudności z opanowaniem zasad dotyczących trójkąta prostokątnego 30-60-90. Ale mam dobrą wiadomość: to wcale nie musi być trudne! W tym artykule pokażemy Ci, jak zrozumieć ten specjalny trójkąt i wykorzystać jego właściwości w praktycznych zastosowaniach.

Czym jest Trójkąt Prostokątny 30-60-90?

Trójkąt prostokątny 30-60-90 to szczególny rodzaj trójkąta prostokątnego, którego kąty wewnętrzne mają miary odpowiednio 30 stopni, 60 stopni i 90 stopni. To, co czyni go wyjątkowym, to **ściśle określone proporcje między długościami jego boków**. Zrozumienie tych proporcji pozwala szybko rozwiązywać zadania geometryczne i trygonometryczne bez potrzeby używania kalkulatora.

Proporcje Boków: Klucz do Sukcesu

Kluczem do zrozumienia trójkąta prostokątnego 30-60-90 jest poznanie proporcji między jego bokami. Zazwyczaj te proporcje przedstawia się następująco:

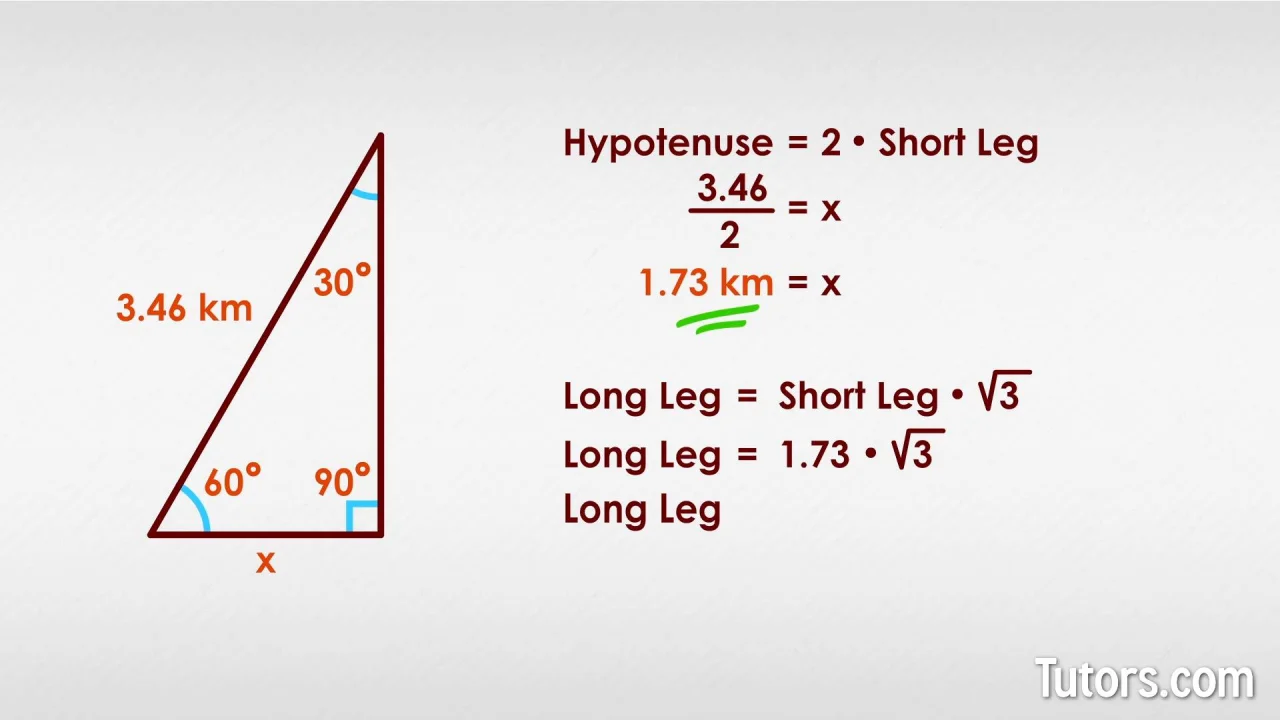
Najkrótszy bok (naprzeciw kąta 30 stopni): Oznaczmy go jako a.
Dłuższa przyprostokątna (naprzeciw kąta 60 stopni): Jej długość wynosi a√3.
Przeciwprostokątna (naprzeciw kąta 90 stopni): Jej długość wynosi 2a.

Innymi słowy: jeśli znasz długość najkrótszego boku, możesz łatwo obliczyć długości pozostałych boków, mnożąc ją odpowiednio przez √3 lub 2.

Przykład: Jeśli najkrótszy bok ma długość 5, to dłuższa przyprostokątna ma długość 5√3, a przeciwprostokątna ma długość 10.

Dlaczego Te Proporcje Działają?

Skąd w ogóle biorą się te proporcje? Można je wyprowadzić z własności trójkąta równobocznego. Wyobraźmy sobie trójkąt równoboczny o boku 2a. Jeśli podzielimy go na pół, rysując wysokość z jednego wierzchołka na przeciwległy bok, otrzymamy dwa trójkąty prostokątne 30-60-90.

Wysokość trójkąta równobocznego dzieli jego podstawę na połowy, więc najkrótszy bok naszego trójkąta prostokątnego (naprzeciw kąta 30 stopni) ma długość a. Przeciwprostokątna (która jest jednocześnie bokiem trójkąta równobocznego) ma długość 2a. Długość dłuższej przyprostokątnej (naprzeciw kąta 60 stopni) możemy obliczyć, stosując twierdzenie Pitagorasa:

(a)² + (dłuższa przyprostokątna)² = (2a)²

(dłuższa przyprostokątna)² = 4a² - a² = 3a²

dłuższa przyprostokątna = √(3a²) = a√3

W ten sposób udowodniliśmy, że proporcje boków w trójkącie prostokątnym 30-60-90 wynoszą a : a√3 : 2a.

Praktyczne Zastosowania Trójkąta 30-60-90

Trójkąt prostokątny 30-60-90 ma szerokie zastosowanie w różnych dziedzinach, od matematyki i fizyki po inżynierię i architekturę. Oto kilka przykładów:

Trygonometria: Trójkąt 30-60-90 pozwala łatwo obliczyć wartości funkcji trygonometrycznych dla kątów 30 i 60 stopni (sinus, cosinus, tangens, cotangens). Znajomość tych wartości jest kluczowa w wielu zadaniach związanych z kątami i odległościami.
Geometria: Rozwiązywanie zadań dotyczących pól i obwodów figur geometrycznych, takich jak sześciokąty foremne (które można podzielić na trójkąty równoboczne, a te z kolei na trójkąty 30-60-90) staje się znacznie prostsze.
Fizyka: Obliczanie składowych wektorów sił, prędkości i przyspieszenia w problemach związanych z ruchem po równi pochyłej lub rzutami ukośnymi.
Inżynieria i Architektura: Projektowanie konstrukcji, obliczanie kątów nachylenia dachów, wyznaczanie długości elementów konstrukcyjnych.

Przykładowe Zadania i Rozwiązania

Aby lepiej zrozumieć zastosowanie trójkąta 30-60-90, przeanalizujmy kilka przykładów:

Zadanie 1: Oblicz pole trójkąta równobocznego o boku długości 6.

Rozwiązanie: Wysokość trójkąta równobocznego dzieli go na dwa trójkąty prostokątne 30-60-90. Najkrótszy bok każdego z tych trójkątów ma długość 3 (połowa boku trójkąta równobocznego). Dłuższa przyprostokątna (wysokość trójkąta równobocznego) ma długość 3√3. Pole trójkąta równobocznego wynosi (podstawa * wysokość) / 2 = (6 * 3√3) / 2 = 9√3.

Zadanie 2: Drabina o długości 8 metrów jest oparta o ścianę, tworząc z nią kąt 60 stopni. Na jakiej wysokości sięga drabina ściany?

Rozwiązanie: Drabina, ściana i ziemia tworzą trójkąt prostokątny. Drabina to przeciwprostokątna o długości 8 metrów. Kąt między drabiną a ścianą wynosi 60 stopni, więc kąt między drabiną a ziemią wynosi 30 stopni. Wysokość, na jakiej sięga drabina ściany, to dłuższa przyprostokątna tego trójkąta. Skoro przeciwprostokątna ma długość 8 (2a), to a = 4. Dłuższa przyprostokątna (a√3) ma długość 4√3 metra.

Wskazówki i Triki

Oto kilka wskazówek, które pomogą Ci zapamiętać i efektywnie wykorzystywać właściwości trójkąta prostokątnego 30-60-90:

Zapamiętaj proporcje: Najważniejsze to zapamiętać, że stosunek długości boków wynosi a : a√3 : 2a.
Zidentyfikuj najkrótszy bok: Znalezienie najkrótszego boku jest kluczem do rozwiązania większości zadań.
Wykorzystuj twierdzenie Pitagorasa: Jeśli znasz długości dwóch boków, możesz obliczyć długość trzeciego, stosując twierdzenie Pitagorasa.
Rysuj diagramy: Rysowanie diagramów pomaga wizualizować problem i zidentyfikować trójkąty 30-60-90.
Ćwicz regularnie: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz i zapamiętasz właściwości tego trójkąta.

Pamiętaj: Ćwiczenie czyni mistrza! Nie zrażaj się początkowymi trudnościami. Regularne rozwiązywanie zadań z wykorzystaniem trójkąta prostokątnego 30-60-90 sprawi, że staniesz się w tym coraz lepszy. Wykorzystaj wiedzę z tego artykułu i przekonaj się, że trygonometria wcale nie musi być taka straszna!

Gdzie Szukać Więcej Informacji?

Jeśli chcesz pogłębić swoją wiedzę na temat trójkąta prostokątnego 30-60-90, możesz skorzystać z następujących źródeł:

Podręczniki do matematyki: Większość podręczników do geometrii i trygonometrii zawiera rozdziały poświęcone trójkątom prostokątnym, w tym trójkątom 30-60-90.
Strony internetowe i kanały na YouTube: Istnieje wiele stron internetowych i kanałów na YouTube, które oferują darmowe materiały edukacyjne, w tym lekcje wideo i ćwiczenia z rozwiązaniami. Szukaj haseł takich jak "trójkąt 30 60 90", "specjalne trójkąty prostokątne" lub "trigonometry basics".
Kursy online: Platformy edukacyjne oferują wiele kursów online z matematyki, w tym kursy poświęcone geometrii i trygonometrii.

Podsumowując, trójkąt prostokątny 30-60-90 to potężne narzędzie, które ułatwia rozwiązywanie wielu problemów geometrycznych i trygonometrycznych. Zrozumienie proporcji jego boków i regularne ćwiczenia pozwolą Ci opanować tę wiedzę i wykorzystać ją w praktyce. Powodzenia!