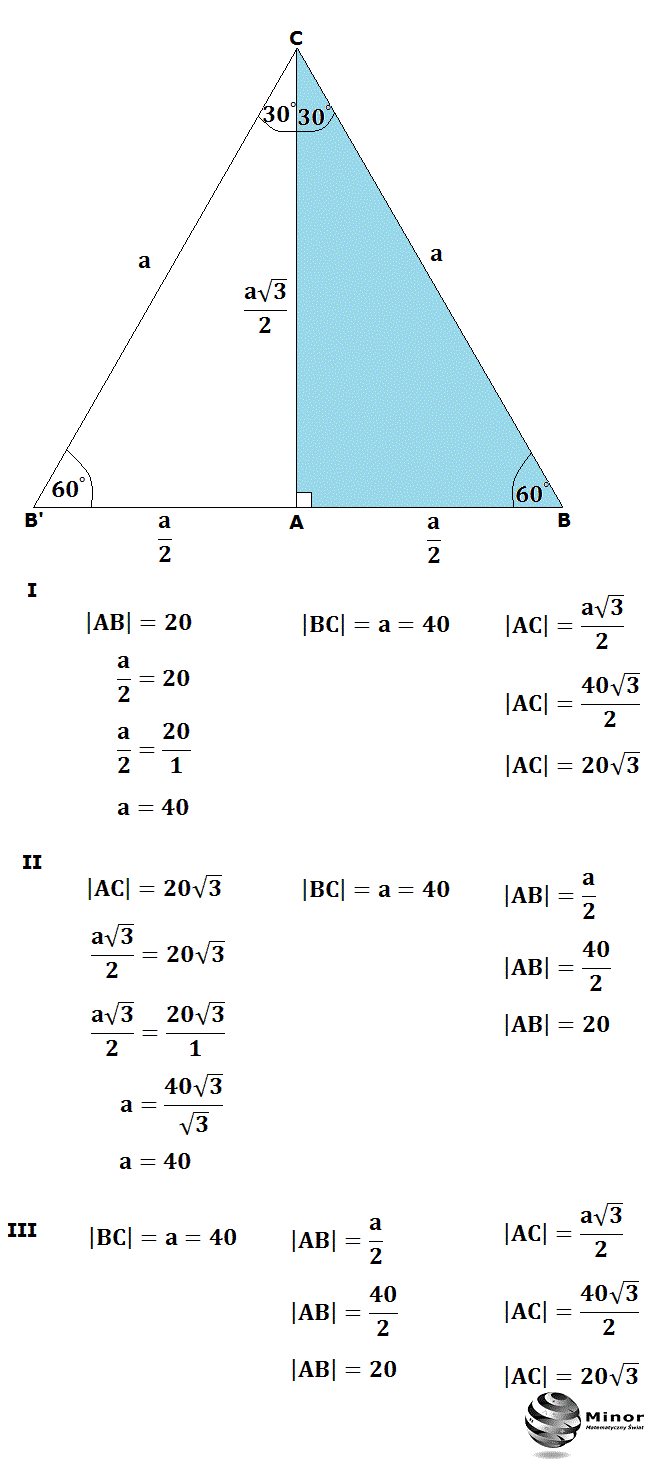Trojkat O Katach 60 30 90

Czy kiedykolwiek zastanawiałeś się, jak matematyka pomaga nam projektować budynki, obliczać odległości, a nawet rozumieć ruch gwiazd? Kluczem do wielu z tych zastosowań jest geometria, a szczególnie jeden niezwykły trójkąt: trójkąt o kątach 60, 30 i 90 stopni. Ten artykuł jest skierowany do wszystkich, którzy chcą lepiej zrozumieć ten fascynujący kształt, niezależnie od tego, czy jesteś uczniem, studentem, czy po prostu osobą ciekawą świata matematyki. Razem odkryjemy jego właściwości, zastosowania i pokażemy, dlaczego warto go znać.

Wprowadzenie do trójkąta 60-30-90

Trójkąt o kątach 60, 30 i 90 stopni to szczególny rodzaj trójkąta prostokątnego. Co go wyróżnia? Przede wszystkim to, że jego kąty mają ustalone miary: 60 stopni, 30 stopni i oczywiście 90 stopni. To sprawia, że ma on unikalne właściwości, które ułatwiają rozwiązywanie wielu problemów geometrycznych. Zrozumienie tych właściwości jest kluczowe do efektywnego korzystania z niego w praktyce.

Czym jest trójkąt prostokątny?

• Trójkąt prostokątny to trójkąt, w którym jeden z kątów jest kątem prostym, czyli ma miarę 90 stopni.
• Dwa pozostałe kąty są ostre (mniejsze niż 90 stopni).
• Bok leżący naprzeciwko kąta prostego nazywamy przeciwprostokątną, a pozostałe dwa boki to przyprostokątne.

W przypadku trójkąta 60-30-90, to właśnie kąt 90 stopni daje nam pewność, że mamy do czynienia z trójkątem prostokątnym. Dwa pozostałe kąty (60 i 30 stopni) dodają mu specyficznych cech, które omówimy w dalszej części artykułu.

Właściwości trójkąta 60-30-90

Najważniejszą cechą trójkąta 60-30-90 jest relacja między długościami jego boków. Ta relacja jest stała i wynika z jego specyficznych kątów. Zrozumienie tej relacji pozwala nam na obliczanie długości boków, mając podaną długość tylko jednego z nich!

Zależności między bokami

Oto kluczowe zależności, które musisz zapamiętać:

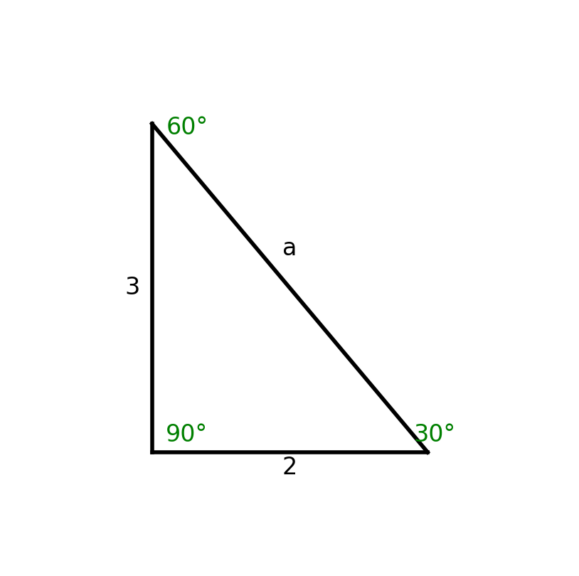
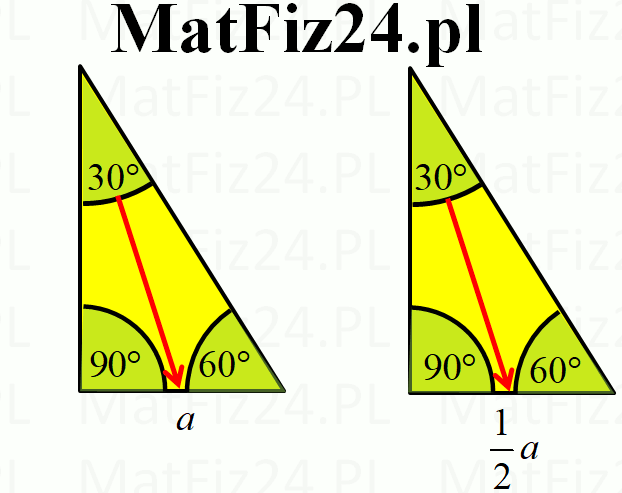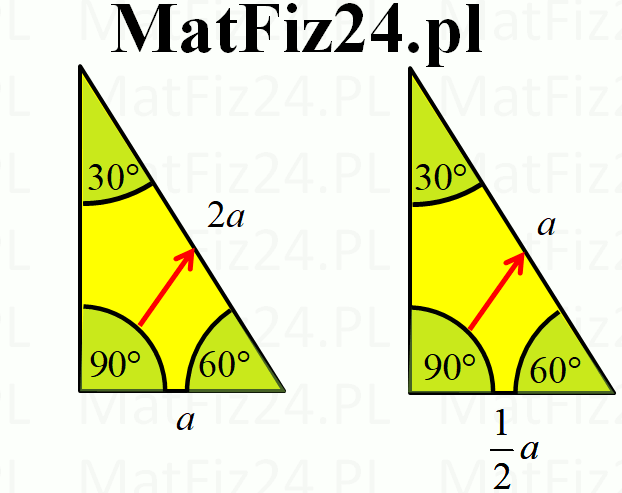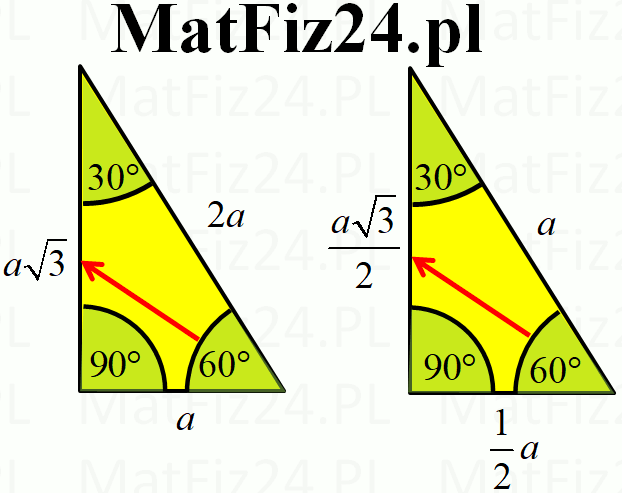
• Bok naprzeciwko kąta 30 stopni (krótsza przyprostokątna): Oznaczmy jego długość jako a.
• Bok naprzeciwko kąta 60 stopni (dłuższa przyprostokątna): Jego długość wynosi a√3.
• Przeciwprostokątna: Jej długość wynosi 2a.

Czyli, mając bok naprzeciwko kąta 30 stopni, możemy łatwo obliczyć pozostałe boki mnożąc go przez √3 (aby otrzymać dłuższą przyprostokątną) lub przez 2 (aby otrzymać przeciwprostokątną). Analogicznie, znając długość przeciwprostokątnej, możemy podzielić ją przez 2, aby otrzymać długość krótszej przyprostokątnej, a następnie pomnożyć wynik przez √3, aby otrzymać długość dłuższej przyprostokątnej.

Dowód zależności

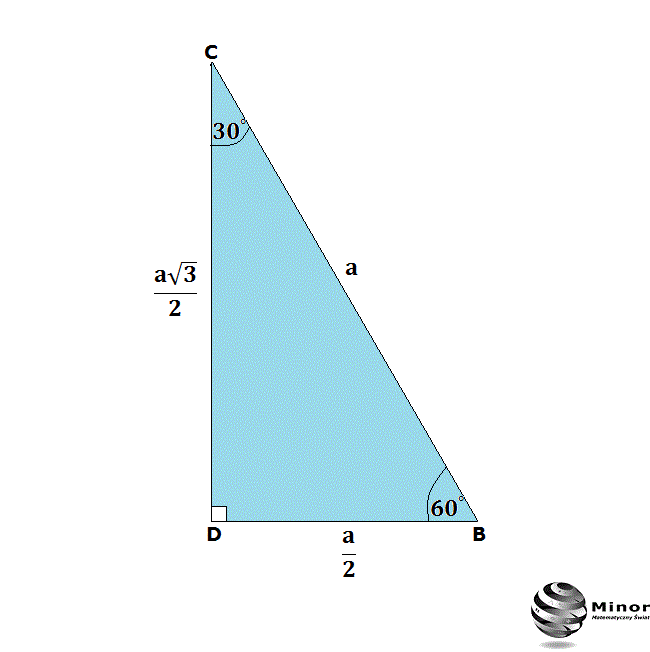
Skąd biorą się te zależności? Możemy je wyprowadzić rozważając trójkąt równoboczny. Podzielmy trójkąt równoboczny na dwie równe części, prowadząc wysokość z jednego wierzchołka na przeciwległy bok. W ten sposób otrzymamy dwa trójkąty prostokątne o kątach 30, 60 i 90 stopni. Długość boku trójkąta równobocznego staje się długością przeciwprostokątnej w naszym trójkącie 60-30-90. Wysokość trójkąta równobocznego staje się dłuższą przyprostokątną, a połowa boku trójkąta równobocznego staje się krótszą przyprostokątną. Stosując twierdzenie Pitagorasa do jednego z trójkątów 60-30-90, możemy potwierdzić powyższe zależności.

Zastosowania trójkąta 60-30-90

Trójkąt 60-30-90 ma szerokie zastosowanie w różnych dziedzinach. Oto kilka przykładów:

Trygonometria

W trygonometrii, trójkąt 60-30-90 jest bardzo przydatny do obliczania wartości funkcji trygonometrycznych dla kątów 30 i 60 stopni. Na przykład:

• sin(30°) = 1/2
• cos(30°) = √3/2
• tan(30°) = √3/3
• sin(60°) = √3/2
• cos(60°) = 1/2
• tan(60°) = √3

Znając te wartości, możemy rozwiązywać zadania związane z obliczaniem wysokości budynków, odległości do niedostępnych obiektów, czy kątów w różnych konstrukcjach.

Geometria

W geometrii, trójkąt 60-30-90 pomaga w obliczaniu pól i obwodów figur geometrycznych, które zawierają elementy trójkątne. Na przykład, możemy go użyć do obliczenia pola sześciokąta foremnego (który można podzielić na sześć trójkątów równobocznych, a każdy z nich z kolei na dwa trójkąty 60-30-90), rombu, czy trapezu.

Fizyka

W fizyce, trójkąt 60-30-90 znajduje zastosowanie w analizie wektorów, na przykład przy rozkładaniu sił na składowe. Pozwala to na łatwiejsze obliczanie wypadkowej siły działającej na ciało, czy analizę ruchu po równi pochyłej.

Architektura i Inżynieria

Architekci i inżynierowie wykorzystują trójkąty 60-30-90 w projektowaniu budynków, mostów i innych konstrukcji. Pozwalają one na precyzyjne obliczenia i zapewniają stabilność i wytrzymałość konstrukcji. Przykładowo, kąty nachylenia dachów często wykorzystują proporcje wynikające z tego trójkąta.

Przykładowe zadania

Aby lepiej zrozumieć, jak wykorzystać wiedzę o trójkącie 60-30-90 w praktyce, rozwiążmy kilka przykładowych zadań:

1. Zadanie 1: Krótsza przyprostokątna trójkąta 60-30-90 ma długość 5 cm. Oblicz długość pozostałych boków.
• Rozwiązanie:
  • Dłuższa przyprostokątna: 5√3 cm
  • Przeciwprostokątna: 2 * 5 = 10 cm
2. Zadanie 2: Przeciwprostokątna trójkąta 60-30-90 ma długość 12 cm. Oblicz długość pozostałych boków.
• Rozwiązanie:
  • Krótsza przyprostokątna: 12 / 2 = 6 cm
  • Dłuższa przyprostokątna: 6√3 cm
3. Zadanie 3: Dłuższa przyprostokątna trójkąta 60-30-90 ma długość 8√3 cm. Oblicz długość pozostałych boków.
• Rozwiązanie:
  • Krótsza przyprostokątna: 8√3 / √3 = 8 cm
  • Przeciwprostokątna: 2 * 8 = 16 cm

Wskazówki i triki

Oto kilka wskazówek, które pomogą Ci w rozwiązywaniu zadań z trójkątem 60-30-90:

• Zapamiętaj wzory: Najważniejsze to zapamiętać zależności między bokami (a, a√3, 2a).
• Zacznij od identyfikacji: Zawsze zacznij od zidentyfikowania, który bok jest dany i który musisz obliczyć.
• Upraszczaj pierwiastki: Zwróć uwagę na upraszczanie wyrażeń z pierwiastkami.
• Rysuj diagramy: Narysuj diagram trójkąta, aby lepiej wizualizować problem.
• Sprawdzaj odpowiedzi: Po obliczeniu, sprawdź, czy twoje odpowiedzi mają sens w kontekście problemu. Na przykład, przeciwprostokątna zawsze musi być najdłuższym bokiem.

Podsumowanie

Trójkąt o kątach 60, 30 i 90 stopni to niezwykle użyteczne narzędzie w matematyce, fizyce, architekturze i wielu innych dziedzinach. Jego unikalne właściwości i łatwe do zapamiętania zależności między bokami sprawiają, że jest on niezastąpiony przy rozwiązywaniu wielu problemów. Zrozumienie jego właściwości to klucz do sukcesu w wielu dziedzinach nauki i techniki. Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć ten fascynujący kształt. Zachęcamy do dalszego zgłębiania wiedzy na temat geometrii i wykorzystywania jej w praktyce. Pamiętaj, że matematyka jest wszędzie wokół nas, a trójkąt 60-30-90 jest tego doskonałym przykładem. Dzięki temu artykułowi, poszerzyłeś swoją wiedzę i zyskałeś nowe narzędzie do rozwiązywania problemów!