Trojkat Ekierkowy 30 60 90

Zmagasz się z geometrią? Masz wrażenie, że kąty i boki to tylko abstrakcyjne liczby bez związku z rzeczywistością? Wiem, jak to jest. Sam kiedyś gubiłem się w obliczeniach, dopóki nie zrozumiałem mocy jednego prostego narzędzia: trójkąta ekierkowego 30-60-90. To nie tylko kolejny przyrząd w piórniku, ale klucz do rozwiązywania wielu problemów, zarówno w szkole, jak i w życiu codziennym.

Czym właściwie jest trójkąt ekierkowy 30-60-90?

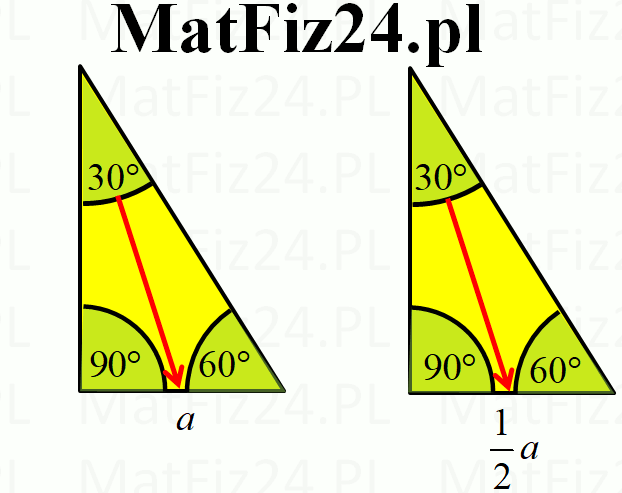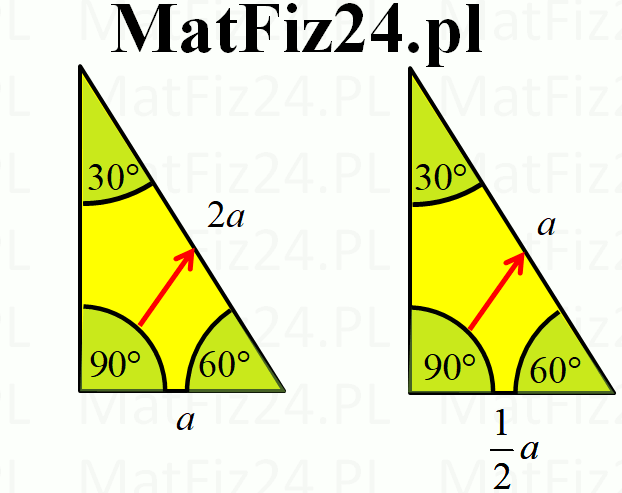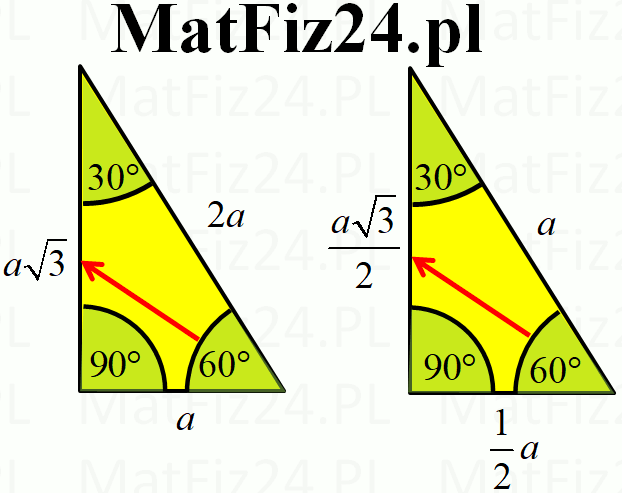
Wyobraź sobie trójkąt prostokątny, w którym jeden z kątów ostrych ma 30 stopni, a drugi 60. To właśnie on! Charakteryzuje się on specyficznymi zależnościami między długościami boków, które, jeśli raz zrozumiesz, zostaną z Tobą na zawsze.

Zależności między bokami:

Przeciwprostokątna (najdłuższy bok): Jest dwa razy dłuższa niż bok przyległy do kąta 60 stopni (czyli krótsza przyprostokątna).
Bok przyległy do kąta 30 stopni (dłuższa przyprostokątna): Jest √3 razy dłuższy niż bok przyległy do kąta 60 stopni (krótsza przyprostokątna).

Brzmi skomplikowanie? Spójrzmy na to inaczej. Jeśli krótsza przyprostokątna ma długość 'a', to:

Przeciwprostokątna ma długość '2a'
Dłuższa przyprostokątna ma długość 'a√3'

Zapamiętaj te zależności! Stanowią one fundament do rozwiązywania wielu zadań.

Gdzie wykorzystujemy trójkąt ekierkowy 30-60-90?

Może wydawać się, że to tylko szkolny temat, ale trójkąt ekierkowy ma wiele praktycznych zastosowań. Nie wierzysz? Spójrz:

Budownictwo i Architektura: Używany do obliczania wymiarów dachów, schodów, belek i innych elementów konstrukcyjnych. Znajomość kątów 30, 60 i 90 stopni jest kluczowa do projektowania stabilnych i estetycznych budynków.
Inżynieria: Wykorzystywany w obliczeniach sił, momentów i naprężeń w konstrukcjach mechanicznych. Pomaga w projektowaniu mostów, maszyn i urządzeń.
Geodezja: Stosowany w pomiarach terenowych, wyznaczaniu wysokości i odległości. Dzięki niemu możemy precyzyjnie mapować teren.
Nawigacja: Używany w obliczeniach związanych z trasami, odległościami i kierunkami. Szczególnie przydatny w żeglarstwie i lotnictwie.
Grafika komputerowa i gry wideo: Pomaga w tworzeniu trójwymiarowych modeli i animacji. Kąty i proporcje odgrywają kluczową rolę w realistycznym odwzorowaniu świata.

To tylko kilka przykładów. W rzeczywistości, trójkąt ekierkowy 30-60-90 znajduje zastosowanie wszędzie tam, gdzie mamy do czynienia z kątami i proporcjami. Pomyśl o projektowaniu mebli, układaniu płytek, a nawet o obliczaniu, jak daleko sięgnie rzut piłką!

Przykłady zastosowań i rozwiązywanie problemów

Ok, teoria to jedno, ale praktyka to drugie. Zobaczmy, jak możemy wykorzystać naszą wiedzę do rozwiązywania konkretnych zadań.

Przykład 1:

Mamy trójkąt ekierkowy 30-60-90, w którym krótsza przyprostokątna ma długość 5 cm. Oblicz długość pozostałych boków.

Rozwiązanie:

Krótsza przyprostokątna (a) = 5 cm
Przeciwprostokątna (2a) = 2 * 5 cm = 10 cm
Dłuższa przyprostokątna (a√3) = 5√3 cm ≈ 8.66 cm

Przykład 2:

Dach ma kształt trójkąta równobocznego o boku 6 metrów. Jak wysoka jest ściana szczytowa (wysokość trójkąta)?

Rozwiązanie:

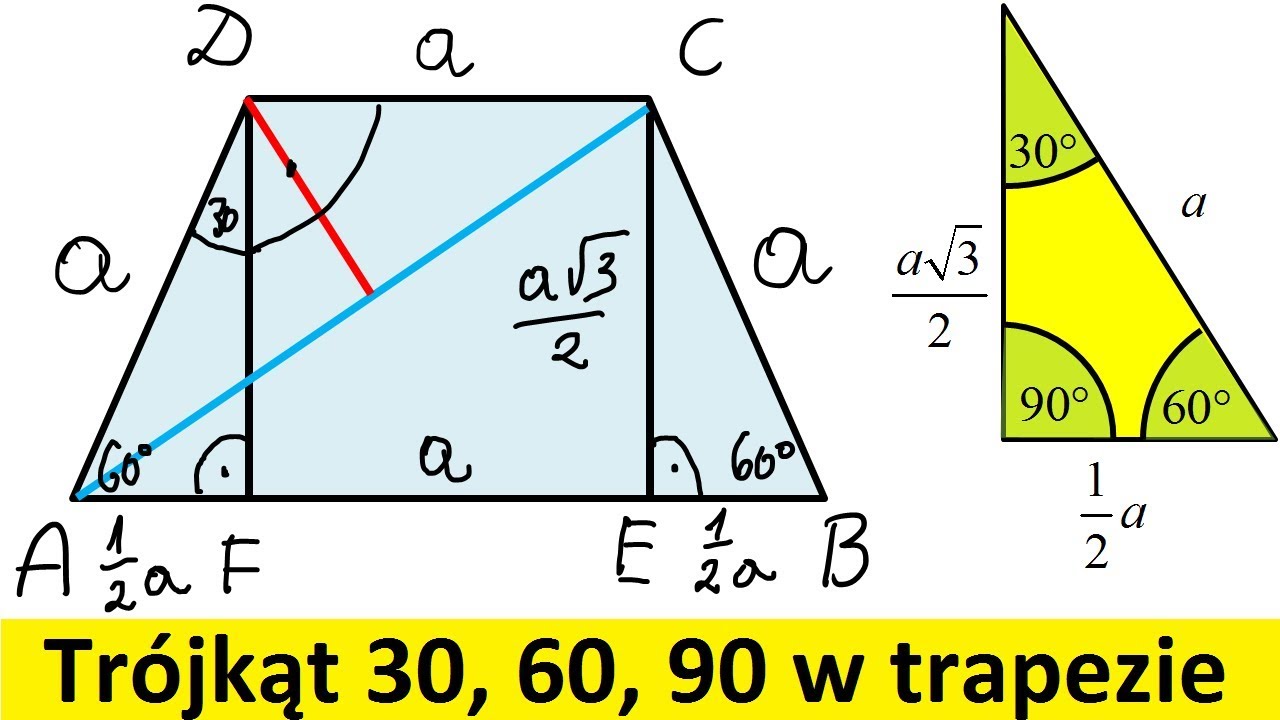
Wysokość trójkąta równobocznego dzieli go na dwa trójkąty ekierkowe 30-60-90. Bok trójkąta równobocznego staje się przeciwprostokątną trójkąta ekierkowego. Krótsza przyprostokątna to połowa boku trójkąta równobocznego (6m / 2 = 3m).

Wysokość (czyli dłuższa przyprostokątna) = 3√3 m ≈ 5.20 m

Counterpoints: Czy trójkąt ekierkowy jest zawsze potrzebny?

Oczywiście, że nie! W niektórych sytuacjach możemy użyć kalkulatora, programu komputerowego lub innych metod. Jednak znajomość zależności w trójkącie ekierkowym 30-60-90 daje nam intuicję geometryczną. Pozwala nam na szybkie oszacowanie wyników, sprawdzenie poprawności obliczeń i zrozumienie, co tak naprawdę się dzieje. To umiejętność, która przydaje się w wielu sytuacjach, nawet jeśli nie mamy pod ręką kalkulatora.

Ponadto, zrozumienie trójkąta ekierkowego jest często fundamentem do nauki trygonometrii. Bez tej podstawowej wiedzy, trudniej będzie zrozumieć bardziej zaawansowane koncepcje.

Jak skutecznie opanować wiedzę o trójkącie ekierkowym?

Ćwicz! Rozwiązuj jak najwięcej zadań. Im więcej praktyki, tym lepiej zrozumiesz zależności między bokami.
Rysuj! Rysuj trójkąty ekierkowe o różnych wymiarach. To pomoże Ci wizualizować zależności.
Szukaj przykładów w życiu codziennym! Zwróć uwagę na kąty i proporcje w otaczającym Cię świecie. Zobacz, jak trójkąt ekierkowy przejawia się w architekturze, designie i innych dziedzinach.
Korzystaj z zasobów online! Istnieje wiele stron internetowych i filmów wideo, które mogą pomóc Ci zrozumieć trójkąt ekierkowy.
Nie bój się pytać! Jeśli masz wątpliwości, zapytaj nauczyciela, kolegę lub poszukaj odpowiedzi na forach internetowych.

Podsumowanie: Trójkąt ekierkowy to Twój sojusznik!

Trójkąt ekierkowy 30-60-90 to nie tylko figura geometryczna, ale potężne narzędzie, które może pomóc Ci w rozwiązywaniu problemów w wielu dziedzinach. Znajomość zależności między jego bokami daje Ci przewagę i pozwala na szybsze i bardziej precyzyjne obliczenia. Pamiętaj, że kluczem do sukcesu jest praktyka i zrozumienie podstawowych zasad.

Zatem, co zrobisz z tą wiedzą? Jak wykorzystasz trójkąt ekierkowy 30-60-90 w swoim życiu?