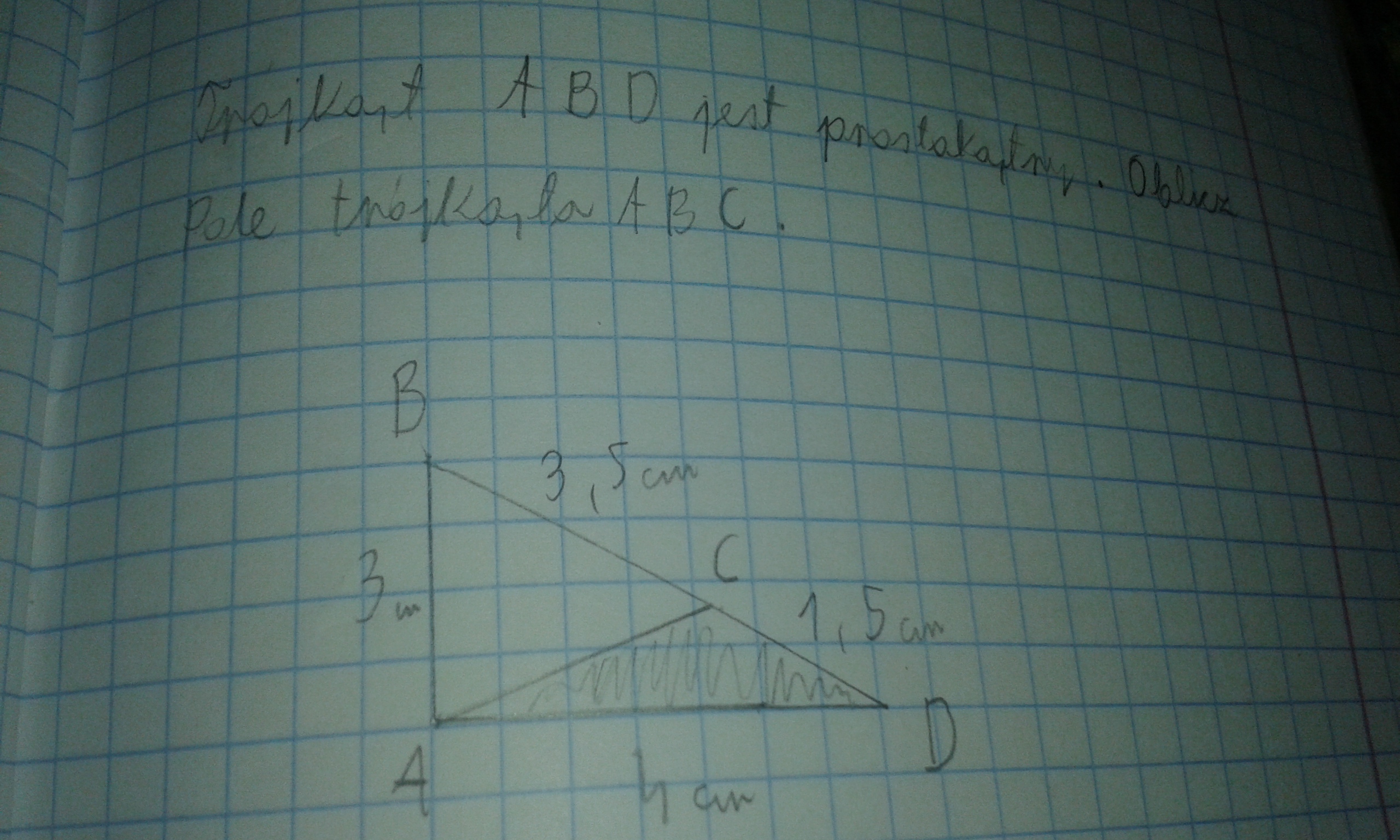
Trójkąt Abd Jest Prostokątny Oblicz Pole Trójkąta Acd

Rozważmy trójkąt ABC, gdzie kąt przy wierzchołku B jest prosty. Oznacza to, że mamy do czynienia z trójkątem prostokątnym. Znając długości boków AB i BC, możemy bez problemu obliczyć pole tego trójkąta. Kluczowe jest jednak zrozumienie, jak wykorzystać tę informację do obliczenia pola trójkąta ACD, który jest powiązany z trójkątem ABC.

Załóżmy, że bok AC trójkąta ABC jest podstawą trójkąta ACD. Aby obliczyć pole trójkąta ACD, potrzebujemy znać długość podstawy AC oraz wysokość opuszczoną na tę podstawę z wierzchołka D. Długość boku AC możemy obliczyć, korzystając z twierdzenia Pitagorasa, ponieważ trójkąt ABC jest prostokątny. Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych (AB i BC) jest równa kwadratowi długości przeciwprostokątnej (AC).

Zatem, AC² = AB² + BC². Po obliczeniu AC, czyli długości podstawy trójkąta ACD, musimy znaleźć wysokość opuszczoną na tę podstawę z wierzchołka D. Bez dodatkowych informacji, takich jak współrzędne punktu D, kąty w trójkącie ACD, czy też relacje między bokami ACD i ABC, bezpośrednie obliczenie wysokości jest niemożliwe.

Spróbujmy rozważyć kilka scenariuszy.

Scenariusz 1: Punkt D leży na prostej AB.

Jeśli punkt D leży na prostej AB, a konkretnie na odcinku AB lub jego przedłużeniu, sytuacja staje się bardziej klarowna. Załóżmy, że znamy długość AD. Wówczas, możemy obliczyć pole trójkąta ACD, mając podstawę AC (obliczoną wcześniej z twierdzenia Pitagorasa) i wysokość. Wysokość w tym przypadku będzie równa długości odcinka BC, ponieważ kąt ABC jest prosty, a BC jest prostopadła do AB.

W takim przypadku, pole trójkąta ACD możemy obliczyć jako (1/2) * AC * BC.

Scenariusz 2: Punkt D leży poza prostą AB.

Jeśli punkt D leży poza prostą AB, potrzebujemy dodatkowych informacji. Możemy na przykład znać współrzędne punktów A, C i D. Wówczas możemy użyć wzoru na pole trójkąta, wykorzystując współrzędne wierzchołków. Wzór ten brzmi:

Pole = (1/2) * |(x_A(y_C - y_D) + x_C(y_D - y_A) + x_D(y_A - y_C))|

Gdzie (x_A, y_A), (x_C, y_C) i (x_D, y_D) to współrzędne punktów A, C i D odpowiednio.

Inną możliwością jest znajomość długości boków AC, AD i CD. Wtedy możemy użyć wzoru Herona. Wzór Herona pozwala obliczyć pole trójkąta, znając długości wszystkich jego boków.

Obliczamy połowę obwodu trójkąta (s):

s = (AC + AD + CD) / 2

Następnie, pole trójkąta ACD obliczamy ze wzoru:

Pole = √(s(s - AC)(s - AD)(s - CD))

Aby móc konkretnie obliczyć pole trójkąta ACD, potrzebujemy znać albo współrzędne punktu D, albo długości boków AD i CD, albo informację o tym, jak punkt D jest powiązany z trójkątem ABC. Bez tych danych, możemy jedynie operować na ogólnych wzorach i rozważać hipotetyczne scenariusze.

Załóżmy, że znamy długości boków AB = 3 i BC = 4. Wtedy, z twierdzenia Pitagorasa, możemy obliczyć długość boku AC:

AC² = AB² + BC² = 3² + 4² = 9 + 16 = 25 AC = √25 = 5

Teraz załóżmy, że znamy współrzędne punktów: A(0, 0), B(3, 0) i C(3, 4). Punkt D ma współrzędne (0,5). Wtedy możemy obliczyć pole trójkąta ACD, korzystając ze wzoru na pole trójkąta za pomocą współrzędnych wierzchołków:

Pole = (1/2) * |(0*(4 - 5) + 3*(5 - 0) + 0*(0 - 4))| Pole = (1/2) * |(0 + 15 + 0)| Pole = (1/2) * 15 = 7.5

Zatem, pole trójkąta ACD w tym przypadku wynosi 7.5 jednostek kwadratowych.

Jeśli zamiast współrzędnych punktu D znamy długości boków AD i CD, na przykład AD = √26 i CD = √17, wtedy możemy skorzystać ze wzoru Herona.

Obliczamy połowę obwodu (s):

s = (5 + √26 + √17) / 2 ≈ (5 + 5.1 + 4.1) / 2 ≈ 7.1

Następnie, obliczamy pole trójkąta ACD:

Pole = √(7.1 * (7.1 - 5) * (7.1 - √26) * (7.1 - √17)) Pole ≈ √(7.1 * 2.1 * 2 * 3) Pole ≈ √(89.46) Pole ≈ 9.46

Zatem, w tym przypadku pole trójkąta ACD wynosi około 9.46 jednostek kwadratowych.

Ważne jest, aby pamiętać, że wybór metody obliczania pola trójkąta ACD zależy od dostępnych danych. Jeżeli mamy współrzędne, używamy wzoru ze współrzędnymi. Jeżeli mamy długości boków, używamy wzoru Herona. Jeżeli znamy tylko relacje geometryczne (np. punkt D leży na prostej AB), musimy odpowiednio dostosować podejście.

Konieczne jest precyzyjne zrozumienie zadania i wykorzystanie dostępnych informacji w najbardziej efektywny sposób. Bez jasnych danych o punkcie D, obliczenie pola trójkąta ACD jest niemożliwe. Należy zawsze analizować zadanie pod kątem dostępnych informacji i wybrać odpowiednią strategię rozwiązania.

Na zakończenie, podkreślmy raz jeszcze, że obliczenie pola trójkąta ACD wymaga konkretnych danych dotyczących punktu D. Wykorzystanie twierdzenia Pitagorasa do obliczenia długości boku AC jest kluczowe, ale to tylko pierwszy krok. Dalsze kroki zależą od tego, co wiemy o punkcie D i jego relacji z trójkątem ABC.