Trojkat 45 45 90 Wlasnosci

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre konstrukcje budowlane są tak stabilne? Albo dlaczego tak wiele przedmiotów codziennego użytku ma kształt trójkąta? Często odpowiedź leży w geometrii, a konkretnie w wyjątkowych właściwościach trójkąta prostokątnego równoramiennego, znanego również jako trójkąt 45 45 90. Rozumienie tego trójkąta może ułatwić obliczenia, projekty i codzienne zadania.

W tym artykule przyjrzymy się bliżej temu niezwykłemu kształtowi. Zobaczymy, jakie unikalne cechy posiada i jak możemy wykorzystać jego właściwości w praktyce. Niezależnie od tego, czy jesteś uczniem, studentem, inżynierem czy po prostu osobą ciekawą świata, zrozumienie trójkąta 45 45 90 z pewnością okaże się przydatne.

Czym jest Trójkąt 45 45 90?

Trójkąt 45 45 90 to trójkąt prostokątny, którego dwa kąty ostre mają miarę 45 stopni każdy. Oznacza to, że jest to również trójkąt równoramienny – dwa boki przylegające do kąta prostego są równej długości.

Wyobraź sobie kwadrat. Jeśli przetniesz go po przekątnej, otrzymasz dwa identyczne trójkąty 45 45 90. To proste, ale bardzo ważne spostrzeżenie, które pomaga zrozumieć jego właściwości.

Kluczowe Właściwości Trójkąta 45 45 90

Trójkąt 45 45 90 posiada kilka fundamentalnych właściwości, które czynią go wyjątkowym:

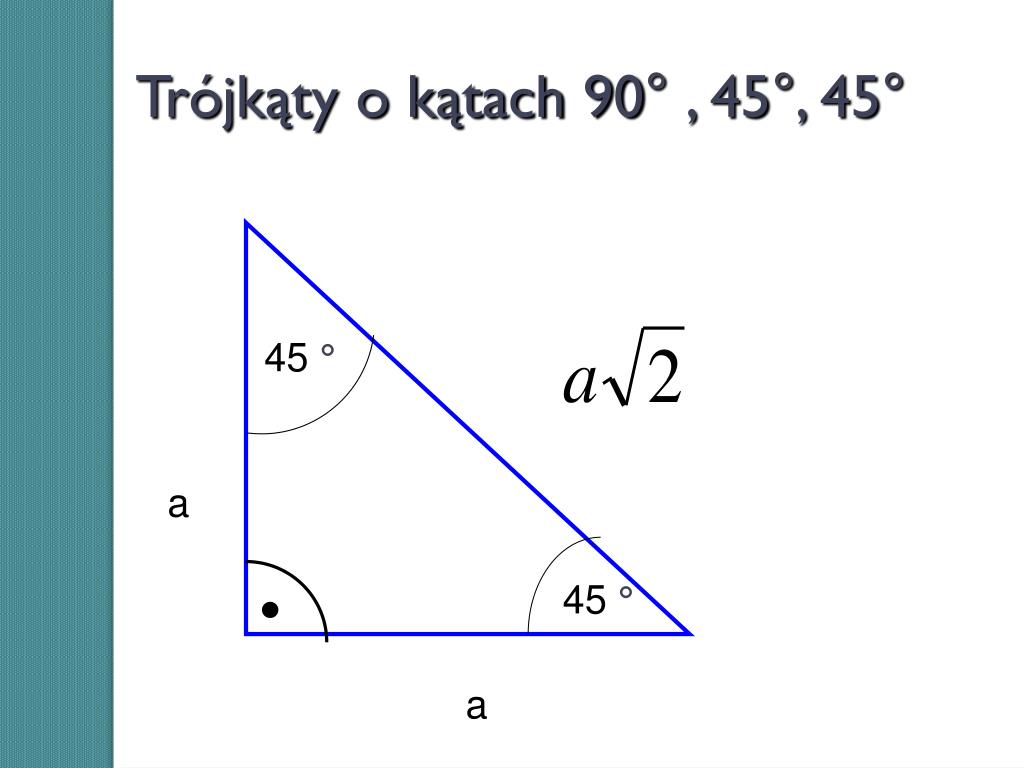
Kąty: Dwa kąty ostre mają miarę 45 stopni, a kąt prosty ma miarę 90 stopni.
Boki: Dwa boki przylegające do kąta prostego (przyprostokątne) są równej długości. Oznaczmy długość każdej z nich jako 'a'.
Przeciwprostokątna: Długość przeciwprostokątnej (bok naprzeciw kąta prostego) wynosi a√2, gdzie 'a' to długość przyprostokątnej.

Ta ostatnia właściwość jest kluczowa. Znając długość jednego boku trójkąta 45 45 90, możemy natychmiast obliczyć długości pozostałych boków. Nie potrzebujemy do tego żadnych skomplikowanych obliczeń trygonometrycznych!

Związek Między Bokami: 1 : 1 : √2

Relację między bokami trójkąta 45 45 90 można wyrazić w prosty sposób: 1 : 1 : √2. Oznacza to, że jeśli jeden bok ma długość 1, drugi bok również ma długość 1, a przeciwprostokątna ma długość √2 (około 1.414).

To fundamentalna proporcja. Jeśli pomnożymy każdy element tej proporcji przez dowolną liczbę, otrzymamy poprawne proporcje dla trójkąta 45 45 90. Na przykład, jeśli boki mają długość 5, to przeciwprostokątna ma długość 5√2.

Jak Wykorzystać Właściwości Trójkąta 45 45 90 w Praktyce?

Właściwości trójkąta 45 45 90 znajdują zastosowanie w wielu dziedzinach. Oto kilka przykładów:

Architektura i Budownictwo: Trójkąty 45 45 90 są wykorzystywane do projektowania budynków, mostów i innych konstrukcji. Zapewniają one stabilność i wytrzymałość. Na przykład, ustawienie podpory pod kątem 45 stopni często poprawia nośność konstrukcji.
Inżynieria: Inżynierowie używają trójkątów 45 45 90 do obliczania odległości, wysokości i kątów. Są one przydatne w projektowaniu maszyn, urządzeń i systemów.
Matematyka i Geometria: Trójkąt 45 45 90 jest doskonałym narzędziem do nauki geometrii i trygonometrii. Pomaga zrozumieć pojęcia takie jak sinus, cosinus i tangens.
Rzemiosło i Majsterkowanie: Podczas cięcia drewna, metalu lub innych materiałów pod kątem 45 stopni, wykorzystanie trójkąta 45 45 90 zapewnia precyzję i dokładność.
Nawigacja: W prostych systemach nawigacyjnych, trójkąt 45 45 90 może pomóc w obliczaniu odległości i kierunków.

Przykłady Zastosowań:

Obliczanie wysokości masztu: Stojąc w pewnej odległości od masztu i mierząc kąt pod jakim widać wierzchołek masztu (45 stopni), możemy stwierdzić, że wysokość masztu jest równa odległości, od której prowadzimy pomiar (zakładając, że mierzymy od poziomu gruntu).
Wyznaczanie przekątnej kwadratu: Jeśli znamy długość boku kwadratu, możemy obliczyć długość jego przekątnej, mnożąc długość boku przez √2.
Konstruowanie schodów: Projektując schody, często wykorzystuje się trójkąty 45 45 90 do zapewnienia odpowiedniego nachylenia i wygody użytkowania.

Przykładowe Zadania i Rozwiązania

Aby lepiej zrozumieć, jak działają właściwości trójkąta 45 45 90, rozwiążmy kilka przykładowych zadań:

Zadanie 1: Jeden z boków trójkąta 45 45 90 ma długość 7 cm. Oblicz długość pozostałych boków.

Rozwiązanie: Ponieważ jest to trójkąt 45 45 90, drugi bok również ma długość 7 cm. Przeciwprostokątna ma długość 7√2 cm, co w przybliżeniu daje 9.9 cm.

Zadanie 2: Przeciwprostokątna trójkąta 45 45 90 ma długość 10 cm. Oblicz długość jego boków.

Rozwiązanie: Wiemy, że przeciwprostokątna ma długość a√2. Zatem a√2 = 10. Dzieląc obie strony równania przez √2, otrzymujemy a = 10/√2. Usuwając niewymierność z mianownika (mnożąc licznik i mianownik przez √2), otrzymujemy a = 5√2 cm, co w przybliżeniu daje 7.07 cm. Zatem każdy z boków ma długość około 7.07 cm.

Zadanie 3: Kwadrat ma bok długości 4 cm. Oblicz długość jego przekątnej.

Rozwiązanie: Przekątna kwadratu dzieli go na dwa trójkąty 45 45 90. Zatem przekątna jest przeciwprostokątną trójkąta 45 45 90 o boku 4 cm. Długość przekątnej wynosi 4√2 cm, co w przybliżeniu daje 5.66 cm.

Dlaczego Warto Znać Trójkąt 45 45 90?

Zrozumienie właściwości trójkąta 45 45 90 przynosi wiele korzyści:

Ułatwia obliczenia: Pozwala szybko i łatwo obliczyć długości boków trójkąta bez konieczności używania skomplikowanych wzorów trygonometrycznych.
Poprawia zrozumienie geometrii: Pomaga w zrozumieniu podstawowych pojęć geometrycznych i trygonometrycznych.
Przydaje się w praktycznych zastosowaniach: Znajduje zastosowanie w wielu dziedzinach, od architektury i budownictwa po rzemiosło i majsterkowanie.
Rozwija umiejętności rozwiązywania problemów: Uczy logicznego myślenia i rozwiązywania problemów geometrycznych.

Podsumowanie

Trójkąt 45 45 90 to fascynujący i użyteczny kształt. Jego proste właściwości pozwalają na szybkie i łatwe obliczenia, a jego zastosowania są szerokie i różnorodne. Pamiętaj o kluczowym związku między bokami: 1 : 1 : √2. Dzięki temu zrozumieniu, będziesz mógł z łatwością rozwiązywać problemy geometryczne, projektować konstrukcje i wykonywać zadania praktyczne.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć właściwości trójkąta 45 45 90. Teraz, uzbrojony w tę wiedzę, możesz z powodzeniem wykorzystywać ją w swoim życiu codziennym i zawodowym. Powodzenia!