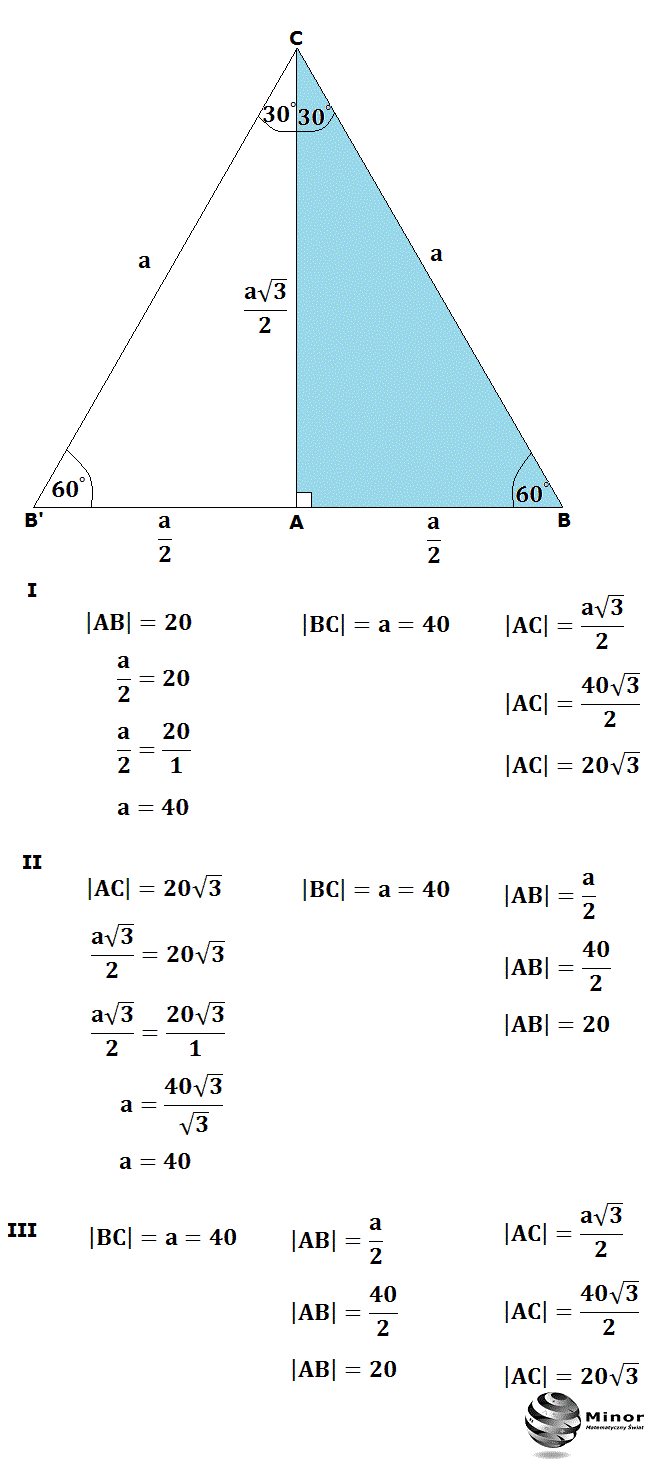Trojkat 30 60 I 90 Stopni

Zmagasz się z zadaniami z geometrii? Masz wrażenie, że wzory z sinusem i cosinusem to czarna magia? A może po prostu chcesz zrozumieć, jak działa jeden z najbardziej przydatnych trójkątów w matematyce? Rozumiem, frustracja potrafi być spora. Ale spokojnie, dzisiaj rozszyfrujemy trójkąt 30 60 90 stopni – krok po kroku, prosto i bez zbędnego zamieszania.

Ten specyficzny trójkąt prostokątny, choć wygląda niepozornie, kryje w sobie mnóstwo matematycznych sekretów. Jego boki pozostają w stałej, przewidywalnej relacji, co sprawia, że rozwiązywanie wielu problemów staje się dziecinnie proste. Brzmi obiecująco? To zaczynajmy!

Czym jest trójkąt 30 60 90 stopni?

Najprościej mówiąc, jest to trójkąt prostokątny, którego kąty mają miary 30, 60 i 90 stopni. Kąt prosty (90 stopni) to podstawa, a pozostałe dwa kąty, 30 i 60 stopni, dopełniają go do 180 stopni – czyli sumy kątów w każdym trójkącie. To, co czyni go wyjątkowym, to stosunek długości jego boków.

Stosunek długości boków

To jest kluczowa informacja, która ułatwia rozwiązywanie zadań. W trójkącie 30 60 90 stopni obowiązuje następująca zasada:

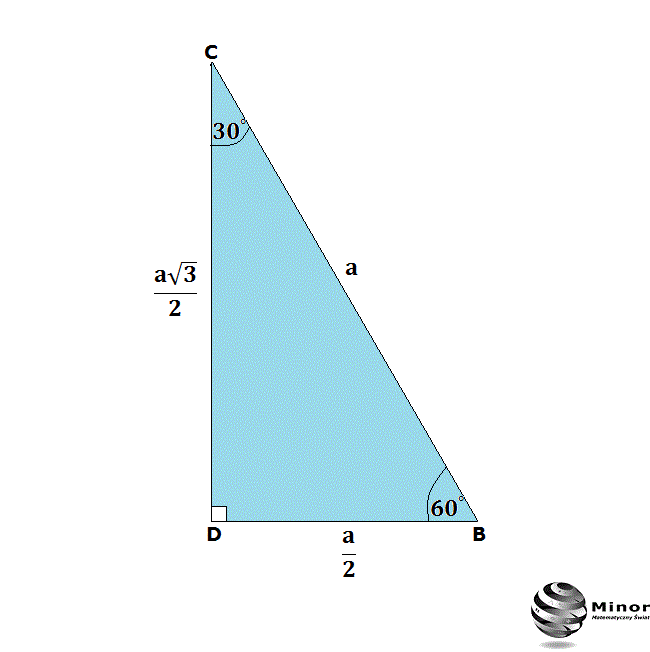
• Najkrótszy bok (naprzeciw kąta 30 stopni): Nazwiemy go a.
• Dłuższa przyprostokątna (naprzeciw kąta 60 stopni): Jej długość to a√3.
• Przeciwprostokątna (naprzeciw kąta 90 stopni): Jej długość to 2a.

Zauważ, że wystarczy znać długość jednego boku, aby obliczyć długości pozostałych! To ogromne ułatwienie.

Przykład: Jeśli najkrótszy bok trójkąta (a) ma długość 5, to:

• Dłuższa przyprostokątna ma długość 5√3.
• Przeciwprostokątna ma długość 10.

Dlaczego trójkąt 30 60 90 jest taki ważny?

Trójkąt 30 60 90 stopni pojawia się w wielu dziedzinach matematyki i fizyki. Oto kilka przykładów:

• Geometria: Obliczanie pól i obwodów figur, szczególnie tych, które składają się z trójkątów równobocznych (które można podzielić na dwa trójkąty 30 60 90).
• Trygonometria: Wartości funkcji trygonometrycznych dla kątów 30 i 60 stopni są łatwe do wyprowadzenia właśnie z tego trójkąta.
• Fizyka: Rozkład sił na składowe, obliczanie wektorów prędkości i przyspieszenia.
• Architektura i inżynieria: Konstrukcje budynków, mostów i innych obiektów często wykorzystują trójkąty dla stabilności i wytrzymałości.

Wiedza o trójkącie 30 60 90 stopni przyspiesza rozwiązywanie wielu problemów i pozwala na lepsze zrozumienie zależności geometrycznych.

Jak rozwiązywać zadania z trójkątem 30 60 90? Praktyczne wskazówki

Najważniejsze to zapamiętać stosunek długości boków: a, a√3, 2a. Oto kilka kroków, które pomogą Ci w rozwiązywaniu zadań:

1. Zidentyfikuj trójkąt: Upewnij się, że masz do czynienia z trójkątem prostokątnym o kątach 30, 60 i 90 stopni.
2. Oznacz boki: Zaznacz najkrótszy bok (naprzeciw kąta 30 stopni) jako a.
3. Wykorzystaj stosunek boków: Jeśli znasz długość jednego boku, możesz obliczyć długości pozostałych, korzystając ze wzorów:
   • Dłuższa przyprostokątna = a√3
   • Przeciwprostokątna = 2a
4. Sprawdź odpowiedź: Upewnij się, że Twoje wyniki mają sens. Czy długość przeciwprostokątnej jest najdłuższa? Czy dłuższa przyprostokątna jest dłuższa od najkrótszego boku?

Przykład: Trójkąt 30 60 90 ma przeciwprostokątną o długości 12. Oblicz długości pozostałych boków.

Rozwiązanie:

1. Wiemy, że przeciwprostokątna to 2a, więc 2a = 12.
2. Dzielimy obie strony równania przez 2: a = 6.
3. Najkrótszy bok (a) ma długość 6.
4. Dłuższa przyprostokątna ma długość a√3 = 6√3.

Odpowiedź: Najkrótszy bok ma długość 6, a dłuższa przyprostokątna ma długość 6√3.

Skąd się bierze ten magiczny stosunek boków? Dowód

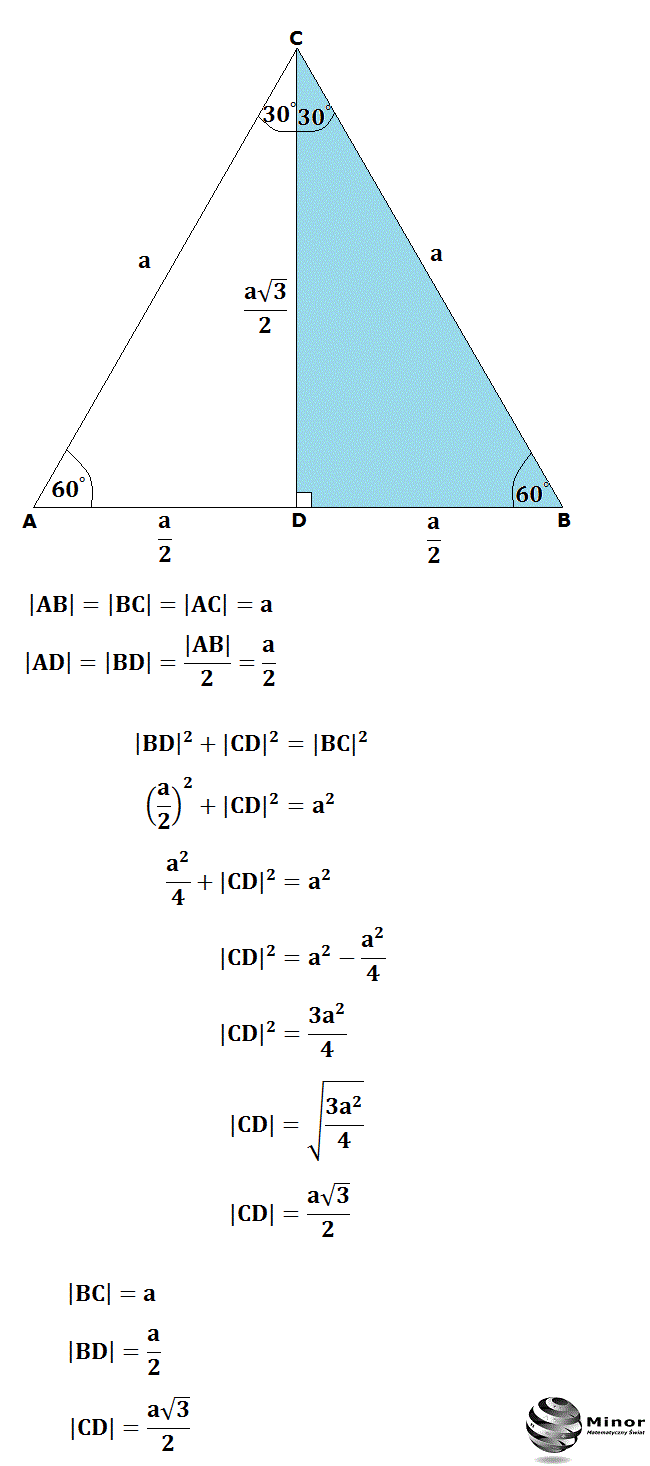
Możesz zastanawiać się, dlaczego stosunek boków w trójkącie 30 60 90 jest akurat taki. Wszystko sprowadza się do trójkąta równobocznego. Wyobraź sobie trójkąt równoboczny, którego wszystkie boki mają długość 2a.

Jeśli przetniesz ten trójkąt na pół, rysując wysokość z jednego wierzchołka na przeciwległy bok, otrzymasz dwa trójkąty prostokątne. Te trójkąty to właśnie trójkąty 30 60 90!

• Przeciwprostokątna: Jest to bok pierwotnego trójkąta równobocznego, czyli ma długość 2a.
• Najkrótszy bok: Jest to połowa boku trójkąta równobocznego, czyli ma długość a.
• Dłuższa przyprostokątna: Można ją obliczyć za pomocą twierdzenia Pitagorasa: (2a)² = a² + x², gdzie x to długość dłuższej przyprostokątnej. Rozwiązując to równanie, otrzymujemy x = a√3.

To dowodzi, że stosunek długości boków w trójkącie 30 60 90 wynosi a, a√3, 2a.

Błędy, których warto unikać

Podczas rozwiązywania zadań z trójkątem 30 60 90 łatwo o pomyłki. Oto kilka najczęstszych błędów i jak ich unikać:

• Pomylenie boków: Upewnij się, że wiesz, który bok jest najkrótszy (naprzeciw kąta 30 stopni), który jest dłuższą przyprostokątną (naprzeciw kąta 60 stopni), a który jest przeciwprostokątną (naprzeciw kąta 90 stopni).
• Błędne obliczenia: Zachowaj ostrożność przy mnożeniu i dzieleniu z pierwiastkiem kwadratowym z 3 (√3). Pamiętaj, że √3 to liczba niewymierna, więc zwykle zostawia się ją w postaci symbolu.
• Zastosowanie niewłaściwego wzoru: Upewnij się, że używasz właściwego wzoru do obliczenia długości boków.
• Ignorowanie jednostek: Pamiętaj o jednostkach (np. centymetry, metry) i upewnij się, że wszystkie boki są wyrażone w tej samej jednostce.

Podsumowanie i dalsza nauka

Gratulacje! Przeszliśmy przez podstawy trójkąta 30 60 90 stopni. Pamiętaj, że kluczem do sukcesu jest praktyka. Rozwiązuj jak najwięcej zadań, aby utrwalić zdobytą wiedzę.

Jeśli chcesz pogłębić swoją wiedzę, polecam:

• Przejrzeć podręczniki do geometrii i trygonometrii.
• Korzystać z zasobów online, takich jak Khan Academy czy YouTube.
• Rozwiązywać zadania z arkuszy maturalnych.

Pamiętaj, że matematyka to nie tylko wzory, ale przede wszystkim logiczne myślenie i rozwiązywanie problemów. Trójkąt 30 60 90 to doskonały przykład, jak proste zasady mogą prowadzić do fascynujących odkryć.

Powodzenia w dalszej nauce! I pamiętaj, nie bój się pytać i szukać odpowiedzi. Matematyka może być naprawdę fascynująca!