Trojkat 30 60 90 Dlugosci Bokow

Czy kiedykolwiek patrzyłeś na budynek, most, lub nawet mebel i zastanawiałeś się, jak inżynierowie i projektanci zdołali osiągnąć tak precyzyjne proporcje? Często odpowiedź kryje się w prostych, lecz potężnych zasadach geometrii. Jedną z tych zasad jest zrozumienie trójkąta o kątach 30, 60 i 90 stopni. Ten trójkąt, ze względu na swoje unikalne właściwości, jest niezwykle użyteczny w wielu dziedzinach, od budownictwa po trigonometrię.

Wiele osób uczących się matematyki ma trudności z zapamiętaniem zależności między bokami trójkąta 30-60-90. Ten artykuł ma na celu wyjaśnić te zależności w sposób jasny, prosty i praktyczny, abyś mógł je łatwo zrozumieć i stosować w rozwiązywaniu zadań.

Zrozumienie Trójkąta 30-60-90

Trójkąt 30-60-90 to specjalny rodzaj trójkąta prostokątnego, co oznacza, że jeden z jego kątów ma 90 stopni. Dwa pozostałe kąty wynoszą odpowiednio 30 i 60 stopni. To specyficzne połączenie kątów sprawia, że stosunki długości jego boków są zawsze takie same, co czyni go bardzo przewidywalnym i użytecznym.

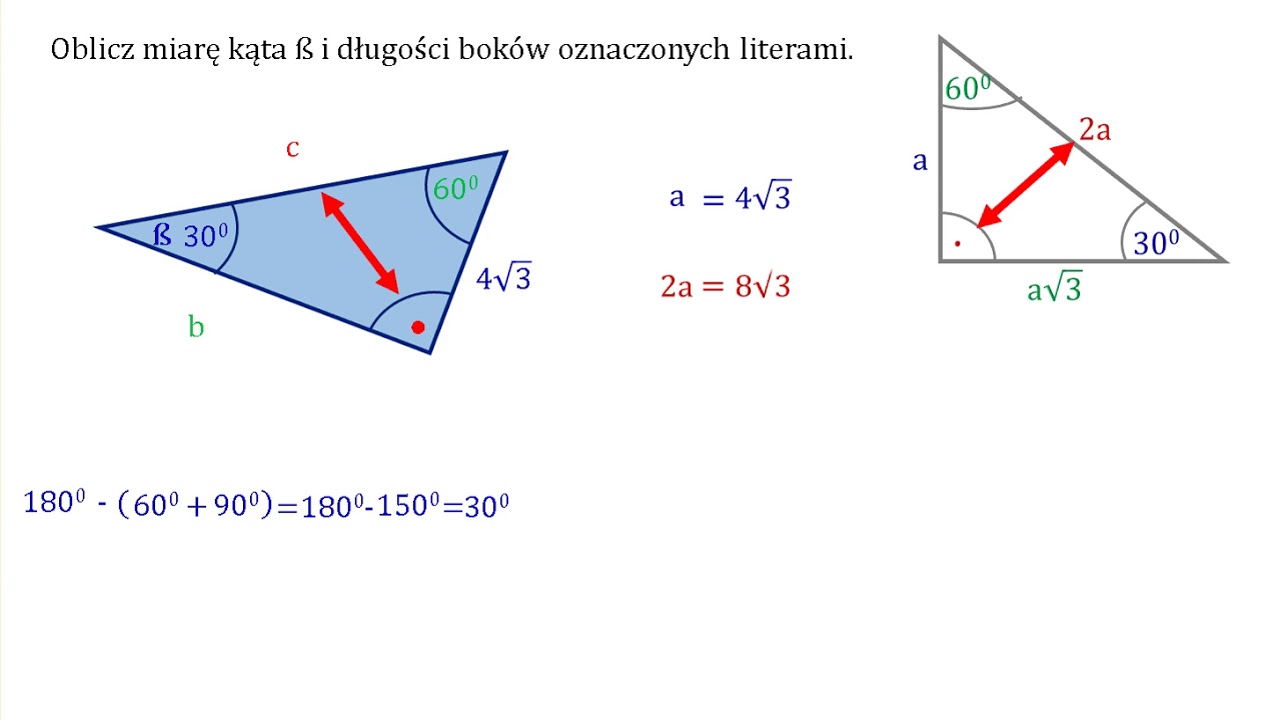
Klucz do zrozumienia trójkąta 30-60-90 leży w zależnościach między jego bokami: przyprostokątną naprzeciw kąta 30 stopni, przyprostokątną naprzeciw kąta 60 stopni i przeciwprostokątną (bokiem naprzeciw kąta prostego).

Zależności Długości Boków

Oto fundamentalna zasada dotycząca długości boków trójkąta 30-60-90:

Przyprostokątna naprzeciw kąta 30 stopni (krótsza przyprostokątna): Oznaczmy ją jako a.
Przyprostokątna naprzeciw kąta 60 stopni (dłuższa przyprostokątna): Jej długość wynosi a√3.
Przeciwprostokątna: Jej długość wynosi 2a.

Czyli, jeśli znasz długość krótszej przyprostokątnej (a), możesz łatwo obliczyć długości pozostałych boków, mnożąc ją odpowiednio przez √3 (pierwiastek z 3) i 2.

Przykład: Załóżmy, że krótsza przyprostokątna (a) ma długość 5 cm. Wtedy:

Dłuższa przyprostokątna ma długość 5√3 cm (około 8.66 cm).
Przeciwprostokątna ma długość 10 cm.

Skąd się biorą te zależności?

Te zależności nie wzięły się znikąd! Można je wyprowadzić, rozważając trójkąt równoboczny. Narysuj trójkąt równoboczny i poprowadź wysokość z jednego wierzchołka na przeciwległy bok. Wysokość podzieli trójkąt równoboczny na dwa identyczne trójkąty prostokątne 30-60-90. Ponieważ wysokość dzieli podstawę trójkąta równobocznego na połowy, możemy zastosować twierdzenie Pitagorasa, aby udowodnić opisane wcześniej zależności.

Praktyczne Zastosowania Trójkąta 30-60-90

Trójkąt 30-60-90 znajduje szerokie zastosowanie w różnych dziedzinach. Oto kilka przykładów:

Budownictwo: Inżynierowie i architekci wykorzystują trójkąt 30-60-90 do obliczania kątów nachylenia dachów, konstrukcji nośnych i innych elementów budynków. Znajomość zależności między bokami ułatwia projektowanie stabilnych i estetycznych struktur.
Nawigacja: W nawigacji morskiej i lotniczej trójkąty 30-60-90 mogą być używane do obliczania odległości i kursów, szczególnie w połączeniu z trigonometrią.
Geometria i Trigonometria: Trójkąt 30-60-90 jest kluczowym elementem wielu zadań z geometrii i trigonometrii. Zrozumienie jego właściwości ułatwia rozwiązywanie problemów dotyczących kątów, długości boków i powierzchni.
Projektowanie: Projektanci graficzni i przemysłowi wykorzystują trójkąt 30-60-90 do tworzenia harmonijnych i proporcjonalnych kompozycji. Jego uniwersalność sprawia, że jest to przydatne narzędzie w procesie projektowania.

Przykład z życia codziennego: Wyobraź sobie, że masz drabinkę opartą o ścianę pod kątem 60 stopni. Jeśli znasz odległość od podstawy drabinki do ściany (która jest krótszą przyprostokątną trójkąta 30-60-90), możesz łatwo obliczyć długość drabinki (przeciwprostokątną) oraz wysokość, na jaką sięga drabinka na ścianie (dłuższą przyprostokątną).

Jak Zapamiętać Zależności?

Zapamiętanie zależności długości boków trójkąta 30-60-90 może wydawać się trudne na początku, ale istnieje kilka sposobów, aby to ułatwić:

Wizualizacja: Narysuj kilka trójkątów 30-60-90 o różnych rozmiarach i oznacz ich boki. Powtarzanie tego procesu pomoże Ci wizualnie zapamiętać zależności.
Mnemotechniki: Stwórz własne mnemotechniki, które pomogą Ci zapamiętać wzory. Na przykład, możesz skojarzyć "krótką" przyprostokątną z liczbą 1, "długą" z pierwiastkiem z 3, a "przeciw" z 2.
Ćwiczenia: Rozwiązuj jak najwięcej zadań z użyciem trójkąta 30-60-90. Im więcej ćwiczysz, tym lepiej utrwalisz sobie zależności.
Zrozumienie, nie zapamiętywanie: Zamiast próbować na siłę zapamiętać wzory, postaraj się zrozumieć, skąd się one biorą (patrz wyprowadzenie z trójkąta równobocznego). Zrozumienie koncepcji jest trwalsze niż samo zapamiętywanie.

Typowe Błędy i Jak Ich Unikać

Podczas pracy z trójkątem 30-60-90 często popełniane są następujące błędy:

Pomylenie kątów: Upewnij się, że wiesz, która przyprostokątna jest naprzeciw którego kąta. Pomylenie kątów prowadzi do błędnych obliczeń.
Nieprawidłowe stosowanie wzorów: Uważaj, aby nie pomylić wzorów na długości boków. Pamiętaj, że dłuższa przyprostokątna to a√3, a nie a√2.
Zaokrąglanie liczb zbyt wcześnie: Jeśli masz do czynienia z pierwiastkami, staraj się zaokrąglać liczby dopiero na końcu obliczeń, aby uniknąć błędów wynikających z zaokrągleń.

Aby uniknąć tych błędów, sprawdzaj swoje obliczenia, rysuj schematy i upewnij się, że rozumiesz, co robisz.

Podsumowanie

Trójkąt 30-60-90 jest potężnym narzędziem w geometrii i ma szerokie zastosowanie w różnych dziedzinach. Zrozumienie zależności między jego bokami pozwala na łatwe rozwiązywanie problemów dotyczących kątów, długości boków i powierzchni.

Pamiętaj o kluczowych zależnościach: przyprostokątna naprzeciw kąta 30 stopni (a), przyprostokątna naprzeciw kąta 60 stopni (a√3) i przeciwprostokątna (2a). Ćwicz regularnie, aby utrwalić wiedzę i uniknąć typowych błędów.

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć trójkąt 30-60-90 i jego zastosowania. Teraz jesteś wyposażony w wiedzę, która pozwoli Ci rozwiązywać zadania i analizować sytuacje, w których występuje ten specjalny trójkąt. Powodzenia!