Trapez Wpisany W Okrąg Własności

Czy kiedykolwiek zastanawiałeś się, jakie specjalne właściwości posiada figura, która łączy w sobie prostotę trapezu i elegancję okręgu? Mówimy o trapezie wpisanym w okrąg. Ten artykuł jest skierowany do uczniów szkół średnich, studentów oraz wszystkich miłośników geometrii, którzy pragną zgłębić wiedzę na temat tej fascynującej figury. Przyjrzymy się jej charakterystycznym cechom, twierdzeniom i zastosowaniom. Zapraszam do lektury!

Podstawowe Definicje i Właściwości Trapezu

Zanim przejdziemy do trapezu wpisanego w okrąg, przypomnijmy sobie definicję trapezu. Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych. Te boki równoległe nazywamy podstawami trapezu, a pozostałe dwa boki to ramiona.

Wyróżniamy różne rodzaje trapezów:

Trapez równoramienny: Trapez, którego ramiona są równej długości.
Trapez prostokątny: Trapez, który ma co najmniej jeden kąt prosty.

Czym Jest Okrąg Opisany na Wielokącie?

Okrąg opisany na wielokącie to okrąg, który przechodzi przez wszystkie wierzchołki tego wielokąta. Innymi słowy, wszystkie wierzchołki wielokąta leżą na okręgu. Nie każdy wielokąt można wpisać w okrąg. Istnieją pewne warunki, które muszą być spełnione, aby taki okrąg istniał.

Trapez Wpisany w Okrąg: Definicja i Podstawowe Twierdzenie

Trapez wpisany w okrąg to trapez, którego wszystkie wierzchołki leżą na okręgu. Brzmi prosto, ale ta definicja pociąga za sobą szereg konsekwencji i ważnych właściwości.

Podstawowe Twierdzenie: Trapez można wpisać w okrąg wtedy i tylko wtedy, gdy jest on trapezem równoramiennym.

To kluczowe twierdzenie jest fundamentem całej teorii trapezu wpisanego w okrąg. Oznacza to, że jeśli trapez jest wpisany w okrąg, to na pewno jest równoramienny. I odwrotnie, jeśli mamy trapez równoramienny, to zawsze możemy na nim opisać okrąg.

Dowód Twierdzenia

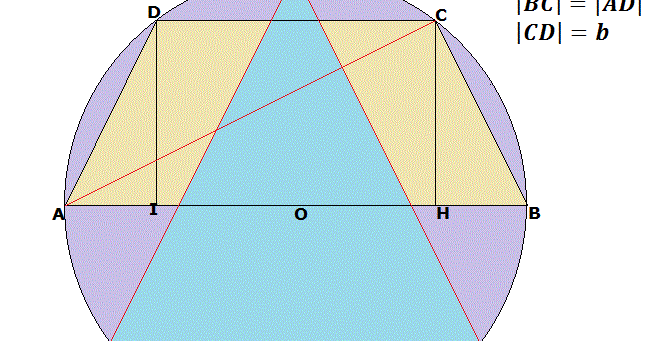
Dowód tego twierdzenia jest dość prosty i elegancki. Rozważmy trapez ABCD, gdzie AB i CD są podstawami, a AD i BC ramionami.

Część 1 (Trapez wpisany w okrąg => Trapez równoramienny): Załóżmy, że trapez ABCD jest wpisany w okrąg. Wtedy kąty BAD i BCD są kątami wpisanymi w okrąg, opartymi na łukach BD i BA. Suma miar tych kątów wynosi 180 stopni (ponieważ są to kąty wewnętrzne czworokąta wpisanego w okrąg). Ponieważ AB || CD, kąty BAD i ADC są kątami przyległymi, a ich suma również wynosi 180 stopni. Zatem kąt BCD = kąt ADC. Analogicznie dowodzimy, że kąt ABC = kąt BAD. Skoro kąty przy podstawie AB są równe, to trapez ABCD jest równoramienny.
Część 2 (Trapez równoramienny => Trapez wpisany w okrąg): Załóżmy, że trapez ABCD jest równoramienny, czyli AD = BC. Poprowadźmy symetralną odcinka AB (podstawy). Ta symetralna przechodzi przez środek okręgu opisanego na trójkącie ABC (ponieważ AB jest cięciwą). Podobnie, symetralna odcinka CD również przechodzi przez środek okręgu opisanego na trójkącie ACD. Ponieważ trapez jest równoramienny, symetralne AB i CD się pokrywają. Zatem istnieje jeden okrąg, który przechodzi przez wszystkie cztery wierzchołki trapezu.

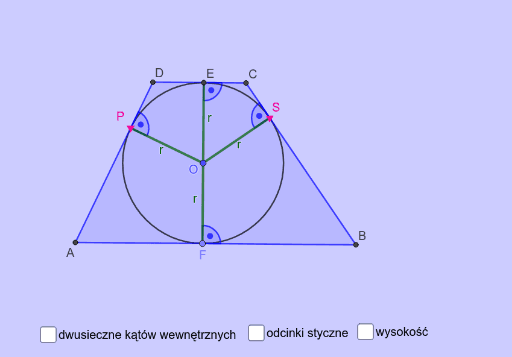
Własności Trapezu Równoramiennego Wpisanego w Okrąg

Skoro już wiemy, że trapez wpisany w okrąg musi być równoramienny, możemy przyjrzeć się bliżej jego specjalnym właściwościom:

Równość kątów przy podstawie: Kąty przy każdej z podstaw są sobie równe. Czyli, ∠BAD = ∠ABC i ∠ADC = ∠BCD.
Równość przekątnych: Przekątne trapezu równoramiennego są równej długości. Czyli, AC = BD.
Wysokość trapezu: Wysokość trapezu równoramiennego opuszczona z wierzchołka krótszej podstawy dzieli dłuższą podstawę na dwa odcinki, z których jeden jest równy średniej arytmetycznej długości podstaw, a drugi jest równy połowie różnicy długości podstaw.
Środek okręgu opisanego: Środek okręgu opisanego na trapezie leży na symetralnej podstaw.

Zastosowania Trapezu Wpisanego w Okrąg

Wiedza o trapezie wpisanym w okrąg przydaje się w rozwiązywaniu zadań geometrycznych, a także w problemach inżynierskich i architektonicznych. Przykłady:

Obliczanie pola i obwodu trapezu: Znając promień okręgu opisanego i długości boków trapezu, możemy obliczyć jego pole i obwód.
Wyznaczanie kątów w trapezie: Jeśli wiemy, że trapez jest wpisany w okrąg i znamy miarę jednego z kątów, możemy wyznaczyć miary pozostałych kątów.
Konstrukcje geometryczne: Umiejętność konstruowania trapezu wpisanego w okrąg może być przydatna w zadaniach konstrukcyjnych.
Architektura: Elementy w kształcie trapezu wpisanego w okrąg można spotkać w projektach architektonicznych, np. w kształtach okien, dachów czy dekoracji.

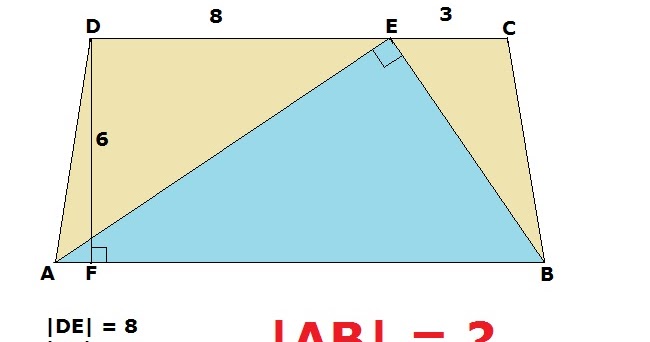
Przykładowe Zadanie

Zadanie: Trapez ABCD jest wpisany w okrąg. Dłuższa podstawa AB ma długość 10 cm, krótsza podstawa CD ma długość 4 cm, a ramię AD ma długość 5 cm. Oblicz długość ramienia BC oraz wysokość trapezu.

Rozwiązanie:

Skoro trapez jest wpisany w okrąg, to jest trapezem równoramiennym, więc BC = AD = 5 cm.
Poprowadźmy wysokości DE i CF z wierzchołków D i C na podstawę AB.
Odcinek AE = FB = (AB - CD) / 2 = (10 - 4) / 2 = 3 cm.
W trójkącie prostokątnym ADE: DE² = AD² - AE² = 5² - 3² = 16, więc DE = 4 cm.
Wysokość trapezu wynosi 4 cm.

Podsumowanie

Trapez wpisany w okrąg to szczególna i fascynująca figura geometryczna, charakteryzująca się szeregiem unikalnych właściwości. Pamiętajmy, że kluczem do zrozumienia tej figury jest twierdzenie, że trapez można wpisać w okrąg wtedy i tylko wtedy, gdy jest on trapezem równoramiennym. Znajomość tych właściwości pozwala na efektywne rozwiązywanie zadań geometrycznych i znajdowanie praktycznych zastosowań w różnych dziedzinach. Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć tę ciekawą figurę. Zachęcam do dalszego eksplorowania świata geometrii! Powodzenia w nauce i rozwiązywaniu zadań!