Trapez Prostokątny Wzór Na Pole

Czy zastanawiałeś się kiedyś, jak obliczyć pole trapezu prostokątnego? Ten artykuł jest dla Ciebie! Niezależnie od tego, czy jesteś uczniem przygotowującym się do sprawdzianu z geometrii, studentem potrzebującym odświeżenia wiedzy, czy po prostu osobą ciekawą świata i chcącą poszerzyć swoje umiejętności matematyczne, ten przewodnik krok po kroku wyjaśni Ci wszystko, co musisz wiedzieć o wzorze na pole trapezu prostokątnego. Przygotuj się na jasne i zrozumiałe wyjaśnienia, przykłady z życia wzięte i praktyczne wskazówki, które pomogą Ci opanować tę umiejętność. Zaczynamy!

Czym jest Trapez Prostokątny? Definicja i Cechy

Zanim przejdziemy do wzoru na pole, upewnijmy się, że rozumiemy, czym dokładnie jest trapez prostokątny. Najprościej mówiąc, jest to czworokąt, który spełnia dwa warunki:

Posiada dokładnie jedną parę boków równoległych (zwanych podstawami).
Ma przynajmniej jeden kąt prosty (90 stopni).

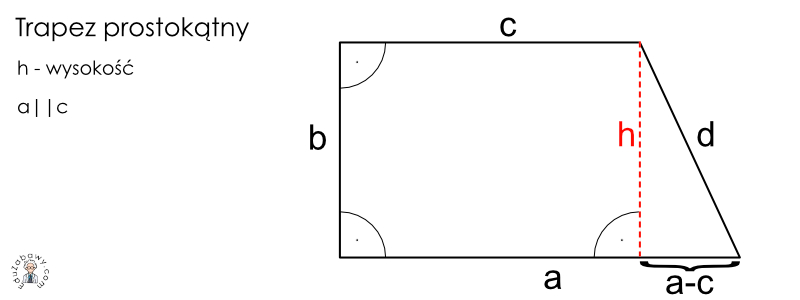
Te dwa warunki definiują trapez prostokątny. Ważne jest, aby zapamiętać, że tylko jedna para boków jest równoległa. Gdyby były dwie pary boków równoległych, mielibyśmy do czynienia z równoległobokiem (a w szczególności, z prostokątem, jeśli wszystkie kąty byłyby proste).

Kluczowe elementy trapezu prostokątnego:

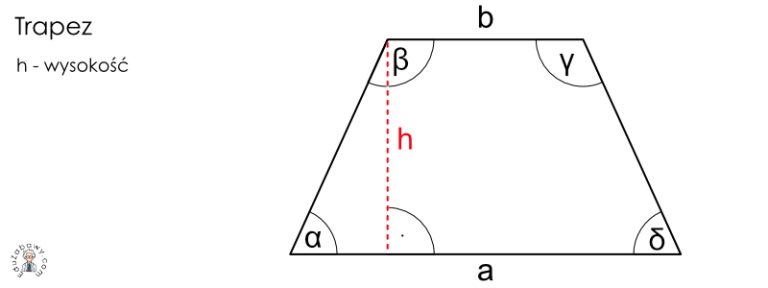
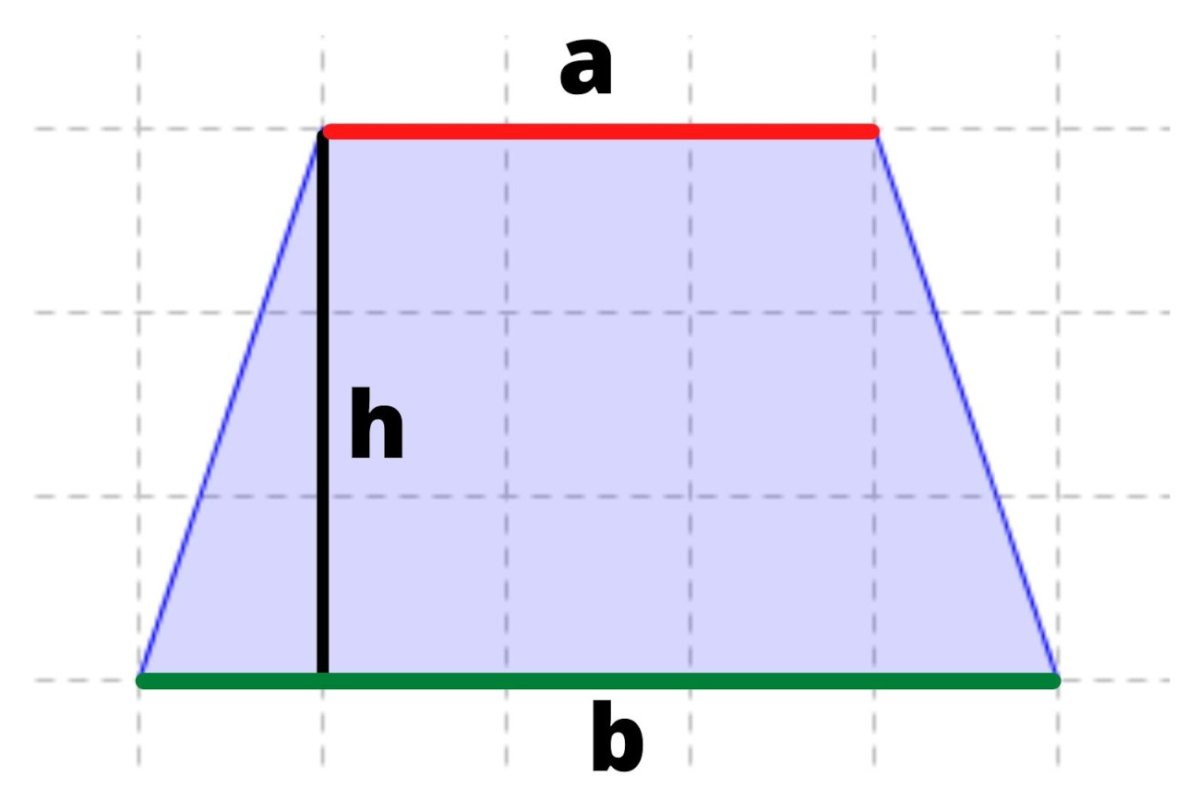
Podstawy: Dwa boki równoległe, o różnych długościach (oznaczane często jako a i b).
Wysokość: Odcinek prostopadły do obu podstaw, łączący je. W trapezie prostokątnym, jeden z boków nierównoległych jest jednocześnie wysokością.
Boki nierównoległe: Dwa pozostałe boki, które nie są równoległe (jeden z nich jest wysokością).
Kąty: Trapez prostokątny ma co najmniej jeden kąt prosty.

Zauważ, że w trapezie prostokątnym wysokość pokrywa się z jednym z boków nierównoległych. To upraszcza obliczenia, ponieważ nie musimy szukać wysokości wewnątrz trapezu – jest ona już widoczna!

Wzór na Pole Trapezu Prostokątnego: Teoria i Praktyka

Teraz, gdy rozumiemy, czym jest trapez prostokątny, możemy przejść do wzoru na obliczanie jego pola. Wzór ten jest bardzo prosty i łatwy do zapamiętania:

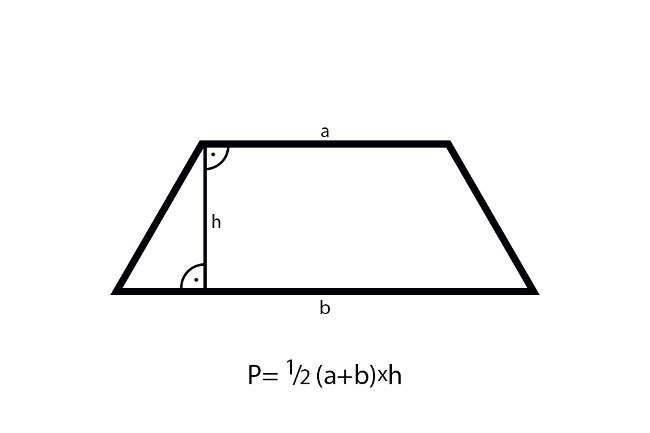
Pole trapezu prostokątnego = (a + b) * h / 2

Gdzie:

a i b to długości podstaw trapezu.
h to wysokość trapezu (długość boku prostopadłego do podstaw).

Inaczej mówiąc, aby obliczyć pole trapezu prostokątnego, musimy:

Zsumować długości obu podstaw (a + b).
Pomnożyć wynik przez wysokość (h).
Podzielić wynik przez 2.

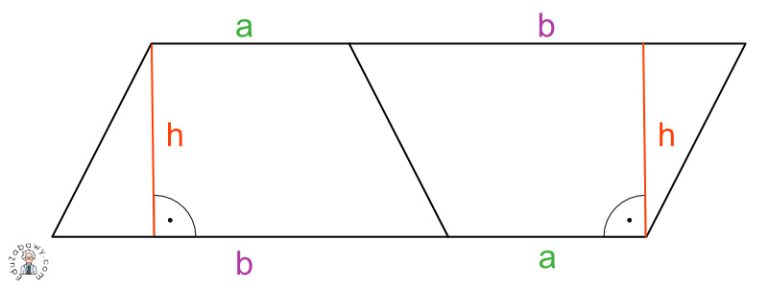
Dlaczego ten wzór działa? Można to zrozumieć, wyobrażając sobie, że "przekształcamy" trapez w prostokąt. Jeśli narysujemy drugi, identyczny trapez prostokątny i obrócimy go tak, aby jego bok pochyły pasował do boku pochyłego pierwszego trapezu, otrzymamy równoległobok. Pole tego równoległoboku jest równe (a+b)*h, a pole jednego trapezu to połowa pola równoległoboku. Stąd wzór (a+b)*h/2.

Przykłady Obliczeń Pola Trapezu Prostokątnego:

Spójrzmy na kilka przykładów, aby lepiej zrozumieć, jak stosować ten wzór w praktyce.

Przykład 1:

Załóżmy, że mamy trapez prostokątny, w którym:

Długość podstawy a = 5 cm
Długość podstawy b = 8 cm
Wysokość h = 4 cm

Aby obliczyć pole, podstawiamy te wartości do wzoru:

Pole = (5 + 8) * 4 / 2 = 13 * 4 / 2 = 52 / 2 = 26 cm²

Zatem pole tego trapezu prostokątnego wynosi 26 cm².

Przykład 2:

Mamy trapez prostokątny o:

Długość podstawy a = 12 m
Długość podstawy b = 7 m
Wysokość h = 6 m

Obliczamy pole:

Pole = (12 + 7) * 6 / 2 = 19 * 6 / 2 = 114 / 2 = 57 m²

Pole tego trapezu prostokątnego to 57 m².

Przykład 3: (Przykład z życia wzięty)

Wyobraź sobie, że projektujesz rampę dla wózka inwalidzkiego. Rampa ma kształt trapezu prostokątnego. Dolna podstawa (a) ma długość 3 metry, górna podstawa (b) ma długość 1 metr, a wysokość (h) rampy wynosi 0.5 metra. Jakie jest pole powierzchni tej rampy?

Pole = (3 + 1) * 0.5 / 2 = 4 * 0.5 / 2 = 2 / 2 = 1 m²

Pole powierzchni rampy wynosi 1 m².

Praktyczne Zastosowania Wzoru na Pole Trapezu Prostokątnego

Wzór na pole trapezu prostokątnego nie jest tylko teoretycznym ćwiczeniem matematycznym. Ma wiele praktycznych zastosowań w różnych dziedzinach życia.

Architektura i Budownictwo: Obliczanie powierzchni dachów, ścian, podłóg o nieregularnych kształtach (np. fragmenty dachu w kształcie trapezu prostokątnego).
Inżynieria: Projektowanie ramp, mostów, tuneli, gdzie elementy mogą mieć kształt trapezu prostokątnego.
Rolnictwo: Obliczanie powierzchni pól o nieregularnych granicach.
Projektowanie Graficzne: Określanie powierzchni elementów graficznych o kształcie trapezu prostokątnego.
Geodezja: Obliczanie powierzchni działek i terenów.
Stolarstwo i Rzemiosło: Tworzenie elementów dekoracyjnych, mebli, gdzie precyzyjne obliczenia powierzchni są kluczowe.

Wyobraź sobie, że planujesz zbudować mały domek narzędziowy w ogrodzie. Jedna ze ścian ma kształt trapezu prostokątnego ze względu na nachylenie dachu. Aby oszacować ilość materiału (np. desek) potrzebnych do zbudowania tej ściany, musisz obliczyć jej powierzchnię, czyli pole trapezu prostokątnego. Bez tej wiedzy, narażasz się na kupno zbyt dużej lub zbyt małej ilości materiału, co wiąże się z dodatkowymi kosztami lub opóźnieniami w budowie.

Wskazówki i Triki dotyczące Obliczania Pola Trapezu Prostokątnego

Oto kilka wskazówek, które mogą Ci pomóc w obliczaniu pola trapezu prostokątnego:

Upewnij się, że dobrze identyfikujesz podstawy i wysokość: Najczęstszym błędem jest pomylenie boków równoległych z nierównoległymi lub nieprawidłowe zidentyfikowanie wysokości.
Zwróć uwagę na jednostki: Wszystkie wymiary (podstawy i wysokość) muszą być wyrażone w tej samej jednostce (np. centymetry, metry, cale). Jeśli masz wymiary w różnych jednostkach, najpierw je przelicz na jedną jednostkę.
Sprawdź wynik: Po obliczeniu pola, upewnij się, że wynik ma sens. Czy pole jest realne w kontekście wymiarów trapezu?
Używaj kalkulatora: Jeśli masz do czynienia z dużymi lub skomplikowanymi liczbami, użyj kalkulatora, aby uniknąć błędów rachunkowych.
Rozwiąż więcej przykładów: Im więcej przykładów rozwiążesz, tym lepiej zrozumiesz wzór i proces obliczania pola.

Podsumowanie i Wartość Dodana

Gratulacje! Dotarłeś do końca tego artykułu i teraz znasz wzór na pole trapezu prostokątnego oraz wiesz, jak go stosować w praktyce. Pamiętaj, że wiedza matematyczna to potęga. Dzięki umiejętności obliczania pola trapezu prostokątnego możesz rozwiązywać realne problemy w różnych dziedzinach życia, od budownictwa po projektowanie. Nie bój się wykorzystywać tej wiedzy i rozwijać swoich umiejętności matematycznych!

W tym artykule dowiedzieliśmy się:

Czym jest trapez prostokątny i jakie są jego cechy charakterystyczne.
Jaki jest wzór na pole trapezu prostokątnego: Pole = (a + b) * h / 2.
Jak stosować ten wzór w praktyce, rozwiązując przykłady.
Gdzie można wykorzystać wzór na pole trapezu prostokątnego w życiu codziennym.
Jakie są wskazówki i triki dotyczące obliczania pola.

Mam nadzieję, że ten artykuł był dla Ciebie pomocny i zrozumiały. Pamiętaj, że praktyka czyni mistrza, więc rozwiązuj jak najwięcej zadań, aby utrwalić swoją wiedzę. Powodzenia!