Test Z Matematyki Klasa 5 Ulamki Dziesietne

Witajcie młodzi matematycy! Przygotowujecie się do testu z matematyki w klasie 5, a w szczególności boicie się ułamków dziesiętnych? Bez obaw! Ułamki dziesiętne wcale nie są takie straszne, jak się wydają. W rzeczywistości, używamy ich każdego dnia, często nawet o tym nie wiedząc! Spróbujmy je razem oswoić.

Czym są Ułamki Dziesiętne?

Wyobraź sobie pizzę. Podziel ją na 10 równych kawałków. Jeżeli zjesz jeden kawałek, zjadłeś 1/10 pizzy. Ułamek 1/10 możemy zapisać jako ułamek dziesiętny: 0,1. To właśnie jest ułamek dziesiętny! Ułamek dziesiętny to po prostu sposób zapisywania ułamków, których mianownikami są liczby 10, 100, 1000 i tak dalej. Zamiast kreski ułamkowej, używamy przecinka (w Polsce) lub kropki (w niektórych innych krajach).

Popatrzmy na kilka przykładów:

1/10 = 0,1 (jedna dziesiąta)
3/10 = 0,3 (trzy dziesiąte)
7/10 = 0,7 (siedem dziesiątych)

A co, jeśli podzielimy pizzę na 100 kawałków? Zjedzenie jednego kawałka to 1/100 pizzy, co zapisujemy jako 0,01 (jedna setna). Dwa kawałki to 2/100, czyli 0,02 (dwie setne), a np. 25 kawałków to 25/100, czyli 0,25 (dwadzieścia pięć setnych).

Wizualizacja: Wyobraź sobie tablicę z 100 kwadracikami (jak plansza do gry w statki). Zamaluj jeden kwadracik. Zamalowałeś 0,01 (jedną setną) całej tablicy. Zamaluj 10 kwadracików w rzędzie. Zamalowałeś 0,1 (jedną dziesiątą) tablicy, czyli 10 setnych.

Zapis Ułamków Dziesiętnych

Ułamki dziesiętne mają swoją strukturę. Spójrzmy na przykład: 3,14

3 to część całkowita. To, co jest przed przecinkiem, to całe liczby.
, to przecinek dziesiętny. Oddziela część całkowitą od części ułamkowej.
1 to cyfra dziesiątek. Oznacza 1/10.
4 to cyfra setnych. Oznacza 4/100.

Zatem 3,14 to 3 całe i 14 setnych. Można to zapisać również jako 3 i 14/100.

Inny przykład: 0,75. To 0 całych i 75 setnych, czyli 75/100. Możemy to jeszcze uprościć – 75/100 = 3/4 (trzy czwarte). Widzisz, jak ułamki zwykłe i dziesiętne są ze sobą powiązane?

Ułamki Dziesiętne w Życiu Codziennym

Ułamki dziesiętne otaczają nas zewsząd! Gdzie je spotykamy?

Pieniądze: Cena produktu to często ułamek dziesiętny, np. 2,50 zł (dwa złote pięćdziesiąt groszy). 50 groszy to 50/100 złotego, czyli pół złotego.
Wzrost: Twój wzrost może wynosić 1,45 m (jeden metr i czterdzieści pięć centymetrów). 45 cm to 45/100 metra.
Waga: Waga owoców w sklepie może być podana jako 0,75 kg (zero kilogramów i siedemdziesiąt pięć dekagramów).
Wyniki sportowe: Czas w biegach, odległość w skoku w dal - wszystko to często mierzymy z dokładnością do ułamków dziesiętnych!

Działania na Ułamkach Dziesiętnych

Dodawanie i Odejmowanie

Dodawanie i odejmowanie ułamków dziesiętnych jest bardzo proste, pod warunkiem, że pamiętamy o jednej ważnej rzeczy: przecinek pod przecinkiem! Ustawiamy ułamki jeden pod drugim tak, aby przecinki znalazły się w jednej linii. Następnie dodajemy lub odejmujemy jak zwykłe liczby.

Przykład: 2,35 + 1,22 = ?

      2,35
    + 1,22
    ------
      3,57

Wynik: 3,57

Przykład: 5,78 - 2,15 = ?

      5,78
    - 2,15
    ------
      3,63

Wynik: 3,63

Jeśli brakuje cyfr po przecinku, możemy dopisać zera. Na przykład: 3 + 1,2 = 3,0 + 1,2 = 4,2

Mnożenie

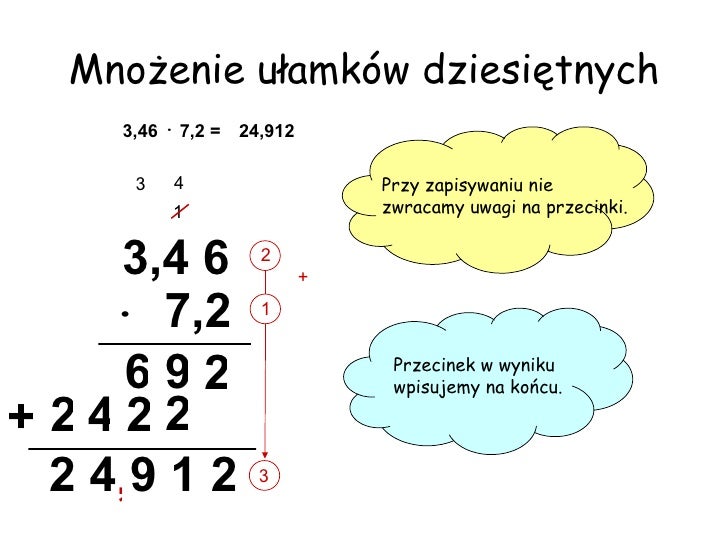
Mnożenie ułamków dziesiętnych wygląda trochę inaczej. Najpierw mnożymy liczby tak, jakby nie było przecinka. Potem liczymy, ile cyfr jest łącznie po przecinku w obu liczbach, które mnożyliśmy. Tyle samo cyfr musi być po przecinku w wyniku.

Przykład: 2,5 x 1,2 = ?

Mnożymy 25 x 12 = 300
W 2,5 jest 1 cyfra po przecinku, a w 1,2 też 1 cyfra po przecinku. Razem 2 cyfry.
Więc w wyniku, czyli w 300, musimy oddzielić przecinkiem 2 cyfry od końca: 3,00
3,00 to to samo co 3

Wynik: 3

Wizualizacja: Pomyśl o mnożeniu jako o powiększaniu czegoś. Mnożąc 2,5 przez 1,2, powiększamy 2,5 o 1 całą i jeszcze kawałek (0,2).

Podsumowanie

Ułamki dziesiętne są bardzo przydatne i wcale nie takie trudne! Pamiętaj o kilku ważnych rzeczach:

Ułamek dziesiętny to sposób zapisywania ułamków o mianowniku 10, 100, 1000 itd.
Przecinek dziesiętny oddziela część całkowitą od części ułamkowej.
Przy dodawaniu i odejmowaniu przecinek musi być pod przecinkiem.
Przy mnożeniu liczymy cyfry po przecinku.

Ćwicz regularnie, a ułamki dziesiętne przestaną być dla Ciebie zagadką! Powodzenia na teście! Pamiętaj, że każdy może nauczyć się matematyki, wystarczy trochę chęci i cierpliwości.