Test Matematyka Pola Figur Klasa 5

Czy Twój piątoklasista ma trudności z obliczaniem pól figur? Zmaganie się z matematyką, a szczególnie z geometrią, to częsty problem, z którym mierzą się uczniowie na tym etapie edukacji. Pamiętaj, nie jesteś sam! Wielu rodziców i nauczycieli obserwuje podobne wyzwania. Ale nie martw się, zrozumienie koncepcji pól figur jest absolutnie osiągalne, a co ważniejsze, może być nawet przyjemne!

Zanim przejdziemy do konkretnych wskazówek i przykładów, poświęćmy chwilę na zrozumienie, dlaczego to tak ważne. Umiejętność obliczania pól figur to nie tylko zadanie domowe. To fundament dla dalszej nauki matematyki, fizyki, a nawet architektury czy projektowania. Wyobraź sobie, że projektujesz swój wymarzony pokój! Musisz obliczyć, ile farby potrzebujesz, prawda? Albo, ile płytek podłogowych musisz kupić. Bez znajomości pól figur, to byłoby bardzo trudne!

Dlaczego Pola Figur Sprawiają Trudności?

Istnieje kilka powodów, dla których uczniowie klasy piątej mogą mieć problemy z obliczaniem pól figur:

* **Abstrakcja:** Geometria operuje na abstrakcyjnych kształtach, a dzieci w tym wieku często lepiej rozumieją konkretne obiekty. * **Zapamiętywanie wzorów:** Mnogość wzorów na pola różnych figur (kwadrat, prostokąt, trójkąt, równoległobok, trapez) może być przytłaczająca. * **Brak zrozumienia podstawowych pojęć:** Często problemem jest słabe zrozumienie pojęcia pola jako miary powierzchni. * **Trudności z operacjami arytmetycznymi:** Obliczanie pól wymaga wykonywania mnożenia i dzielenia, które samo w sobie może sprawiać trudności. * **Lęk przed matematyką:** Negatywne nastawienie do matematyki może blokować proces uczenia się.

Kluczowe Figury Geometryczne w Klasie 5

W klasie piątej uczniowie najczęściej spotykają się z następującymi figurami:

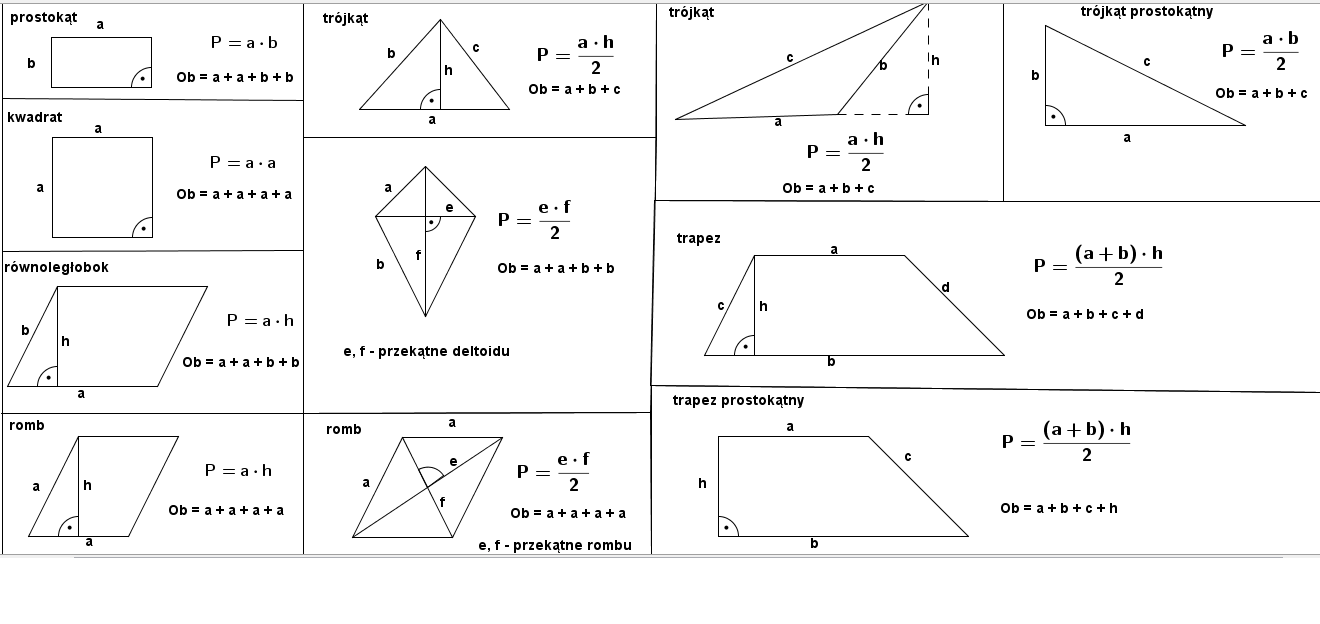
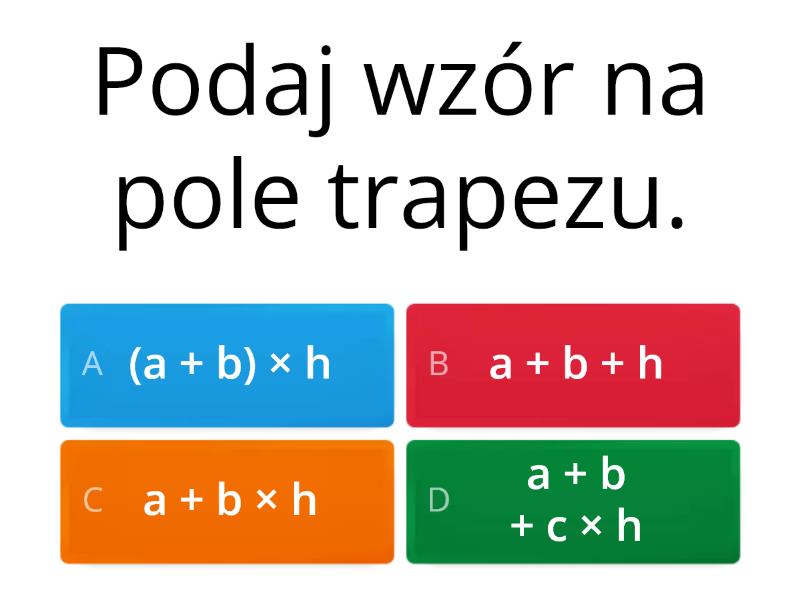
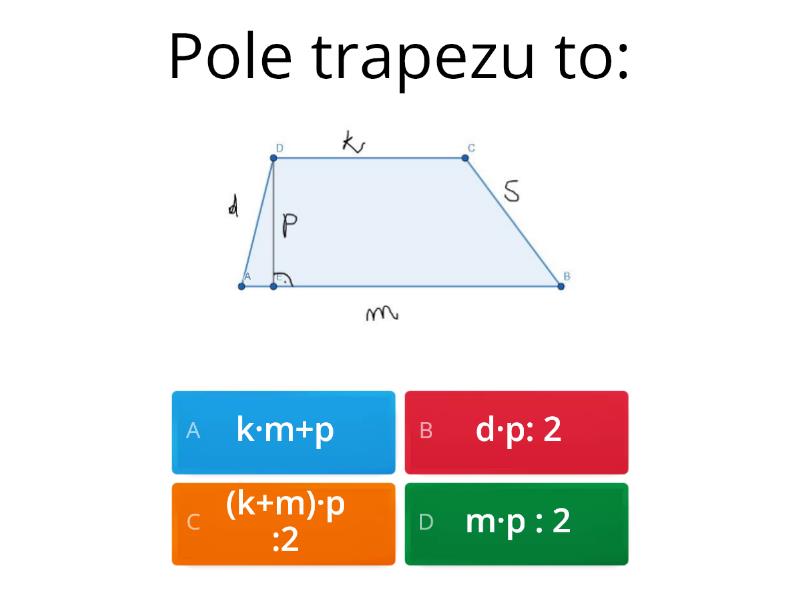
* Kwadrat: Wszystkie boki równe, kąty proste. Pole = bok * bok (a*a). * Prostokąt: Przeciwległe boki równe, kąty proste. Pole = długość * szerokość (a*b). * Trójkąt: Trzy boki, trzy kąty. Pole = (podstawa * wysokość) / 2 ((a*h)/2). Ważne, aby umieć rozpoznać podstawę i wysokość. * Równoległobok: Przeciwległe boki równoległe. Pole = podstawa * wysokość (a*h). Podobnie jak w trójkącie, kluczowe jest prawidłowe zidentyfikowanie wysokości. * Trapez: Dwa boki równoległe (podstawy). Pole = ((podstawa a + podstawa b) * wysokość) / 2 (((a+b)*h)/2).

Praktyczne Wskazówki i Techniki Uczenia

Oto kilka sprawdzonych metod, które pomogą Twojemu dziecku opanować obliczanie pól figur:

* **Zacznij od konkretów:** Zamiast od razu przechodzić do wzorów, wykorzystaj przedmioty codziennego użytku. Mierzenie powierzchni stołu, dywanu czy kartki papieru pozwoli na zrozumienie idei pola. * Wizualizacja:** Narysuj figury, pokoloruj je, wytnij z papieru. Im więcej zmysłów zaangażujesz, tym lepiej uczeń zrozumie. Użyj kolorowych pisaków lub kredek, aby wyróżnić podstawę i wysokość w trójkątach i równoległobokach. * **Podziel figury:** Złożone figury można podzielić na prostsze kształty, takie jak prostokąty i trójkąty. Oblicz pole każdej części oddzielnie, a następnie dodaj wyniki. To technika szczególnie przydatna w zadaniach z trapezami i innymi nieregularnymi figurami. * **Wykorzystaj gry i aplikacje edukacyjne:** Istnieje wiele interaktywnych narzędzi, które sprawiają, że nauka matematyki jest przyjemna i angażująca. Wyszukaj aplikacje i gry związane z geometrią i polami figur. * Stwórz własne zadania:** Wymyślaj zadania związane z otaczającym światem. "Oblicz, ile tapety potrzebujemy na ścianę w pokoju." albo "Ile trawy potrzebujemy, aby obsiać nasz ogródek (zakładając, że ma kształt prostokąta)?". To motywuje i pokazuje praktyczne zastosowanie matematyki. * **Regularna powtórka:** Powtarzaj materiał regularnie, nawet po jego opanowaniu. Krótkie, codzienne ćwiczenia są bardziej efektywne niż długie, sporadyczne sesje. * **Daj czas i bądź cierpliwy:** Każdy uczy się w swoim tempie. Nie zniechęcaj się, jeśli postępy nie są natychmiastowe. Ważne jest, aby dziecko czuło wsparcie i zachętę. * Zrozumienie zamiast pamięciówki:** Staraj się, aby dziecko rozumiało, skąd biorą się wzory, a nie tylko je zapamiętywało. Wyjaśnij, dlaczego pole kwadratu to bok * bok, a nie tylko powtarzaj wzór. * Wykorzystaj pomoce wizualne do wzorów:** Dla każdego wzoru stwórz rysunek ilustrujący, co oznaczają poszczególne elementy (podstawa, wysokość, bok). To ułatwi zapamiętywanie. * Podkreśl ważność jednostek:** Upewnij się, że dziecko pamięta o podawaniu jednostek pola (cm², m², itp.). Brak jednostek to częsty błąd. * Pracuj z przykładami krok po kroku:** Rozwiązuj zadania razem z dzieckiem, krok po kroku, tłumacząc każdy etap. Pozwól mu na samodzielne rozwiązywanie zadań dopiero po zrozumieniu procesu. * Wzmocnienie pozytywne:** Chwal za wysiłek, a nie tylko za wynik. Motywuj do dalszej pracy, nawet jeśli nie wszystko od razu wychodzi.
Przykładowe Zadanie i Rozwiązanie

Zadanie: Pokój ma kształt prostokąta o długości 4 metry i szerokości 3 metry. Ile metrów kwadratowych wykładziny potrzeba, aby pokryć całą podłogę?

Rozwiązanie:

Rozpoznajemy figurę: prostokąt.

Przypominamy sobie wzór na pole prostokąta: Pole = długość * szerokość (a*b).

Podstawiamy dane: Pole = 4 m * 3 m.

Obliczamy: Pole = 12 m².

Odpowiedź: Potrzeba 12 metrów kwadratowych wykładziny.

Mity na Temat Nauki Matematyki

Wiele osób wierzy w mity na temat nauki matematyki, które mogą negatywnie wpływać na podejście do tego przedmiotu. Oto kilka z nich:
* "Matematyka jest tylko dla wybranych": To nieprawda! Każdy może nauczyć się matematyki, jeśli tylko ma odpowiednie wsparcie i motywację. * "Trzeba być geniuszem, żeby dobrze radzić sobie z matematyką": Matematyka to przede wszystkim ciężka praca i systematyczność, a nie wrodzony talent. * "Matematyka jest nudna i nieprzydatna": Matematyka jest wszędzie wokół nas! Od planowania budżetu po gotowanie.
Pamiętaj! Sukces w matematyce to wynik połączenia zrozumienia, praktyki i pozytywnego nastawienia. Nie zniechęcaj się trudnościami, traktuj je jako wyzwania do pokonania. Wspieraj swoje dziecko, bądź cierpliwy i pokaż, że matematyka może być fascynująca i przydatna. Powodzenia!