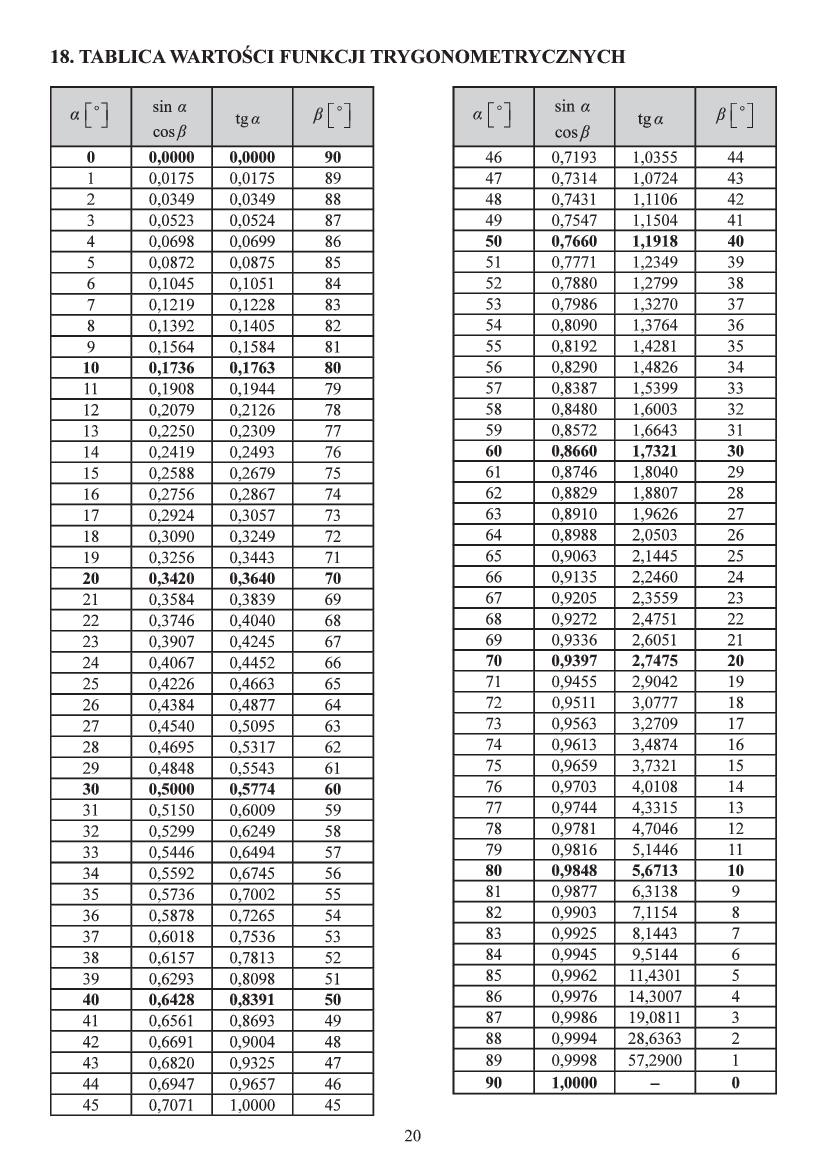
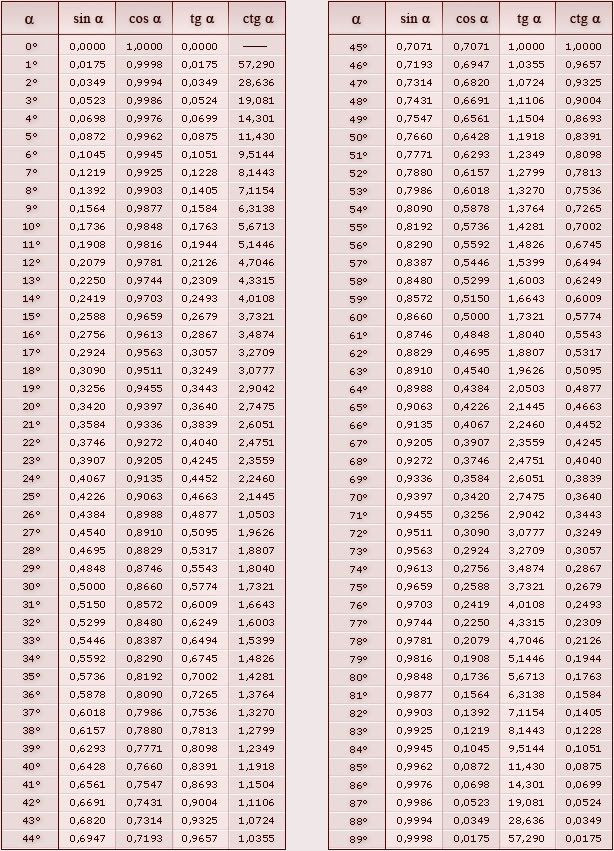
Tablice Wartości Funkcji Trygonometrycznych Dla Kątów Ostrych

Jasne, oto artykuł odpowiadający na twoje polecenie.

Witajcie, drodzy uczniowie! Dzisiaj porozmawiamy o czymś bardzo przydatnym w trygonometrii: o wartościach funkcji trygonometrycznych dla kątów ostrych. Kąt ostry to taki, który ma miarę większą od 0 stopni, ale mniejszą niż 90 stopni. Mówiąc prościej, jest to kąt "mniejszy od kąta prostego". Poznanie wartości funkcji trygonometrycznych dla typowych kątów ostrych ułatwi wam rozwiązywanie wielu zadań. Zaczynajmy!

Zacznijmy od najważniejszych funkcji trygonometrycznych: sinusa (sin), cosinusa (cos) i tangensa (tg). Czasami spotkacie się też z cotangensem (ctg), ale skupimy się głównie na tych trzech podstawowych.

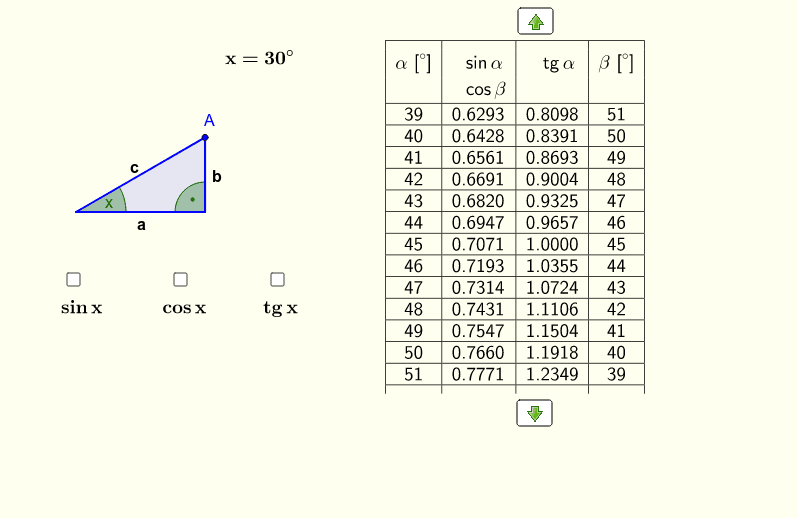
Dla kąta o mierze 30 stopni:

Sinus kąta 30 stopni wynosi 1/2. To bardzo ważna wartość do zapamiętania.
Cosinus kąta 30 stopni wynosi √3/2. Pamiętajcie o pierwiastku z trzech!
Tangens kąta 30 stopni wynosi √3/3. Czyli sinus podzielony przez cosinus.

Dla kąta o mierze 45 stopni:

Sinus kąta 45 stopni wynosi √2/2. Tu mamy pierwiastek z dwóch.
Cosinus kąta 45 stopni również wynosi √2/2. Zauważcie, że sinus i cosinus mają tę samą wartość!
Tangens kąta 45 stopni wynosi 1. Czyli sinus podzielony przez cosinus, a ponieważ są równe, to wynik to 1.

Dla kąta o mierze 60 stopni:

Sinus kąta 60 stopni wynosi √3/2. To jest dokładnie ta sama wartość, co cosinus kąta 30 stopni!
Cosinus kąta 60 stopni wynosi 1/2. To jest dokładnie ta sama wartość, co sinus kąta 30 stopni!
Tangens kąta 60 stopni wynosi √3. Czyli sinus podzielony przez cosinus.

Widzicie pewną zależność? Sinus kąta 30 stopni jest taki sam jak cosinus kąta 60 stopni, i odwrotnie. Podobnie jest z sinusem kąta 60 stopni i cosinusem kąta 30 stopni. To dlatego, że 30 i 60 stopni to kąty dopełniające się do 90 stopni. Ta zależność jest bardzo przydatna!

Jak zapamiętać te wartości?

Zapamiętywanie tych wartości może wydawać się trudne na początku, ale istnieje kilka trików, które mogą wam pomóc:

Skojarzenia: Możecie wymyślić własne skojarzenia. Na przykład, sinus 30 stopni to "pół", bo wynosi 1/2. Cosinus 60 stopni też jest "pół".
Wzory: Starajcie się dostrzegać wzory. Jak wspomnieliśmy, sinus i cosinus zamieniają się wartościami dla kątów dopełniających się do 90 stopni.
Rysunek: Narysujcie sobie trójkąt prostokątny o kątach 30, 60 i 90 stopni. Zaznaczcie długości boków (przeciwprostokątna = 2, krótsza przyprostokątna = 1, dłuższa przyprostokątna = √3). Wtedy łatwo przypomnicie sobie, która wartość przypada na sinus, a która na cosinus. Podobnie narysujcie trójkąt równoramienny prostokątny (45, 45, 90 stopni).
Powtarzanie: Najlepszym sposobem na zapamiętanie czegokolwiek jest po prostu powtarzanie. Przepiszcie te wartości kilka razy, a z czasem wejdą wam w krew.
Używanie w zadaniach: Rozwiązujcie dużo zadań z trygonometrii. Im częściej będziecie używać tych wartości, tym łatwiej je zapamiętacie.

Pamiętajcie też, że tangens to po prostu sinus podzielony przez cosinus. Więc jeśli pamiętacie wartości sinusa i cosinusa, łatwo obliczycie tangens.

A co z cotangensem? Cotangens to odwrotność tangensa, czyli cosinus podzielony przez sinus. Tak więc, ctg(x) = 1/tg(x). Na przykład:

Cotangens kąta 30 stopni wynosi √3. (Odwrotność √3/3)
Cotangens kąta 45 stopni wynosi 1. (Odwrotność 1)
Cotangens kąta 60 stopni wynosi √3/3. (Odwrotność √3)

Wartości funkcji trygonometrycznych dla kątów 0 i 90 stopni:

Dla kąta o mierze 0 stopni:

Sinus kąta 0 stopni wynosi 0.
Cosinus kąta 0 stopni wynosi 1.
Tangens kąta 0 stopni wynosi 0. (Sinus podzielony przez cosinus)

Dla kąta o mierze 90 stopni:

Sinus kąta 90 stopni wynosi 1.
Cosinus kąta 90 stopni wynosi 0.
Tangens kąta 90 stopni nie istnieje (dążymy do nieskończoności), ponieważ dzielimy przez zero.

Zapamiętajcie te wartości, są bardzo często wykorzystywane!

Przykłady zastosowania:

Załóżmy, że macie trójkąt prostokątny, w którym jeden z kątów ostrych ma 30 stopni, a przeciwprostokątna ma długość 10. Chcecie obliczyć długość przyprostokątnej leżącej naprzeciwko kąta 30 stopni.

Wiemy, że sinus kąta 30 stopni to 1/2. Sinus to stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej.

Czyli sin(30°) = przyprostokątna / przeciwprostokątna 1/2 = przyprostokątna / 10 przyprostokątna = 10 * (1/2) = 5

Długość przyprostokątnej wynosi 5.

Inny przykład: Obliczcie wysokość drzewa, jeśli stoicie 20 metrów od niego, a kąt widzenia wierzchołka drzewa wynosi 60 stopni.

W tym przypadku używamy tangensa. Tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przyprostokątnej przyległej do kąta.

tg(60°) = wysokość / odległość √3 = wysokość / 20 wysokość = 20 * √3

Wysokość drzewa wynosi 20√3 metrów.

Mam nadzieję, że ten artykuł pomógł wam zrozumieć wartości funkcji trygonometrycznych dla kątów ostrych i jak je zapamiętać. Pamiętajcie, praktyka czyni mistrza! Rozwiązujcie dużo zadań, a te wartości staną się dla was drugą naturą. Powodzenia!