Systemy Zapisywania Liczb Klasa 4 Gwo

Czy kiedykolwiek zastanawiałeś się, jak ludzie dawniej liczyli, zanim powstały cyfry, których używamy dzisiaj? Albo jak komputery, z których korzystamy na co dzień, rozumieją liczby? To wszystko kwestia systemów zapisywania liczb, temat, który może wydawać się skomplikowany, ale tak naprawdę kryje w sobie fascynującą historię i praktyczne zastosowania. Dla uczniów klasy 4, poznanie tych systemów to ważny krok w zrozumieniu matematyki, ale wiem, że czasem może to być trudne. Spróbujmy więc razem odkryć tajemnice tych systemów, krok po kroku!

Czym są Systemy Zapisywania Liczb?

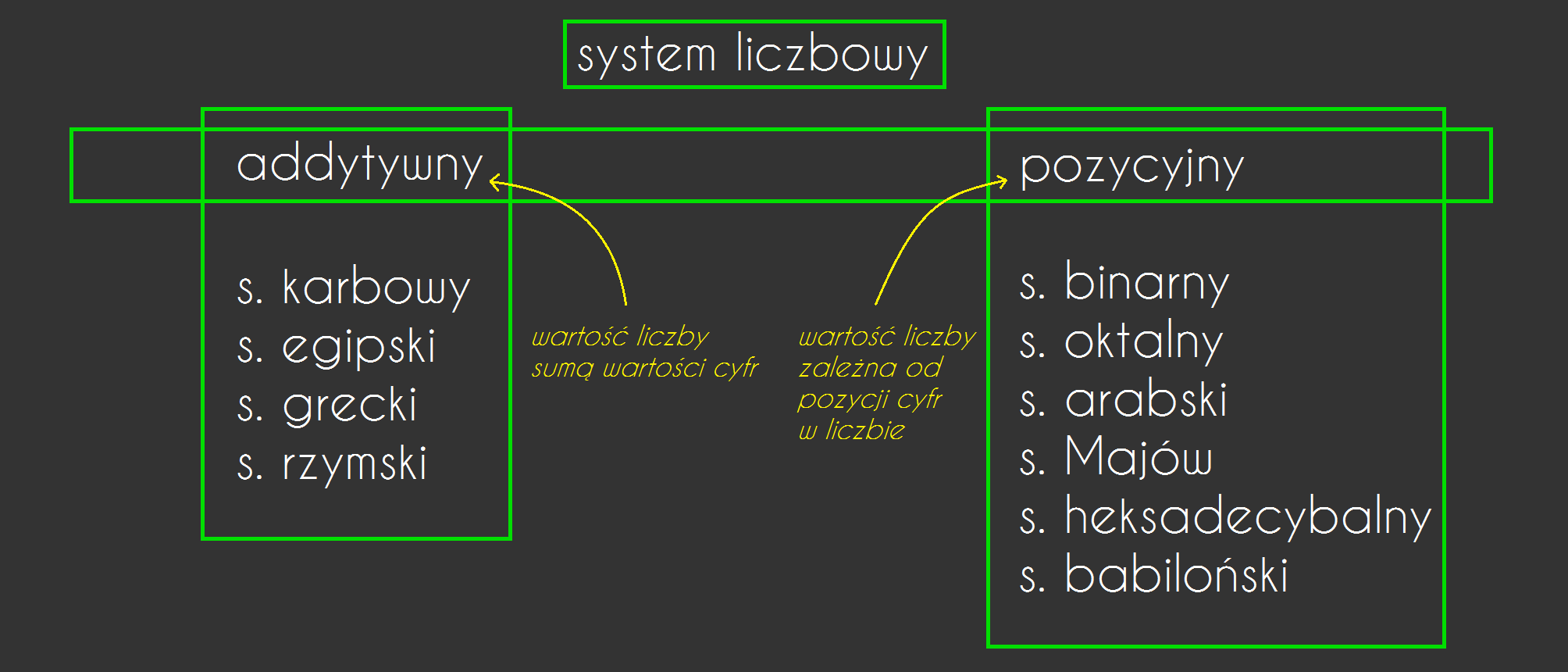
System zapisywania liczb to zbiór reguł i symboli, które pozwalają nam przedstawiać liczby. Mówiąc prościej, to sposób, w jaki zapisujemy liczby, używając różnych znaków. Nasz obecny system, który używamy na co dzień, to system dziesiętny, ale to nie jedyny system, jaki istnieje!

System Dziesiętny: Nasz Codzienny Towarzysz

Prawdopodobnie już wiesz, że w systemie dziesiętnym używamy dziesięciu cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Nazwa "dziesiętny" pochodzi od liczby 10 – to nasza podstawa. Każda pozycja w liczbie ma wartość, która jest potęgą liczby 10. Na przykład, w liczbie 345:

5 oznacza 5 jedności (5 x 10⁰)
4 oznacza 4 dziesiątki (4 x 10¹)
3 oznacza 3 setki (3 x 10²)

Wartość całej liczby to suma tych wartości: 300 + 40 + 5 = 345.

Dlaczego dziesiętny? Prawdopodobnie dlatego, że mamy dziesięć palców u rąk! To całkiem logiczne, prawda?

System Rzymski: Tajemnicze Znaki

Przenieśmy się teraz do starożytnego Rzymu. Rzymianie używali innego systemu zapisywania liczb, który do dziś możemy spotkać na zegarach, w książkach, a nawet na nagrobkach. System rzymski używa liter do reprezentowania liczb:

I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000

Zasady są proste: dodajemy wartości liter, jeśli są ułożone od największej do najmniejszej (np. VI = 5 + 1 = 6), a odejmujemy, jeśli mniejsza litera stoi przed większą (np. IV = 5 - 1 = 4). Na przykład, liczba 19 to XIX (10 + 10 - 1). Złożone? Trochę, ale da się to opanować!

Ćwiczenie: Spróbuj napisać datę swojego urodzenia w systemie rzymskim. Może to być fajna zabawa!

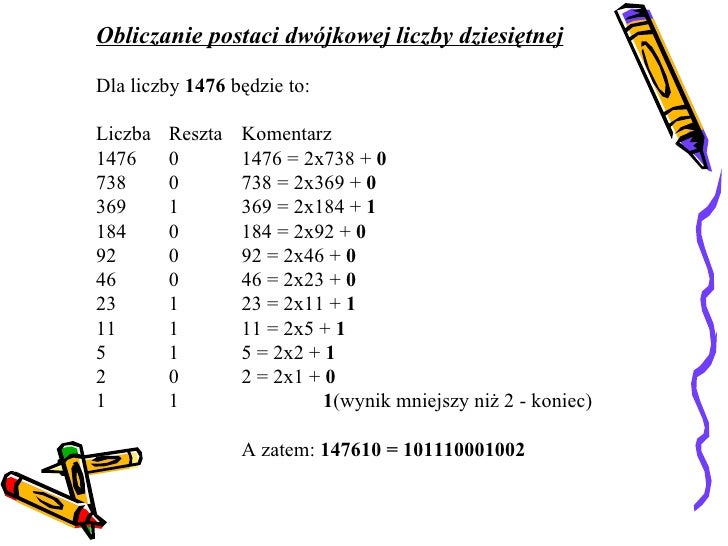
System Dwójkowy: Język Komputerów

Teraz przenieśmy się do świata komputerów. Komputery nie rozumieją liczb w systemie dziesiętnym tak, jak my. Używają systemu dwójkowego, w którym występują tylko dwie cyfry: 0 i 1. Dlaczego? Ponieważ komputery działają na zasadzie włącz/wyłącz (prąd płynie/prąd nie płynie), co idealnie odpowiada 0 i 1.

W systemie dwójkowym każda pozycja ma wartość, która jest potęgą liczby 2. Na przykład, liczba 101 w systemie dwójkowym oznacza:

1 x 2² = 4
0 x 2¹ = 0
1 x 2⁰ = 1

Wartość całej liczby to 4 + 0 + 1 = 5 w systemie dziesiętnym. Wydaje się to skomplikowane, ale komputery radzą sobie z tym doskonale!

Dlaczego to ważne? Bez systemu dwójkowego nie byłoby komputerów, smartfonów, internetu – niczego, co opiera się na cyfrowej technologii. To naprawdę podstawa wszystkiego!

Dlaczego Uczymy się o Różnych Systemach Liczbowych?

Możesz się zastanawiać: po co mi to wszystko? Po co mam się uczyć o systemach, których nie używam na co dzień?

Rozwija myślenie: Zrozumienie różnych systemów liczbowych pomaga rozwijać logiczne myślenie i zdolność rozwiązywania problemów.
Poszerza horyzonty: Pokazuje, że matematyka to nie tylko cyfry, których używamy na co dzień, ale także różne sposoby przedstawiania tych samych wartości.
Przygotowuje do przyszłości: W dzisiejszym świecie technologii, zrozumienie systemu dwójkowego jest bardzo przydatne, nawet jeśli nie zostaniesz programistą.

Cytat eksperta: "Matematyka to język wszechświata, a różne systemy liczbowe to różne dialekty tego języka." – powiedział kiedyś słynny matematyk. Chociaż nie pamiętam jego imienia, sens jest jasny: im więcej "dialektów" znasz, tym lepiej rozumiesz świat.

Praktyczne Wskazówki i Ćwiczenia

Oto kilka praktycznych wskazówek i ćwiczeń, które pomogą Ci lepiej zrozumieć systemy zapisywania liczb:

Ćwicz system rzymski: Napisz daty historyczne w systemie rzymskim. Spróbuj rozwiązywać proste działania matematyczne używając tych znaków.
Konwersja między systemami: Spróbuj zamieniać liczby dziesiętne na dwójkowe i odwrotnie. W internecie znajdziesz wiele kalkulatorów, które Ci w tym pomogą, ale spróbuj najpierw samodzielnie!
Zabawa z kodowaniem: Istnieją proste gry i aplikacje, które uczą podstaw kodowania i systemu dwójkowego w zabawny sposób. Poszukaj ich w internecie!

Przykład z życia: Kiedy piszesz SMS-a, Twój telefon zamienia litery na liczby w systemie dwójkowym, żeby przesłać wiadomość do innego telefonu. Fascynujące, prawda?

Dodatkowe Zasoby: Gdzie Szukać Więcej Informacji?

Jeśli chcesz dowiedzieć się więcej o systemach zapisywania liczb, polecam następujące źródła:

Książki i podręczniki: Sprawdź w swojej bibliotece podręczniki do matematyki dla starszych klas. Często zawierają rozdziały poświęcone różnym systemom liczbowym.
Strony internetowe: W internecie znajdziesz wiele stron poświęconych matematyce, które tłumaczą systemy liczbowe w prosty i przystępny sposób.
Filmy edukacyjne: Na YouTube znajdziesz wiele filmów, które wizualizują systemy liczbowe i pokazują, jak działają.

Pamiętaj: Nauka to proces. Nie zrażaj się, jeśli coś wydaje się trudne na początku. Ćwicz regularnie, a zobaczysz, że z czasem wszystko stanie się jasne!

Podsumowanie: Systemy Liczbowe to Klucz do Zrozumienia Świata

Poznanie różnych systemów zapisywania liczb to nie tylko nauka matematyki, ale także odkrywanie fascynującej historii i zrozumienie, jak działają komputery, które nas otaczają. Od starożytnych Rzymian, przez dzisiejsze komputery, liczby są podstawą naszego świata.

Zachęcam Cię do dalszego eksplorowania tego tematu. Eksperymentuj, zadawaj pytania, a przede wszystkim – baw się dobrze! Matematyka może być naprawdę fascynująca, jeśli tylko spojrzymy na nią z ciekawością.

Pamiętaj, że każdy wielki matematyk zaczynał od podstaw. Ty też możesz zostać mistrzem liczb! Powodzenia!