Systemy Zapisywania Liczb Klasa 4

Witajcie młodzi matematycy! Dzisiaj zagłębimy się w fascynujący świat systemów zapisywania liczb. Temat ten jest bardzo ważny, ponieważ zrozumienie różnych sposobów reprezentowania liczb jest podstawą do dalszej nauki matematyki. Skupimy się na systemach, które poznajecie już w 4 klasie szkoły podstawowej, ale spojrzymy na nie odrobinę głębiej, żebyście naprawdę zrozumieli, o co w nich chodzi.

System Dziesiętny – Nasz Codzienny System

System dziesiętny, nazywany też decymaльным, to system, którego używamy na co dzień. Dlaczego akurat dziesiętny? Ponieważ używa dziesięciu cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Wszystkie liczby, które znacie, są zapisywane właśnie w tym systemie.

Wartość Pozycyjna

Kluczem do zrozumienia systemu dziesiętnego jest pojęcie wartości pozycyjnej. Oznacza to, że wartość cyfry zależy od jej pozycji w liczbie. Przykładowo, w liczbie 345:

Cyfra 5 znajduje się na pozycji jedności (10⁰), więc reprezentuje 5 * 1 = 5.
Cyfra 4 znajduje się na pozycji dziesiątek (10¹), więc reprezentuje 4 * 10 = 40.
Cyfra 3 znajduje się na pozycji setek (10²), więc reprezentuje 3 * 100 = 300.

Dlatego liczba 345 to w rzeczywistości 300 + 40 + 5.

Wartość pozycyjna jest potęgą liczby 10. Idąc od prawej do lewej mamy kolejno: jedności (10⁰), dziesiątki (10¹), setki (10²), tysiące (10³), dziesiątki tysięcy (10⁴), setki tysięcy (10⁵), miliony (10⁶) i tak dalej.

Przykład: Rozłóżmy liczbę 78 219 na wartości pozycyjne:

9 na pozycji jedności: 9 * 1 = 9
1 na pozycji dziesiątek: 1 * 10 = 10
2 na pozycji setek: 2 * 100 = 200
8 na pozycji tysięcy: 8 * 1000 = 8 000
7 na pozycji dziesiątek tysięcy: 7 * 10 000 = 70 000

Czyli 78 219 = 70 000 + 8 000 + 200 + 10 + 9.

Dlaczego 10?

Dlaczego akurat 10? Prawdopodobnie dlatego, że ludzie od dawna używali palców u rąk do liczenia. Mamy 10 palców, więc system dziesiętny stał się dla nas naturalny.

System Rzymski – Starożytny System

System rzymski jest starszym systemem zapisywania liczb, który używany był w starożytnym Rzymie. Nadal spotykamy go na zegarach, w numeracji tomów książek, czy w oznaczeniach dat.

Symbole i Wartości

System rzymski używa liter do reprezentowania liczb. Najważniejsze symbole to:

I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000

Zasady Zapisywania Liczb

Zapisywanie liczb w systemie rzymskim opiera się na kilku zasadach:

Dodawanie: Jeśli symbol o mniejszej lub równej wartości znajduje się po prawej stronie symbolu o większej wartości, to ich wartości dodajemy. Na przykład: VI = 5 + 1 = 6, XI = 10 + 1 = 11.
Odejmowanie: Jeśli symbol o mniejszej wartości znajduje się po lewej stronie symbolu o większej wartości, to jego wartość odejmujemy od wartości większego symbolu. Na przykład: IV = 5 - 1 = 4, IX = 10 - 1 = 9.
Powtarzanie: Symbole I, X, C i M mogą być powtarzane maksymalnie trzy razy obok siebie. Na przykład: III = 3, XXX = 30, CCC = 300, MMM = 3000.
Ograniczenia: Symbole V, L i D nigdy nie są powtarzane ani używane do odejmowania.

Przykłady:

2 = II
4 = IV
9 = IX
14 = XIV (10 + 4)
40 = XL (50 - 10)
90 = XC (100 - 10)
400 = CD (500 - 100)
900 = CM (1000 - 100)
1984 = MCMLXXXIV (1000 + 900 + 80 + 4)

Zastosowania Systemu Rzymskiego

Jak już wspomnieliśmy, system rzymski wciąż jest używany, choć nie tak powszechnie jak system dziesiętny. Możemy go spotkać w:

Zegarach: Często na tarczach zegarów używa się cyfr rzymskich.
Numeracji tomów książek i rozdziałów: W książkach często tom, rozdział lub wstęp oznaczane są cyframi rzymskimi.
Oznaczeniach dat na pomnikach i budynkach: Na starych budynkach można spotkać datę budowy zapisaną w systemie rzymskim.
Imionach władców: Często po imieniu władcy dodaje się cyfrę rzymską, aby odróżnić go od innych władców o tym samym imieniu (np. Ludwik XIV).

Porównanie Systemów – Dziesiętny vs. Rzymski

System dziesiętny jest dużo bardziej praktyczny do wykonywania działań matematycznych niż system rzymski. Wyobraźcie sobie, jak trudno byłoby dodawać, odejmować, mnożyć lub dzielić liczby zapisane w systemie rzymskim! System dziesiętny, dzięki swojej wartości pozycyjnej, ułatwia nam wykonywanie tych operacji.

Z drugiej strony, system rzymski ma swoje walory estetyczne i historyczne. Dodaje elegancji i powagi różnym oznaczeniom. Poza tym, znajomość systemu rzymskiego pozwala nam odczytywać daty na zabytkowych budowlach i rozumieć oznaczenia w książkach.

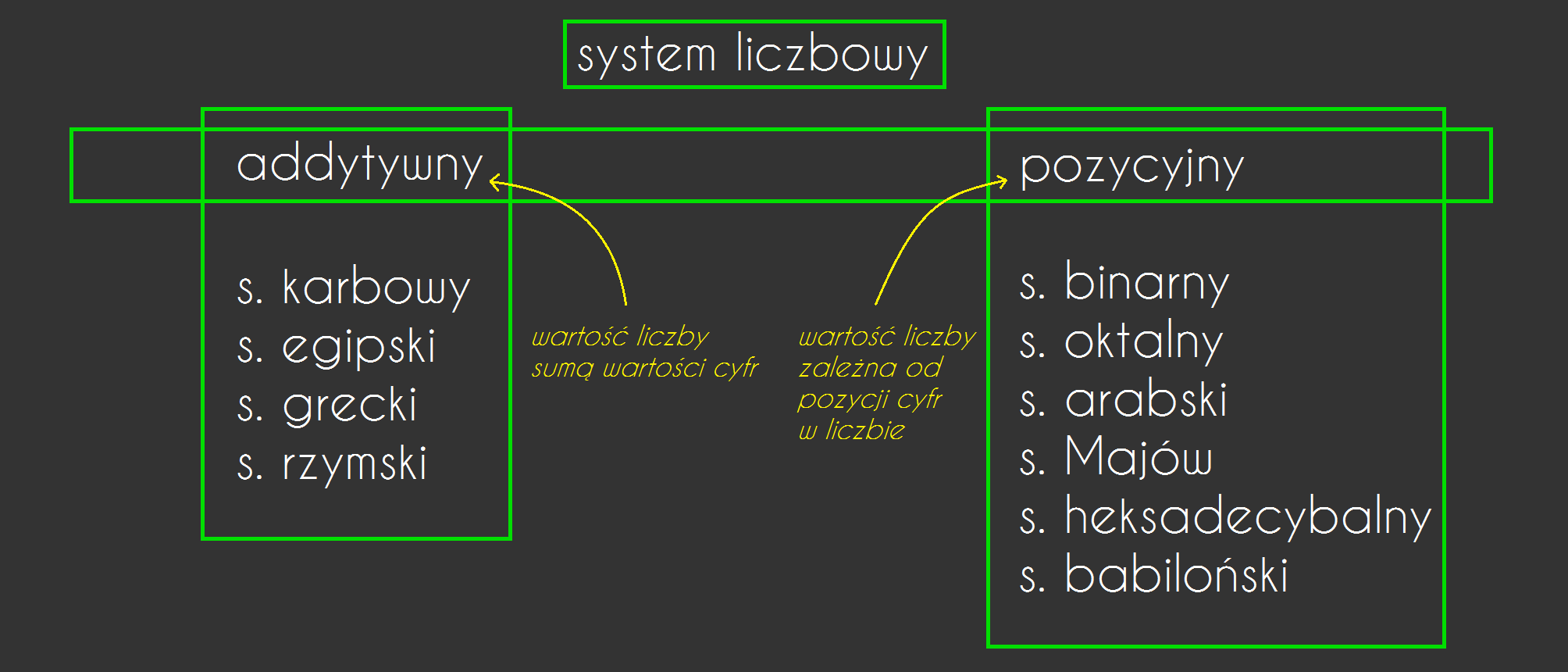
Systemy Pozycyjne – Uogólnienie

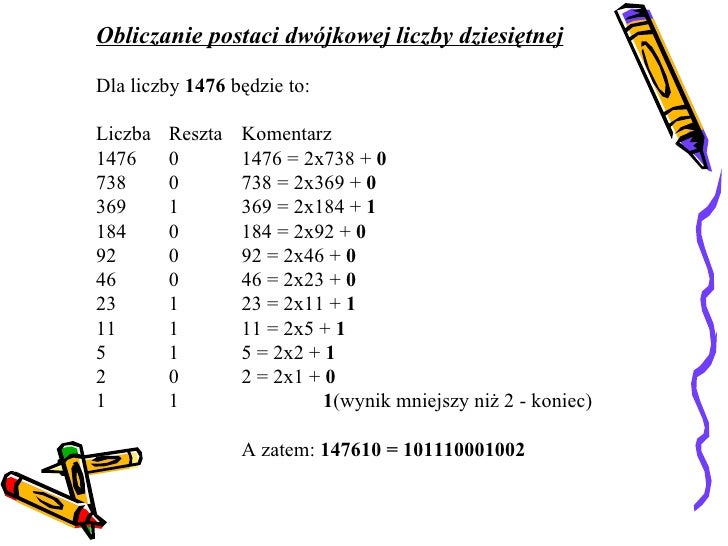
Zarówno system dziesiętny, jak i inne systemy, które moglibyście poznać w przyszłości (np. binarny - dwójkowy, ósemkowy, szesnastkowy), należą do rodziny systemów pozycyjnych. Charakteryzują się tym, że wartość cyfry zależy od jej pozycji w liczbie.

Każdy system pozycyjny ma swoją podstawę. W systemie dziesiętnym podstawą jest 10, co oznacza, że używamy 10 cyfr (0-9). System dwójkowy ma podstawę 2 (używa cyfr 0 i 1), system ósemkowy ma podstawę 8 (używa cyfr 0-7), a system szesnastkowy ma podstawę 16 (używa cyfr 0-9 i liter A-F, gdzie A=10, B=11, C=12, D=13, E=14, F=15).

Zrozumienie podstawy systemu pozwala nam przeliczać liczby z jednego systemu na inny. To zagadnienie wykracza poza program 4 klasy, ale warto o tym wiedzieć, żeby zrozumieć, że system dziesiętny to tylko jeden z wielu sposobów zapisywania liczb.

Przykłady z życia codziennego

Chociaż na co dzień operujemy głównie systemem dziesiętnym, warto zauważyć, gdzie jeszcze spotykamy inne systemy:

Komputery: Komputery działają na systemie dwójkowym (binarnym). Wszystkie informacje, od tekstów po zdjęcia i filmy, są zapisywane jako ciągi zer i jedynek.
Zegarki: Jak już wspomnieliśmy, tarcze niektórych zegarków wykorzystują cyfry rzymskie.
Numery domów: Czasami w numeracji domów używa się cyfr rzymskich dla oznaczenia klatek schodowych lub budynków w kompleksie.
Wiek: Czasami piszemy "XX wiek" lub "XXI wiek", używając cyfr rzymskich.

Podsumowanie

W tym artykule omówiliśmy dwa ważne systemy zapisywania liczb: system dziesiętny i system rzymski. Poznaliście wartość pozycyjną w systemie dziesiętnym oraz zasady zapisywania liczb w systemie rzymskim. Zobaczyliście również, gdzie te systemy są używane w życiu codziennym. Pamiętajcie, że zrozumienie systemów zapisywania liczb jest kluczowe dla dalszej nauki matematyki!

Ćwiczenie: Spróbujcie zamienić kilka liczb z systemu dziesiętnego na system rzymski i odwrotnie. Możecie poprosić rodziców lub nauczyciela o pomoc. Im więcej będziecie ćwiczyć, tym lepiej zrozumiecie te systemy!

Pamiętajcie, że matematyka to przygoda! Eksplorujcie, zadawajcie pytania i bawcie się liczbami!