Symetrie Sprawdzian Klasa 8 Gwo

Temat symetrii jest fundamentalny w matematyce i często pojawia się na sprawdzianach w ósmej klasie, szczególnie w szkołach korzystających z podręczników wydawnictwa GWO. Zrozumienie symetrii wymaga zarówno opanowania definicji, jak i umiejętności identyfikowania oraz tworzenia figur symetrycznych. Ten artykuł ma na celu kompleksowe omówienie tego zagadnienia, przygotowując uczniów do sprawdzianu i dając solidne podstawy do dalszej nauki.

Czym jest symetria?

Symetria, mówiąc najprościej, to harmonia i równowaga w układzie elementów. W matematyce rozróżniamy kilka rodzajów symetrii, z których najczęściej spotykane na sprawdzianach w ósmej klasie to:

Symetria osiowa

Symetria osiowa (zwana też odbiciem lustrzanym) występuje, gdy figura ma oś symetrii. Oś symetrii to linia, która dzieli figurę na dwie identyczne części, które są swoimi wzajemnymi odbiciami. Innymi słowy, gdybyśmy złożyli figurę wzdłuż osi symetrii, obie połówki idealnie by się pokryły.

Przykłady:

Litera "A" ma jedną oś symetrii (pionową).
Kwadrat ma cztery osie symetrii (dwie pionowe i poziome, oraz dwie po przekątnych).
Okrąg ma nieskończenie wiele osi symetrii (każda linia przechodząca przez środek okręgu jest osią symetrii).

Jak sprawdzić, czy figura ma oś symetrii? Można to zrobić wizualnie, próbując narysować linię, wzdłuż której figura wyglądałaby identycznie po obu stronach. Można też użyć lusterka – jeśli ustawimy lusterko wzdłuż potencjalnej osi symetrii i odbicie dopełnia figurę, to mamy do czynienia z osią symetrii.

Symetria środkowa

Symetria środkowa występuje, gdy figura ma środek symetrii. Środek symetrii to punkt, względem którego każdy punkt figury ma swój odpowiednik w równej odległości po przeciwnej stronie tego punktu. Wyobraźmy sobie, że obracamy figurę o 180 stopni wokół środka symetrii – jeśli figura wygląda identycznie jak przed obrotem, to ma środek symetrii.

Przykłady:

Litera "S" ma środek symetrii.
Równoległobok ma środek symetrii (punkt przecięcia przekątnych).
Okrąg ma środek symetrii (środek okręgu).

Jak sprawdzić, czy figura ma środek symetrii? Wyobraźmy sobie obrót figury o 180 stopni wokół potencjalnego środka. Jeśli po obrocie figura wygląda tak samo, to dany punkt jest środkiem symetrii.

Konstruowanie figur symetrycznych

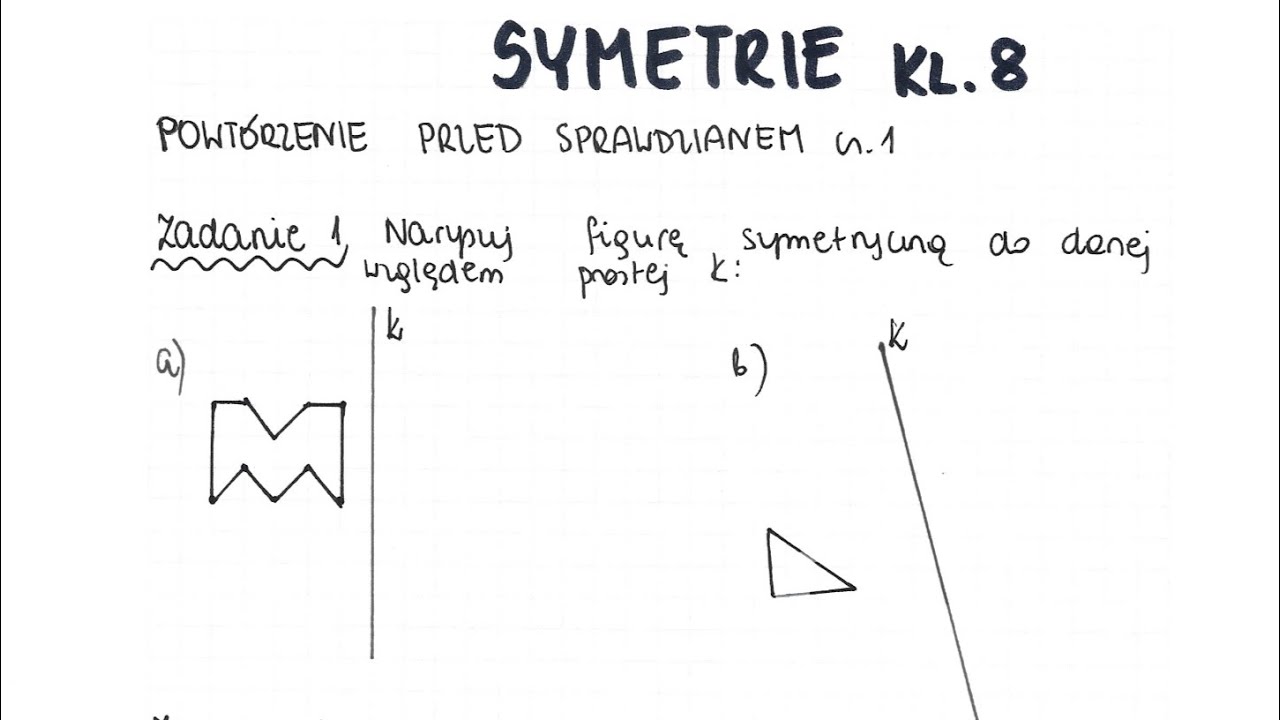
Kolejnym ważnym elementem sprawdzianu jest umiejętność konstruowania figur symetrycznych. Oznacza to, że na podstawie danej figury i osi (lub środka) symetrii, trzeba dorysować drugą część figury tak, aby całość była symetryczna.

Konstruowanie figury symetrycznej osiowo

Aby skonstruować figurę symetryczną osiowo, należy wykonać następujące kroki:

Wybierz charakterystyczne punkty na danej figurze (np. wierzchołki wielokąta).
Poprowadź proste prostopadłe do osi symetrii, przechodzące przez te punkty.
Odmierz odległość każdego punktu od osi symetrii.
Na prostej prostopadłej, po drugiej stronie osi symetrii, odmierz taką samą odległość. Otrzymasz punkt symetryczny do punktu początkowego.
Połącz wszystkie punkty symetryczne, aby uzyskać figurę symetryczną.

Ważne! Upewnij się, że odcinki łączące punkty symetryczne są odpowiednio długie i tworzą odpowiednie kąty.

Konstruowanie figury symetrycznej środkowo

Aby skonstruować figurę symetryczną środkowo, należy wykonać następujące kroki:

Wybierz charakterystyczne punkty na danej figurze.
Poprowadź proste przechodzące przez te punkty i środek symetrii.
Odmierz odległość każdego punktu od środka symetrii.
Na prostej przechodzącej przez punkt i środek symetrii, po drugiej stronie środka, odmierz taką samą odległość. Otrzymasz punkt symetryczny do punktu początkowego.
Połącz wszystkie punkty symetryczne, aby uzyskać figurę symetryczną.

Ważne! Pamiętaj, że punkty symetryczne środkowo leżą na jednej prostej przechodzącej przez środek symetrii.

Symetria w życiu codziennym i w geometrii

Symetria jest wszechobecna w naszym otoczeniu. Znajdziemy ją w architekturze (np. fasady budynków), w naturze (np. motyle, płatki śniegu), w sztuce i w designie. Zrozumienie symetrii pozwala nam lepiej doceniać piękno i harmonię otaczającego nas świata.

W geometrii symetria jest kluczowym elementem wielu definicji i twierdzeń. Na przykład, trapez równoramienny jest trapezem, który ma oś symetrii przechodzącą przez środki jego podstaw. Deltoid jest czworokątem, który ma jedną oś symetrii, która jest jednocześnie przekątną.

Znajomość symetrii ułatwia rozwiązywanie zadań geometrycznych. Na przykład, jeśli wiemy, że figura jest symetryczna osiowo, to możemy wykorzystać tę informację do obliczenia długości odcinków, miar kątów lub pola powierzchni.

Przykładowe zadania ze sprawdzianu (GWO)

Na sprawdzianie z symetrii (opartego na programie GWO) możesz spodziewać się następujących typów zadań:

Identyfikacja osi i środków symetrii: Dany jest zbiór figur, a Twoim zadaniem jest wskazanie, które z nich mają osie symetrii, które mają środki symetrii, a które nie mają żadnego z nich.
Konstruowanie figur symetrycznych: Dany jest fragment figury i oś/środek symetrii, a Twoim zadaniem jest dorysowanie brakującej części figury, tak aby całość była symetryczna.
Zadania tekstowe z wykorzystaniem symetrii: Na przykład, "Dany jest trójkąt równoramienny o podstawie długości 10 cm i ramieniu długości 13 cm. Oblicz wysokość trójkąta opuszczoną na podstawę." W tym zadaniu należy wykorzystać fakt, że wysokość opuszczona na podstawę w trójkącie równoramiennym jest jednocześnie osią symetrii tego trójkąta.
Zadania praktyczne: Na przykład, "Znajdź wszystkie osie symetrii w danym logo firmy."

Przykład zadania: Narysuj figurę symetryczną do kwadratu ABCD względem prostej k, która jest równoległa do boku AB i znajduje się w odległości 2 cm od tego boku. Bok kwadratu ma długość 5 cm. Oblicz pole otrzymanej figury.

Rozwiązanie: Najpierw rysujemy kwadrat ABCD. Następnie rysujemy prostą k równoległą do boku AB w odległości 2 cm od niego. Konstruujemy punkty symetryczne do punktów A, B, C i D względem prostej k. Otrzymujemy kwadrat A'B'C'D', który jest symetryczny do kwadratu ABCD. Cała figura składa się z dwóch kwadratów i prostokąta pomiędzy nimi. Pole każdego kwadratu wynosi 5cm * 5cm = 25 cm². Wysokość prostokąta wynosi 4 cm (2 cm + 2 cm), a szerokość wynosi 5 cm. Zatem pole prostokąta wynosi 4 cm * 5 cm = 20 cm². Pole całej figury wynosi 25 cm² + 25 cm² + 20 cm² = 70 cm².

Wskazówki na sprawdzian

Oto kilka przydatnych wskazówek, które pomogą Ci dobrze napisać sprawdzian z symetrii:

Dokładnie czytaj polecenia: Upewnij się, że rozumiesz, co dokładnie masz zrobić w danym zadaniu.
Używaj przyborów geometrycznych: Do rysowania figur symetrycznych używaj linijki, kątomierza i cyrkla. To zapewni dokładność i precyzję.
Sprawdzaj swoje rozwiązania: Po wykonaniu zadania, sprawdź, czy Twoja figura jest rzeczywiście symetryczna. Możesz to zrobić wizualnie lub za pomocą lusterka.
Ćwicz, ćwicz i jeszcze raz ćwicz: Rozwiąż jak najwięcej zadań z podręcznika, zbioru zadań i arkuszy egzaminacyjnych. Im więcej ćwiczysz, tym lepiej zrozumiesz zasady symetrii i szybciej będziesz rozwiązywać zadania.
Zrozum koncepcje, a nie tylko zapamiętuj: Staraj się zrozumieć, dlaczego dana figura jest symetryczna, a nie tylko zapamiętywać definicje na pamięć. To pomoże Ci rozwiązywać zadania nietypowe i wymagające myślenia.

Pamiętaj! Symetria to piękna i fascynująca dziedzina matematyki. Zrozumienie zasad symetrii nie tylko pomoże Ci dobrze napisać sprawdzian, ale także rozwinie Twoje umiejętności logicznego myślenia i rozwiązywania problemów.

Podsumowanie

Symetria jest kluczowym zagadnieniem w matematyce, a jej zrozumienie jest niezbędne do pomyślnego zdania sprawdzianu w ósmej klasie. Pamiętaj o rozróżnianiu symetrii osiowej i środkowej, o umiejętności konstruowania figur symetrycznych i o wykorzystywaniu symetrii do rozwiązywania zadań geometrycznych. Przeczytaj uważnie ten artykuł, rozwiąż przykładowe zadania i zastosuj się do wskazówek, a na pewno poradzisz sobie na sprawdzianie!

Powodzenia na sprawdzianie z symetrii! Ćwicz regularnie, a sukces jest gwarantowany!