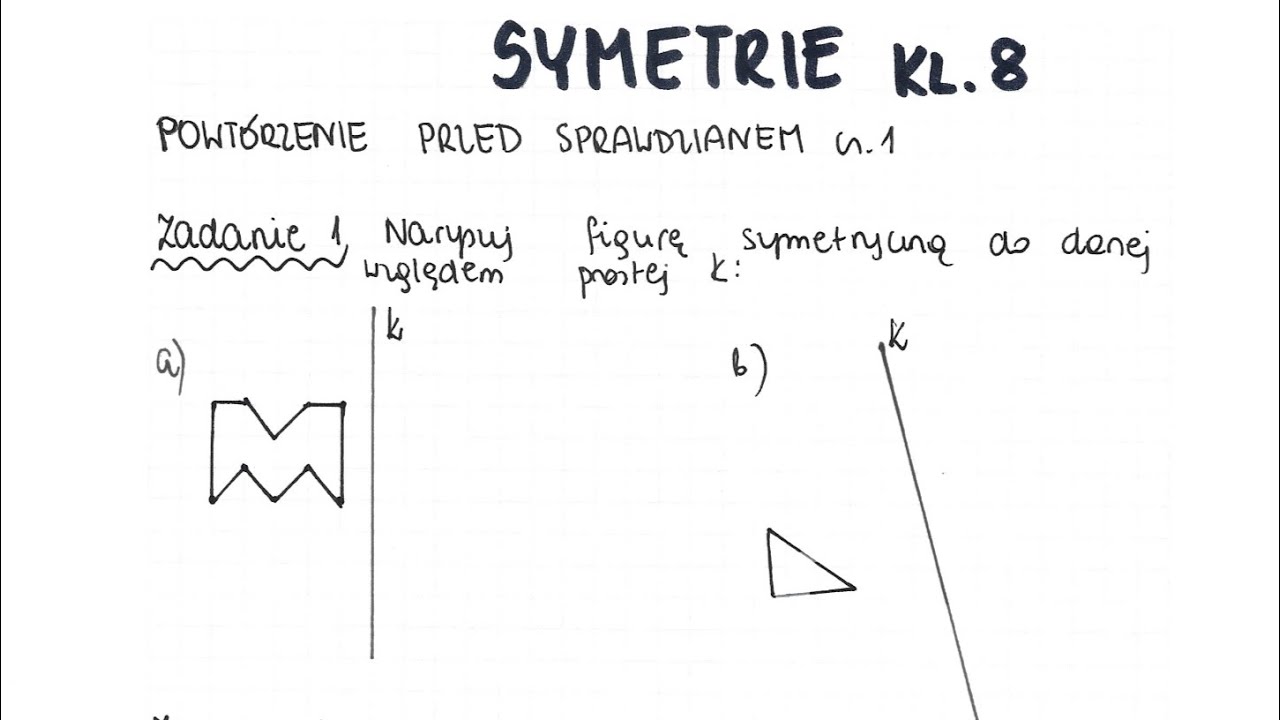
Symetrie Sprawdzian Kl 3 Podstawowa Geometria

Witaj! Ten przewodnik pomoże Ci zrozumieć symetrię, temat, który często pojawia się w geometrii w 3 klasie szkoły podstawowej. Zaczniemy od samej definicji i krok po kroku wyjaśnimy najważniejsze kwestie.
Co to jest symetria?
Najprościej mówiąc, symetria to cecha, która sprawia, że coś wygląda identycznie po odbiciu lub obróceniu. Wyobraź sobie, że masz obrazek i możesz go złożyć na pół tak, że obie połowy idealnie się pokrywają. Wtedy mówimy, że ten obrazek jest symetryczny.
Rodzaje symetrii
Istnieją różne rodzaje symetrii, ale na początek skupimy się na najważniejszym: symetrii osiowej, nazywanej też symetrią względem prostej.
Symetria osiowa (względem prostej): Wyobraź sobie, że masz figurę i prostą (linię prostą). Ta prosta działa jak lustro. Każdy punkt figury ma swój "odpowiednik" po drugiej stronie lustra, w tej samej odległości od prostej. Ta prosta, "lustro", nazywana jest osią symetrii.
Przykład: Liść! Większość liści ma oś symetrii biegnącą przez środek. Jeśli narysowalibyśmy tę linię, to prawa i lewa strona liścia byłyby niemal identyczne (odbicie lustrzane jednej strony na drugą).
Jak rozpoznać symetrię osiową?
Aby stwierdzić, czy figura ma oś symetrii, możesz spróbować wykonać kilka rzeczy:
- Wyobraź sobie: Czy możesz narysować linię przez figurę tak, żeby po obu jej stronach powstały identyczne "odbicia"?
- Złóż papier: Narysuj figurę na kartce papieru. Spróbuj złożyć kartkę wzdłuż linii, którą uważasz za oś symetrii. Jeśli obie połówki figury idealnie się pokrywają, to znaczy, że znalazłeś oś symetrii.
- Użyj lusterka: Postaw lusterko na domniemanej osi symetrii. Czy to, co widzisz w lusterku, uzupełnia figurę tak, że wygląda na kompletną?
Przykłady: * Kwadrat: Ma 4 osie symetrii. Można go złożyć na pół pionowo, poziomo i po obu przekątnych. * Prostokąt: Ma 2 osie symetrii. Można go złożyć na pół pionowo i poziomo. * Koło: Ma nieskończenie wiele osi symetrii! Każdą linię przechodzącą przez środek koła można uznać za oś symetrii. * Trójkąt równoboczny: Ma 3 osie symetrii. * Litera A: Ma jedną oś symetrii pionową.
Gdzie spotykamy symetrię na co dzień?
Symetria jest wszędzie wokół nas!
- W architekturze: Wiele budynków jest symetrycznych, ponieważ wygląda to estetycznie.
- W naturze: Motyle, liście, kwiaty – wiele elementów natury charakteryzuje się symetrią.
- W sztuce: Artyści często wykorzystują symetrię w swoich dziełach, aby stworzyć harmonię i równowagę.
- W życiu codziennym: Nasze twarze są w przybliżeniu symetryczne (chociaż nie idealnie!). Ubrania, meble, a nawet samochody często projektowane są z uwzględnieniem symetrii.
Zwróć uwagę na otoczenie! Z pewnością znajdziesz wiele przykładów symetrii osiowej. To naprawdę fajny temat, który pozwala lepiej zrozumieć świat wokół nas. Powodzenia na sprawdzianie!