Symetria Względem Punktu 0 0

Zmagasz się z geometrii? Czujesz, że pojęcia takie jak symetria są trudne do ogarnięcia? Nie martw się, nie jesteś sam! Wielu uczniów, a nawet dorosłych, ma problem z wizualizacją i zrozumieniem symetrii, a zwłaszcza symetrii względem punktu (0,0), czyli środka układu współrzędnych. Ten artykuł ma na celu to zmienić. Bez zbędnego żargonu, krok po kroku, wyjaśnimy, czym jest symetria względem punktu (0,0), jak ją rozpoznawać i jak z niej korzystać.

Czym jest symetria względem punktu (0,0)?

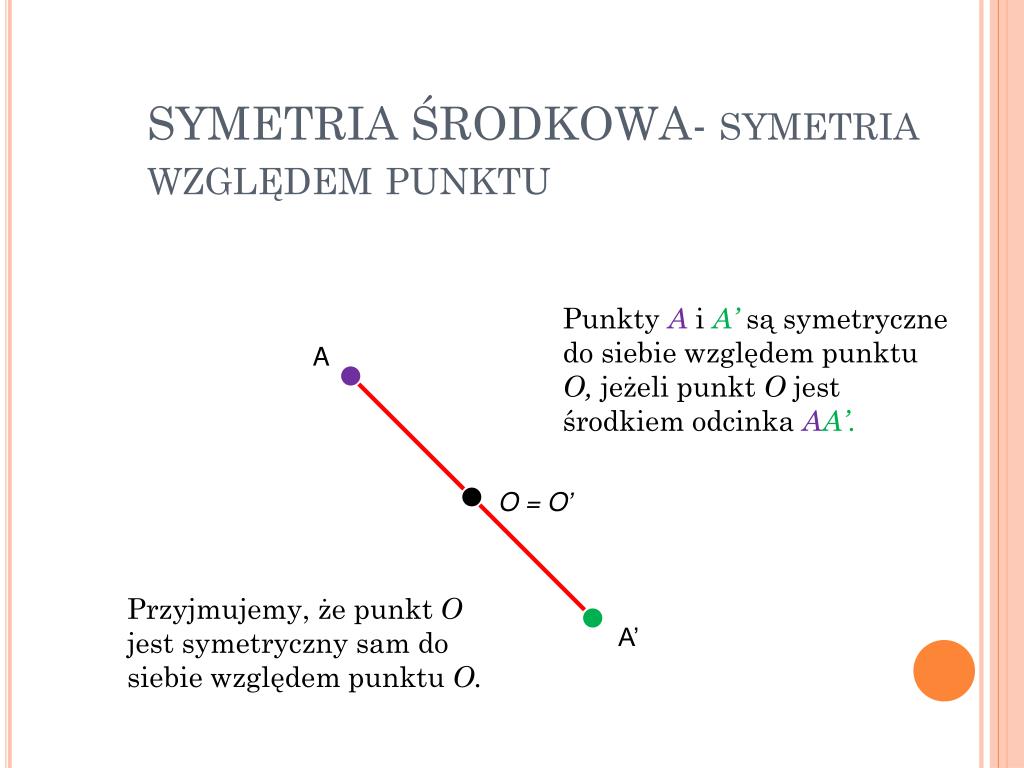
Wyobraź sobie kartkę papieru. Narysuj na niej dowolną figurę. Teraz wyobraź sobie, że masz pinezkę wbijtą w środku tej kartki, dokładnie w punkcie (0,0). Obróć kartkę o 180 stopni. Jeśli figura wygląda *dokładnie* tak samo jak przed obrotem, to znaczy, że jest symetryczna względem punktu (0,0). To najprostsze wyjaśnienie.

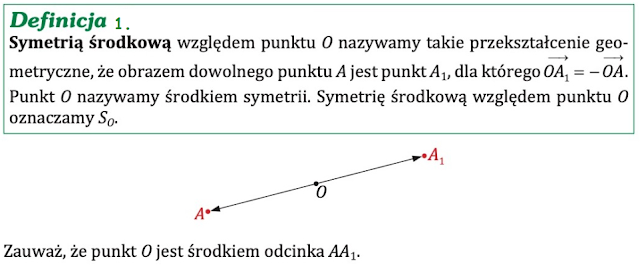
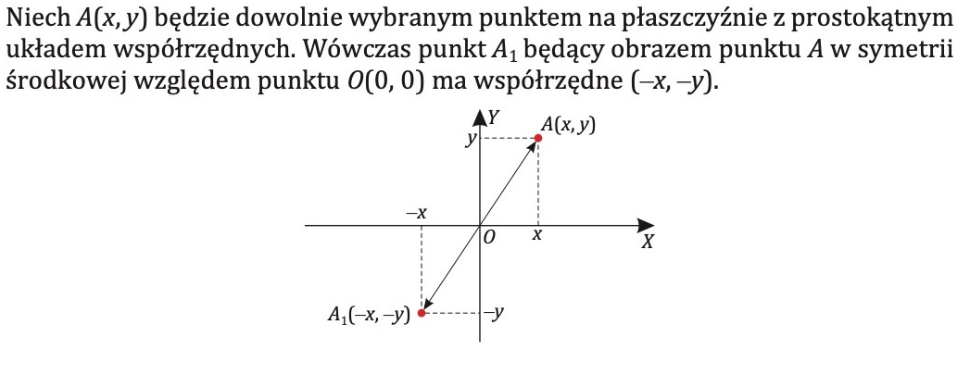
Bardziej formalnie, symetria względem punktu (0,0) (nazywana również symetrią środkową) oznacza, że dla każdego punktu *P* o współrzędnych (x, y), znajdującego się na danej figurze, istnieje punkt *P'* o współrzędnych (-x, -y), który również leży na tej figurze. Punkt *P'* jest obrazem punktu *P* w symetrii względem punktu (0,0).

Brzmi trochę skomplikowanie? Spróbujmy to uprościć. Weźmy punkt (2, 3). Jego obraz w symetrii względem (0,0) to punkt (-2, -3). Zmieniłeś znak każdej współrzędnej. I to wszystko! Ta prosta zmiana znaku jest kluczem do zrozumienia symetrii względem środka układu współrzędnych.

Jak rozpoznać figurę symetryczną względem (0,0)?

Oto kilka praktycznych wskazówek, które pomogą Ci zidentyfikować figury symetryczne względem punktu (0,0):

Wyobraź sobie obrót o 180 stopni: To najprostsza i często najskuteczniejsza metoda. Jeśli figura wygląda identycznie po obrocie o pół obrotu wokół punktu (0,0), to jest symetryczna.
Sprawdź pary punktów: Wybierz kilka punktów na figurze. Znajdź ich "odpowiedniki" - punkty o przeciwnych współrzędnych. Jeśli wszystkie te "odpowiedniki" leżą na figurze, to figura jest symetryczna.
Zwróć uwagę na typowe figury: Niektóre figury są z natury symetryczne względem (0,0). Należą do nich np. okręgi, których środek znajduje się w punkcie (0,0), hiperbole o środku w (0,0) i niektóre wielokąty foremne (np. sześciokąt foremny o środku w (0,0)).
Linie proste przechodzące przez (0,0): Każda linia prosta przechodząca przez punkt (0,0) jest symetryczna względem tego punktu.

Przykład: Rozważmy prostą o równaniu y = x. Weźmy punkt (1, 1) na tej prostej. Jego obraz w symetrii względem (0,0) to punkt (-1, -1). Czy punkt (-1, -1) leży na prostej y = x? Tak, bo -1 = -1. Możemy sprawdzić to dla wielu punktów i zawsze się to potwierdzi. Zatem prosta y = x jest symetryczna względem punktu (0,0).

Przykłady figur symetrycznych względem (0,0) i tych, które nie są

Figury symetryczne względem (0,0):

Okrąg o środku w (0,0): Niezależnie od promienia.
Hiperbola o równaniu xy = k: Gdzie k jest dowolną liczbą różną od zera.
Funkcja y = x³: Podstawienie -x daje y = (-x)³ = -x³, co pokazuje symetrię.
Niektóre wielokąty foremne: Takie jak sześciokąt foremny o środku w (0,0).
Linia prosta przechodząca przez (0,0): Np. y = 2x, y = -x/3.

Figury nie symetryczne względem (0,0):

Kwadrat, którego środek nie znajduje się w (0,0): Przesunięcie figury zaburza symetrię.
Parabola y = x²: Zauważ, że punkt (1, 1) leży na paraboli, ale punkt (-1, -1) już nie.
Linia prosta, która *nie* przechodzi przez (0,0): Np. y = x + 1.
Trójkąt: Trójkąty generalnie nie są symetryczne względem (0,0), chyba że są bardzo specyficzne i ich środek "pokrywa się" z punktem (0,0) a ich kształt to umożliwia.

Praktyczne zastosowania symetrii względem (0,0)

Symetria względem punktu (0,0) nie jest tylko abstrakcyjnym pojęciem matematycznym. Ma wiele praktycznych zastosowań, m.in.:

Grafika komputerowa: Wykorzystywana do tworzenia symetrycznych wzorów, obiektów i animacji.
Fizyka: Prawa fizyki często wykazują symetrię, co upraszcza obliczenia i analizy. Np. symetria w rozkładzie ładunków elektrycznych.
Kryptografia: Symetria może być wykorzystywana do tworzenia algorytmów szyfrujących.
Architektura i projektowanie: Symetria jest ważnym elementem estetycznym w budynkach i przedmiotach użytkowych.
Matematyka: Pomaga w rozwiązywaniu równań i problemów geometrycznych. Zauważenie symetrii może znacząco uprościć zadanie.

Przykład z życia wzięty: Pomyśl o logo swojej ulubionej marki. Wiele logotypów jest celowo projektowanych tak, aby były symetryczne (względem osi, punktu lub obu), ponieważ symetria jest postrzegana jako przyjemna dla oka i budzi zaufanie. Sprawdź to sam!

Jak ćwiczyć i utrwalać wiedzę o symetrii względem (0,0)?

Najlepszym sposobem na opanowanie symetrii względem punktu (0,0) jest praktyka! Oto kilka propozycji:

Rysuj figury i ich obrazy w symetrii względem (0,0): Zacznij od prostych figur, takich jak odcinki, trójkąty i kwadraty, a następnie przejdź do bardziej skomplikowanych kształtów.
Rozwiązuj zadania: W Internecie znajdziesz wiele zadań dotyczących symetrii. Spróbuj je rozwiązać.
Użyj programów do geometrii: Programy takie jak GeoGebra pozwalają na wizualizację symetrii i eksperymentowanie z różnymi figurami.
Analizuj otoczenie: Poszukaj przykładów symetrii w otaczającym Cię świecie. Zwróć uwagę na architekturę, wzory na ubraniach, logo firm.
Gry edukacyjne: Istnieją gry, które w zabawny sposób uczą o symetrii.

Podsumowanie

Symetria względem punktu (0,0) może wydawać się trudna, ale w rzeczywistości jest to proste pojęcie, które można łatwo zrozumieć i zastosować. Pamiętaj o kluczowej zasadzie: zmień znak każdej współrzędnej. Praktyka czyni mistrza, więc ćwicz i eksperymentuj, a symetria względem punktu (0,0) przestanie być dla Ciebie zagadką!

Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć to ważne pojęcie geometryczne. Pamiętaj, że nauka matematyki to proces, a każdy krok, nawet ten najmniejszy, przybliża Cię do celu. Powodzenia!