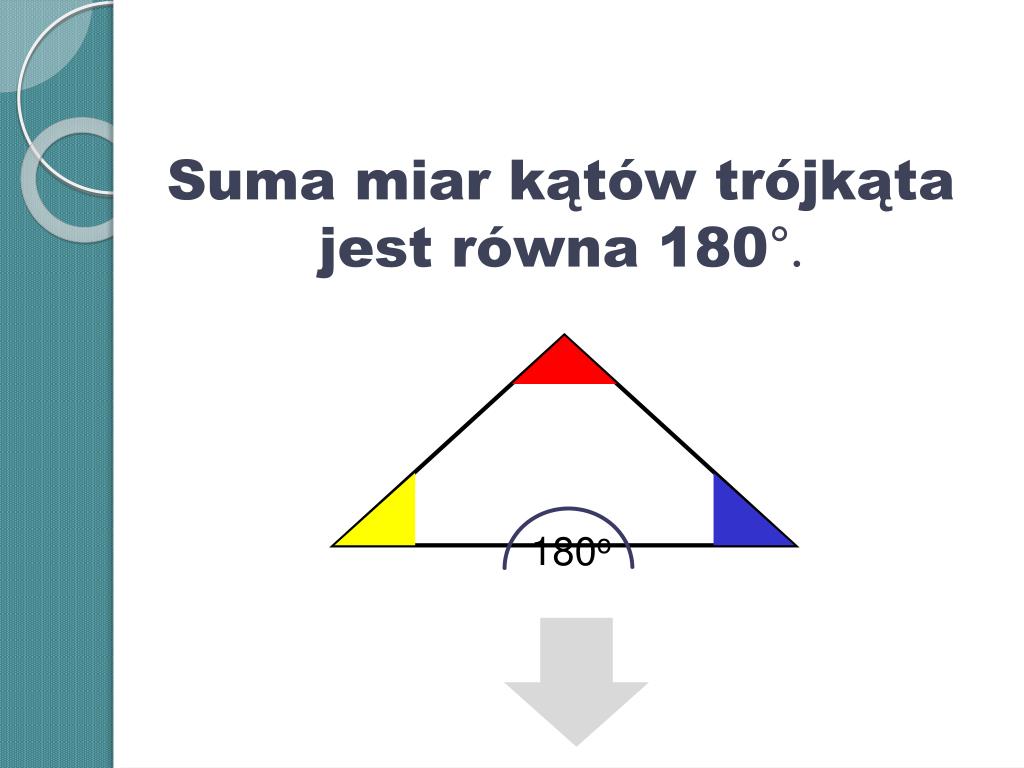
Suma Miar Kątów W Trójkącie Wynosi

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre konstrukcje stoją stabilnie przez setki lat, a inne zawalają się po kilku? Często odpowiedź kryje się w fundamentach, a w geometrii tym fundamentem jest właśnie zasada, że suma miar kątów w trójkącie wynosi 180 stopni. Może to brzmi jak sucha teoria, ale obiecuję, że to fascynująca i niezwykle użyteczna informacja!

Pomyśl o tym: budujesz dom, projektujesz most, a nawet rysujesz prosty plan pokoju – wszędzie tam, gdzie pojawiają się trójkąty, ta zasada jest absolutnie kluczowa. Brak jej zrozumienia może prowadzić do poważnych błędów i problemów. Zamiast straszyć, spróbujmy to zrozumieć i zobaczyć, jak możemy to wykorzystać w praktyce.

Dlaczego to w ogóle działa? Dowód, który ma sens.

Zrozumienie "dlaczego" jest tak samo ważne, jak samo zapamiętanie faktu. Istnieje prosty dowód, który sprawia, że suma miar kątów w trójkącie staje się czymś oczywistym, a nie tylko wyuczonym wzorem.

Wyobraź sobie trójkąt narysowany na kartce papieru. Narysuj prostą równoległą do jednego z boków trójkąta, przechodzącą przez wierzchołek przeciwległy temu bokowi. Teraz, wykorzystując właściwości kątów naprzemianległych i odpowiadających (kąty te są równe), zobaczysz, że trzy kąty trójkąta "wpasowują się" w linię prostą. A wiemy przecież, że kąt na linii prostej ma miarę 180 stopni! Proste, prawda?

Alternatywnie, możesz pomyśleć o obracaniu kartką. Zaczynasz w jednym wierzchołku, obracasz kartką wokół każdego z wierzchołków, aż wrócisz do punktu wyjścia. Suma kątów obrotu da Ci pełny obrót wokół punktu, czyli 360 stopni. Ponieważ wykonujesz obrót wokół każdego wierzchołka "na zewnątrz" trójkąta, suma zewnętrznych kątów trójkąta wynosi 360 stopni. Zewnętrzny kąt trójkąta plus jego odpowiadający mu wewnętrzny kąt daje 180 stopni. Masz trzy takie pary, więc 3 * 180 = 540. Odejmując od tego sumę kątów zewnętrznych (360), otrzymujesz sumę kątów wewnętrznych: 540 - 360 = 180 stopni.

Realny świat: Jak to wpływa na Twoje życie?

Ok, teoria za nami. Ale jak to się przekłada na realne życie? Otóż, wszędzie tam, gdzie projektowanie i konstrukcja opierają się na dokładności i stabilności, ta zasada odgrywa kluczową rolę.

Architektura i Inżynieria

Projektanci budynków i mostów muszą dokładnie obliczać kąty, aby zapewnić stabilność konstrukcji. Trójkąty są niezwykle mocne, dlatego często wykorzystuje się je w kratownicach i innych elementach nośnych. Jeśli suma kątów w trójkącie w projekcie kratownicy nie wynosi 180 stopni, konstrukcja nie będzie stabilna i może się zawalić.

Nawigacja i Geodezja

Żeglarze i geodeci od wieków korzystają z triangulacji – techniki, która opiera się na tworzeniu trójkątów i mierzeniu ich kątów, aby określić odległości i pozycje. To, co zaczęło się od prostych narzędzi, ewoluowało do zaawansowanych systemów GPS, ale zasada pozostała ta sama: suma kątów w trójkącie to podstawa.

Gry komputerowe i Grafika 3D

Nawet wirtualne światy gier komputerowych opierają się na matematyce! Obiekty 3D są często modelowane przy użyciu siatek trójkątów. Prawidłowe obliczenia kątów w tych trójkątach zapewniają, że obiekty wyglądają realistycznie i zachowują poprawne proporcje.

Przeciwnicy i kontrargumenty: A co z geometriami nieeuklidesowymi?

Oczywiście, zawsze znajdą się wyjątki od reguły. W geometriach nieeuklidesowych, takich jak geometria sferyczna (używana na powierzchni kuli ziemskiej), suma kątów w trójkącie *nie* zawsze wynosi 180 stopni. Może być większa! Dlaczego? Bo powierzchnia jest zakrzywiona.

Jednak w większości praktycznych zastosowań, z którymi spotykamy się na co dzień, pracujemy w przestrzeni euklidesowej, gdzie ta zasada jest niezmienna. Warto o tym pamiętać, ale nie ma potrzeby, aby to nas zniechęcało do zgłębiania tematu.

Jak wykorzystać tę wiedzę? Konkretne kroki.

Zamiast pozostawiać Cię z suchymi faktami, podzielę się kilkoma pomysłami na to, jak możesz aktywnie wykorzystać tę wiedzę:

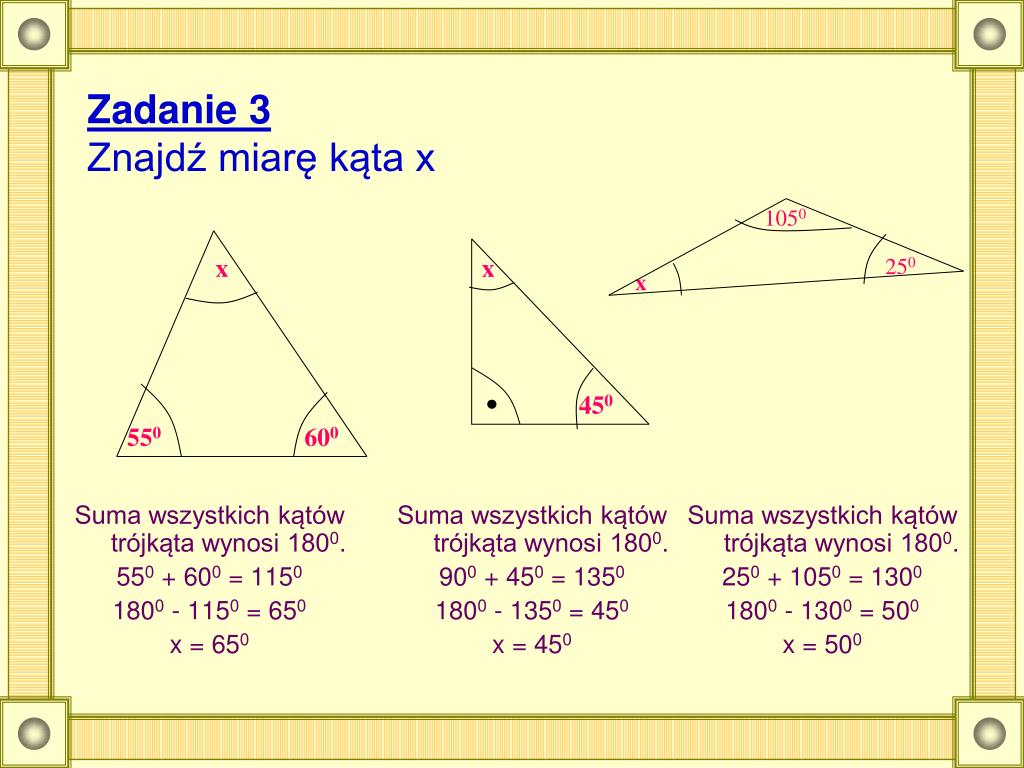
• Rozwiązywanie zadań z geometrii: To oczywiste, ale regularne rozwiązywanie zadań pomaga utrwalić wiedzę i nauczyć się stosować ją w praktyce.
• Obserwacja otoczenia: Zwracaj uwagę na trójkąty w architekturze, projektach mebli, a nawet w naturze. Spróbuj oszacować kąty i sprawdzić, czy suma rzeczywiście wynosi około 180 stopni.
• Eksperymenty: Narysuj trójkąt na kartce, zmierz jego kąty i zsumuj je. Powtórz to z różnymi rodzajami trójkątów (równoboczne, równoramienne, prostokątne).
• Programowanie: Jeśli znasz podstawy programowania, spróbuj napisać program, który oblicza trzeci kąt trójkąta na podstawie dwóch podanych kątów.

Przykłady z życia:

Budowa dachu:

Kąty nachylenia dachu muszą być precyzyjnie obliczone, aby zapewnić odprowadzanie wody i stabilność konstrukcji. Architekci wykorzystują zasadę sumy kątów w trójkącie do określenia optymalnego kąta nachylenia.

Projektowanie mebli:

Wiele mebli, zwłaszcza krzesła i stoły, wykorzystuje trójkątne wzmocnienia, aby zwiększyć ich wytrzymałość. Projektanci muszą uwzględnić kąty tych wzmocnień, aby zapewnić stabilność i uniknąć kołysania się mebla.

Nawigacja lotnicza:

Piloci wykorzystują triangulację i zasadę sumy kątów w trójkącie do określania swojej pozycji na podstawie sygnałów radiowych z różnych nadajników. To pozwala im na precyzyjne nawigowanie i unikanie przeszkód.

Podsumowanie i refleksja

Zasada, że suma miar kątów w trójkącie wynosi 180 stopni, to fundament geometrii i ma ogromny wpływ na wiele dziedzin naszego życia. Od architektury i inżynierii, przez nawigację, aż po gry komputerowe – wszędzie tam, gdzie liczy się precyzja i stabilność, ta zasada odgrywa kluczową rolę.

Pamiętaj, że zrozumienie "dlaczego" jest tak samo ważne, jak samo zapamiętanie faktu. Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć tę zasadę i zainspirował do dalszego zgłębiania tajników geometrii. Spróbuj sam zastosować tę wiedzę w praktyce. Zobaczysz, że matematyka może być fascynująca!

Czy po przeczytaniu tego artykułu dostrzegasz trójkąty i kąty w swoim otoczeniu inaczej niż wcześniej? Jak zamierzasz wykorzystać tę wiedzę w przyszłości?