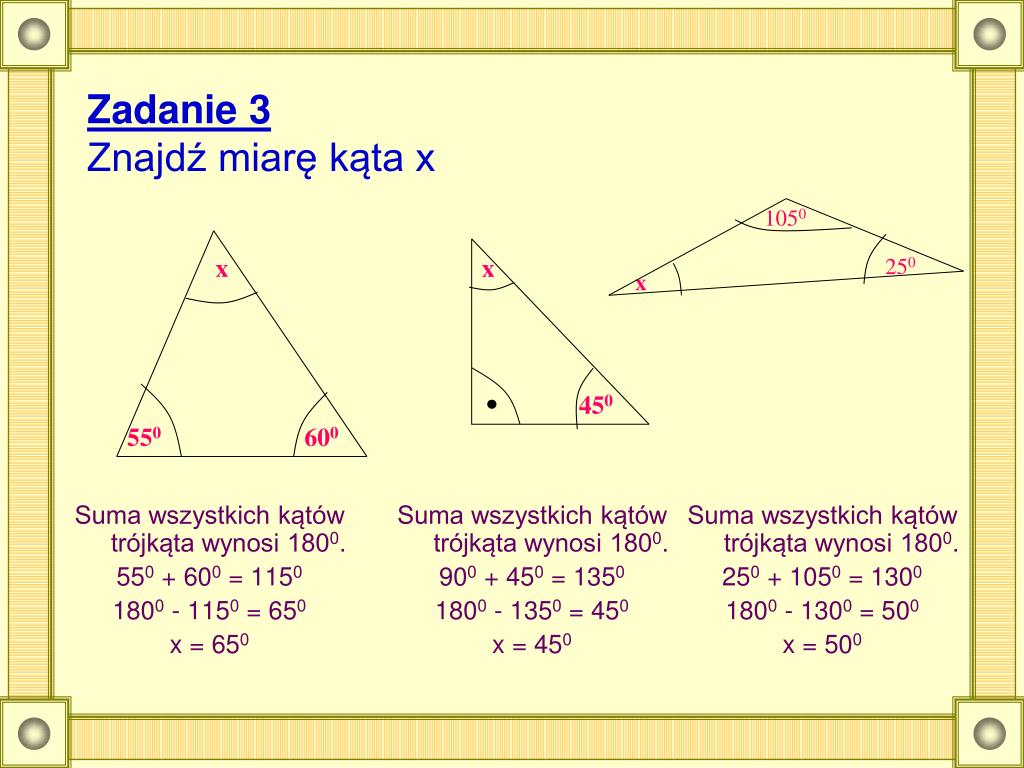
Suma Miar Kątów W Trójkącie

W geometrii euklidesowej, jedna z najbardziej fundamentalnych i intuicyjnych prawd dotyczy trójkątów: suma miar kątów wewnętrznych w każdym trójkącie wynosi zawsze 180 stopni. Ta prosta zasada, choć łatwa do zapamiętania, ma ogromne konsekwencje i jest podstawą dla wielu innych twierdzeń i obliczeń w geometrii i trygonometrii. W tym artykule zgłębimy tę fundamentalną własność trójkątów, analizując jej znaczenie, dowody i zastosowania.
Kluczowe punkty i argumenty
Podstawowe definicje i pojęcia
Zanim przejdziemy dalej, upewnijmy się, że rozumiemy podstawowe pojęcia. Trójkąt to figura geometryczna utworzona przez trzy odcinki łączące trzy punkty, które nie leżą na jednej prostej. Kąt wewnętrzny trójkąta to kąt utworzony przez dwa boki trójkąta wewnątrz figury. Mówiąc o "sumie miar kątów", mamy na myśli dodanie miar (zazwyczaj wyrażonych w stopniach) każdego z trzech kątów wewnętrznych trójkąta.
Stopień jest jednostką miary kąta, gdzie pełny obrót odpowiada 360 stopniom. Kąt prosty ma miarę 90 stopni, a kąt półpełny 180 stopni. Zrozumienie tych podstawowych pojęć jest kluczowe do zrozumienia istoty twierdzenia o sumie kątów w trójkącie.
Dowód twierdzenia o sumie kątów w trójkącie
Istnieje kilka sposobów, aby udowodnić, że suma miar kątów w trójkącie wynosi 180 stopni. Jeden z najczęściej stosowanych i intuicyjnych dowodów opiera się na własnościach linii równoległych.
Wyobraźmy sobie dowolny trójkąt ABC. Przez wierzchołek A prowadzimy prostą równoległą do boku BC. Teraz, na tej prostej, kąty utworzone przy wierzchołku A są naprzemianległe wewnętrzne do kątów przy wierzchołkach B i C trójkąta ABC. Oznacza to, że miara kąta przy wierzchołku B jest równa mierze kąta naprzemianległego przy wierzchołku A (nazwijmy go kątem B'), a miara kąta przy wierzchołku C jest równa mierze kąta naprzemianległego przy wierzchołku A (nazwijmy go kątem C').
Kąty A, B' i C' tworzą razem kąt półpełny, czyli kąt o mierze 180 stopni. Ponieważ B' = B i C' = C, wynika z tego, że A + B + C = 180 stopni. To właśnie dowodzi, że suma miar kątów wewnętrznych w trójkącie ABC wynosi 180 stopni.
Konsekwencje i implikacje
Twierdzenie o sumie kątów w trójkącie ma wiele ważnych konsekwencji:
* Znając dwie miary kątów w trójkącie, możemy zawsze obliczyć miarę trzeciego kąta, odejmując sumę dwóch znanych kątów od 180 stopni. * W trójkącie prostokątnym, jeden z kątów ma miarę 90 stopni. Zatem suma pozostałych dwóch kątów musi wynosić 90 stopni. Oznacza to, że kąty ostre w trójkącie prostokątnym są kątami dopełniającymi się (ich suma wynosi 90 stopni). * W trójkącie równobocznym, wszystkie trzy kąty są równe. Ponieważ ich suma wynosi 180 stopni, każdy kąt w trójkącie równobocznym ma miarę 60 stopni. * Zależności między kątami wewnętrznymi a zewnętrznymi: Kąt zewnętrzny trójkąta (kąt przyległy do kąta wewnętrznego) jest równy sumie miar dwóch kątów wewnętrznych nieprzyległych do niego.Te implikacje są kluczowe w rozwiązywaniu problemów geometrycznych i trygonometrycznych, a także w praktycznych zastosowaniach, o których powiemy w dalszej części.
Rodzaje trójkątów i ich kąty
Klasyfikacja trójkątów ze względu na miary kątów pozwala nam lepiej zrozumieć zależności między bokami i kątami:
* Trójkąt ostrokątny: Wszystkie trzy kąty są ostre (mniejsze niż 90 stopni). * Trójkąt prostokątny: Jeden kąt jest prosty (równy 90 stopni). * Trójkąt rozwartokątny: Jeden kąt jest rozwarty (większy niż 90 stopni).Zauważmy, że w trójkącie rozwartokątnym i prostokątnym nie może istnieć więcej niż jeden kąt rozwarty lub prosty, ponieważ suma miar wszystkich trzech kątów musi wynosić 180 stopni.
Wyjątki od reguły: Geometrie nieeuklidesowe
Warto zaznaczyć, że twierdzenie o sumie kątów w trójkącie jest prawdziwe tylko w geometrii euklidesowej, czyli w geometrii, której doświadczamy w naszym codziennym życiu. W geometriach nieeuklidesowych, takich jak geometria sferyczna czy geometria hiperboliczna, suma miar kątów w trójkącie może być różna od 180 stopni.
W geometrii sferycznej (np. na powierzchni kuli), suma miar kątów w trójkącie jest zawsze większa niż 180 stopni. Na przykład, możemy narysować trójkąt na powierzchni Ziemi, którego wierzchołki leżą na równiku i na biegunie północnym, z dwoma kątami prostymi na równiku. Trzeci kąt również będzie miał pewną miarę, więc suma kątów będzie większa niż 180 stopni.
W geometrii hiperbolicznej suma miar kątów w trójkącie jest zawsze mniejsza niż 180 stopni. Geometria hiperboliczna jest trudniejsza do wizualizacji, ale ma istotne zastosowania w fizyce i matematyce wyższej.
Real-world examples or data
Zasada, że suma kątów w trójkącie wynosi 180 stopni, ma szerokie zastosowanie w wielu dziedzinach:
* Architektura i budownictwo: Architekci i inżynierowie wykorzystują tę zasadę do projektowania stabilnych i wytrzymałych konstrukcji. Trójkąty są często używane jako elementy nośne w konstrukcjach budowlanych ze względu na ich sztywność i stabilność. Dokładne obliczanie kątów jest kluczowe dla zapewnienia bezpieczeństwa i funkcjonalności budynków. * Nawigacja: W nawigacji, szczególnie w nawigacji morskiej i lotniczej, trójkąty sferyczne (i związana z nimi trygonometria sferyczna) są używane do określania pozycji i kursu. Różnice w kątach wynikające z geometrii sferycznej muszą być uwzględniane podczas planowania długich tras. * Geodezja: Geodeci używają trójkątów i trygonometrii do pomiaru odległości i wysokości terenu. Twierdzenie o sumie kątów w trójkącie jest fundamentalne dla obliczeń triangulacyjnych. * Gry komputerowe i grafika 3D: Trójkąty są podstawowym elementem w modelowaniu 3D i renderingu grafiki komputerowej. Twierdzenie o sumie kątów jest używane do obliczania perspektywy i oświetlenia w scenach 3D. * Astronomia: Astronomowie używają trygonometrii, w tym wiedzy o trójkątach, do obliczania odległości do gwiazd i innych ciał niebieskich. Wykorzystują na przykład paralaksę trygonometryczną, która opiera się na pomiarze kątów i odległości w trójkącie utworzonym przez Ziemię, Słońce i odległą gwiazdę.Pomiary geodezyjne przy budowie mostów i tuneli również opierają się na precyzyjnych obliczeniach kątów, gdzie błędy mogą prowadzić do katastrofalnych konsekwencji. Samoloty wykorzystują triangulację do nawigacji i lądowania, gdzie dokładne pomiary kątowe są krytyczne dla bezpieczeństwa.
Conclusion or call to action
Twierdzenie o sumie miar kątów w trójkącie, choć wydaje się proste, jest jednym z najważniejszych twierdzeń w geometrii euklidesowej. Jego liczne zastosowania w różnych dziedzinach życia, od architektury po astronomię, świadczą o jego fundamentalnym znaczeniu. Zrozumienie tego twierdzenia i jego implikacji jest kluczowe dla każdego, kto interesuje się matematyką, naukami ścisłymi lub inżynierią.
Zachęcamy do dalszego zgłębiania wiedzy na temat geometrii, w tym innych własności trójkątów, czworokątów i innych figur geometrycznych. Spróbuj rozwiązywać zadania z geometrii, aby utrwalić swoją wiedzę i zrozumieć praktyczne zastosowania poznanych twierdzeń. Eksperymentuj z konstrukcjami geometrycznymi i obserwuj, jak te zasady znajdują odzwierciedlenie w otaczającym nas świecie. Matematyka jest wszędzie!