Suma Miar Kątów W Trapezie

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre konstrukcje geometryczne wydają się tak... harmonijne? Może to dlatego, że ukrywają w sobie proste, ale fundamentalne zasady. Jedną z nich jest suma miar kątów, a szczególnie intrygująca staje się, gdy dotyczy trapezu. Często traktujemy ją jako kolejny wzór do zapamiętania, ale zrozumienie jej korzeni pozwala na głębsze docenienie matematyki i jej zastosowań w otaczającym nas świecie. Ten artykuł rozwieje Twoje wątpliwości i pokaże, że geometria wcale nie musi być straszna!

Czym właściwie jest trapez?

Zacznijmy od podstaw. Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Te boki nazywamy podstawami trapezu. Pozostałe dwa boki, które nie są równoległe, to ramiona trapezu. Ważne jest, żeby pamiętać o słowie "przynajmniej" - równoległobok (w tym kwadrat i prostokąt) to również trapez, ale szczególnego rodzaju. Zrozumienie tej definicji jest kluczowe do dalszych rozważań o sumie kątów.

Trapez może być:

• Równoramienny: jeśli jego ramiona są równej długości.
• Prostokątny: jeśli jedno z jego ramion jest prostopadłe do podstaw.
• Różnoboczny: jeśli żaden z powyższych warunków nie jest spełniony.

Różne rodzaje trapezu wpływają na relacje między jego kątami, co zobaczymy w dalszej części artykułu.

Suma miar kątów w czworokącie – fundament wiedzy

Zanim przejdziemy konkretnie do trapezu, przypomnijmy sobie podstawową zasadę dotyczącą wszystkich czworokątów. Niezależnie od tego, czy mamy do czynienia z kwadratem, prostokątem, rombem, deltoidem, czy nieregularnym czworokątem, suma miar jego kątów wewnętrznych wynosi zawsze 360 stopni. To fundamentalna zasada geometrii euklidesowej, którą wykorzystamy w analizie trapezu.

Dowód tej zasady jest dość prosty. Możemy podzielić dowolny czworokąt na dwa trójkąty. Suma miar kątów w każdym trójkącie wynosi 180 stopni. Zatem suma miar kątów w dwóch trójkątach (czyli w całym czworokącie) wynosi 2 * 180 = 360 stopni. Proste, prawda?

Trapez i jego kąty – co musisz wiedzieć?

Wiemy już, że suma kątów w dowolnym czworokącie wynosi 360 stopni. W przypadku trapezu możemy jednak zaobserwować pewne dodatkowe zależności, wynikające z równoległości podstaw.

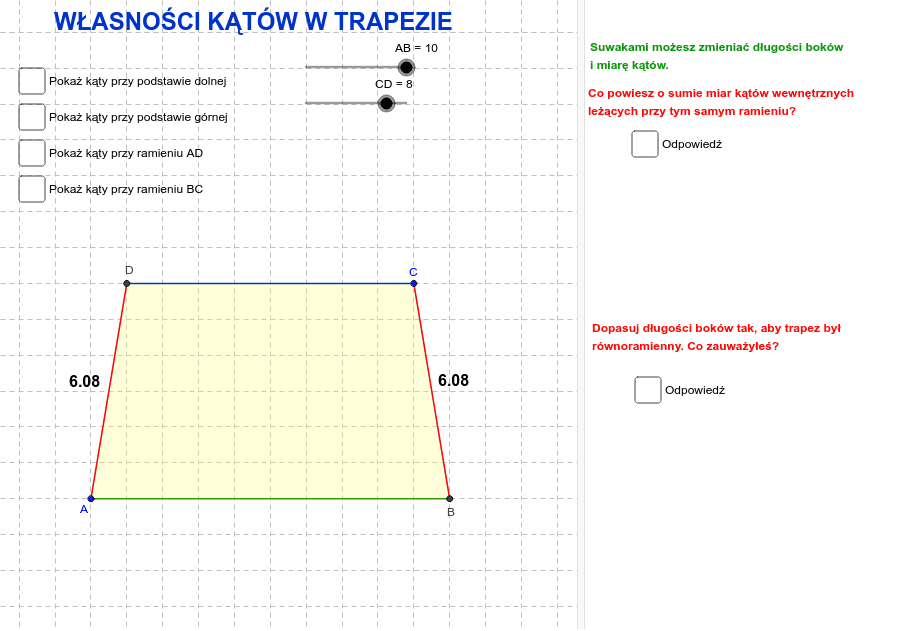
Kluczowa obserwacja: Kąty leżące przy tym samym ramieniu trapezu (a więc pomiędzy dwiema prostymi równoległymi - podstawami - przeciętymi trzecią prostą - ramieniem) są kątami przyległymi wewnętrznymi. A to oznacza, że ich suma wynosi 180 stopni!

Czyli, jeśli mamy trapez ABCD, gdzie AB i CD są podstawami (AB || CD), to:

• ∠A + ∠D = 180°
• ∠B + ∠C = 180°

To bardzo przydatna właściwość, która pozwala na rozwiązywanie wielu zadań z geometrii. Zamiast myśleć o czterech kątach naraz, możemy skupić się na parach kątów przyległych do ramion.

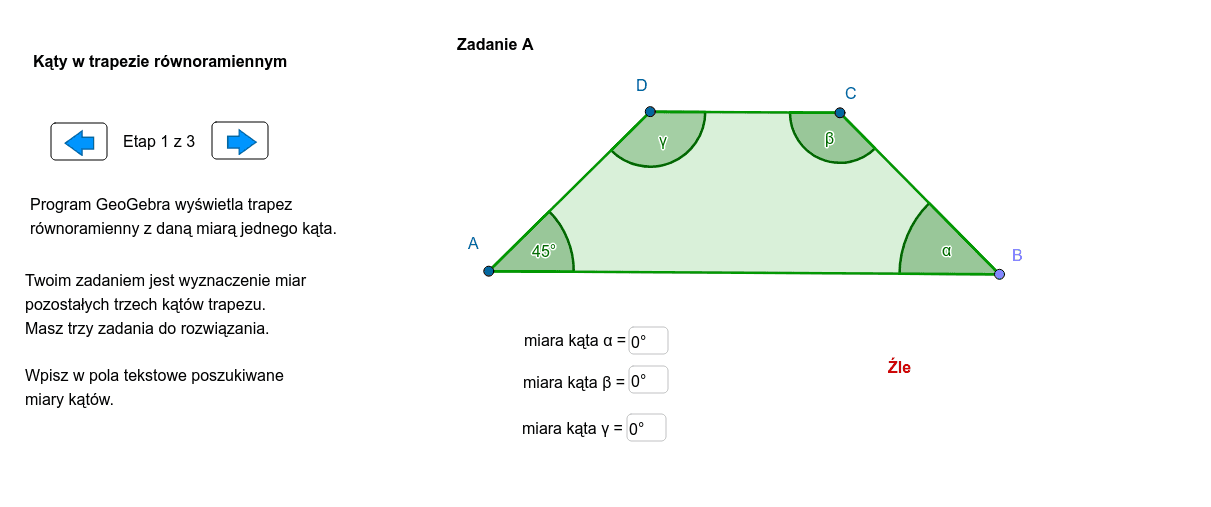
Trapez równoramienny – dodatkowe ułatwienie

Trapez równoramienny charakteryzuje się tym, że jego ramiona są równej długości. Ta cecha implikuje pewne dodatkowe zależności między kątami: kąty przy tej samej podstawie są równe.

W trapezie równoramiennym ABCD, gdzie AB i CD są podstawami (AB || CD) i AD = BC, mamy:

• ∠A = ∠B
• ∠C = ∠D

Dzięki temu, jeśli znamy miarę jednego z kątów przy podstawie, automatycznie znamy miarę drugiego. To znacznie upraszcza obliczenia!

Trapez prostokątny – jeszcze prościej!

Trapez prostokątny ma jedno z ramion prostopadłe do podstaw. Oznacza to, że dwa z jego kątów wewnętrznych są proste (mają miarę 90 stopni). W takim trapezie obliczenia stają się jeszcze łatwiejsze.

Załóżmy, że w trapezie prostokątnym ABCD, gdzie AB i CD są podstawami (AB || CD), bok AD jest prostopadły do podstaw. Wtedy:

• ∠A = 90°
• ∠D = 90°

Pozostaje nam obliczyć tylko miary kątów ∠B i ∠C, pamiętając, że ∠B + ∠C = 180°.

Praktyczne zastosowania – gdzie to się przydaje?

Może się wydawać, że wiedza o sumie miar kątów w trapezie jest tylko teoretyczna. Nic bardziej mylnego! Znajduje ona zastosowanie w wielu dziedzinach, takich jak:

• Architektura: Projektowanie dachów, mostów i innych konstrukcji.
• Inżynieria: Obliczanie obciążeń i stabilności konstrukcji.
• Geodezja: Wyznaczanie powierzchni działek i pomiary terenowe.
• Grafika komputerowa: Tworzenie trójwymiarowych modeli i animacji.

Wyobraź sobie architekta projektującego dach w kształcie trapezu. Musi on dokładnie obliczyć kąty nachylenia połaci, aby zapewnić odpowiednie odprowadzenie wody i śniegu. Znajomość zależności między kątami w trapezie jest tutaj niezbędna!

Jak zapamiętać te zasady?

Najlepszym sposobem na zapamiętanie zasad dotyczących sumy miar kątów w trapezie jest ćwiczenie! Rozwiąż jak najwięcej zadań, zaczynając od prostych, a stopniowo przechodząc do bardziej skomplikowanych. Rysuj trapezy, oznaczaj kąty i próbuj wyznaczać ich miary, korzystając z poznanych zależności.

Oto kilka wskazówek:

• Zacznij od definicji: Upewnij się, że rozumiesz, co to jest trapez i jakie są jego rodzaje.
• Pamiętaj o sumie kątów w czworokącie: To podstawa!
• Zwracaj uwagę na równoległość podstaw: To ona generuje zależności między kątami przyległymi do ramion.
• Wykorzystuj własności trapezu równoramiennego i prostokątnego: Upraszczają one obliczenia.
• Rysuj diagramy: Pomagają wizualizować problem i dostrzec zależności.

Przykładowe zadanie

Rozważmy trapez ABCD, w którym AB || CD. Wiemy, że ∠A = 70° i ∠B = 110°. Oblicz miary kątów ∠C i ∠D.

Rozwiązanie:

1. Korzystamy z faktu, że ∠A + ∠D = 180°. Zatem ∠D = 180° - ∠A = 180° - 70° = 110°.
2. Analogicznie, ∠B + ∠C = 180°. Zatem ∠C = 180° - ∠B = 180° - 110° = 70°.

Odpowiedź: ∠C = 70° i ∠D = 110°.

Podsumowanie

Mam nadzieję, że po przeczytaniu tego artykułu, suma miar kątów w trapezie nie będzie już dla Ciebie tajemnicą. Pamiętaj, że zrozumienie podstawowych zasad geometrii otwiera drzwi do rozwiązywania wielu praktycznych problemów. Nie bój się pytać, eksperymentować i ćwiczyć! Matematyka, wbrew pozorom, może być fascynująca!