Suma Miar Kątów W Równoległoboku

Czy kiedykolwiek zastanawiałeś się, dlaczego niektóre konstrukcje są tak stabilne, a inne nie? Często odpowiedź leży w geometrii, a konkretnie w kształtach takich jak równoległobok. Być może wydaje się to odległe od Twojego codziennego życia, ale zrozumienie sumy miar kątów w równoległoboku ma zaskakująco wiele praktycznych zastosowań. Jeśli kiedykolwiek miałeś trudności z zadaniami z geometrii, albo po prostu chcesz zrozumieć, jak działają otaczające Cię przedmioty, ten artykuł jest dla Ciebie.

Geometria może wydawać się abstrakcyjna, ale tak naprawdę jest wszędzie wokół nas. Od architektury budynków po projektowanie mebli, zasady geometrii odgrywają kluczową rolę. Równoległobok, jako jeden z podstawowych kształtów, jest obecny w wielu konstrukcjach i wzorach. Zrozumienie jego właściwości, w tym sumy miar jego kątów, pozwala nam lepiej analizować i projektować otaczający nas świat.

Dlaczego to w ogóle ważne?

Zanim przejdziemy do konkretnych obliczeń, warto zrozumieć, dlaczego w ogóle powinniśmy się tym zajmować. Zrozumienie geometrii równoległoboku pozwala:

• Projektować bardziej stabilne konstrukcje: Architekci i inżynierowie wykorzystują wiedzę o kątach w równoległobokach do projektowania budynków, mostów i innych konstrukcji, które są bardziej odporne na obciążenia.
• Rozwiązywać problemy praktyczne: Np. przy układaniu płytek, obliczaniu powierzchni, czy planowaniu przestrzeni.
• Rozwijać logiczne myślenie: Geometria uczy precyzji i logicznego dedukowania, co przydaje się w wielu dziedzinach życia.
• Zrozumieć działanie urządzeń: Wiele urządzeń, takich jak dźwignie, wykorzystuje zasady geometrii do efektywnego działania.

Czym właściwie jest Równoległobok?

Równoległobok to czworokąt (czyli figura geometryczna o czterech bokach) o następujących cechach:

• Przeciwległe boki są równoległe: Oznacza to, że nigdy się nie przetną, niezależnie od tego, jak daleko byśmy je przedłużyli.
• Przeciwległe boki są równe: Mają tę samą długość.
• Przeciwległe kąty są równe: Ich miary są identyczne.
• Suma wszystkich kątów wewnętrznych wynosi 360 stopni. To kluczowa informacja, którą rozwiniemy w dalszej części artykułu.

Suma Miar Kątów w Równoległoboku: Podstawy

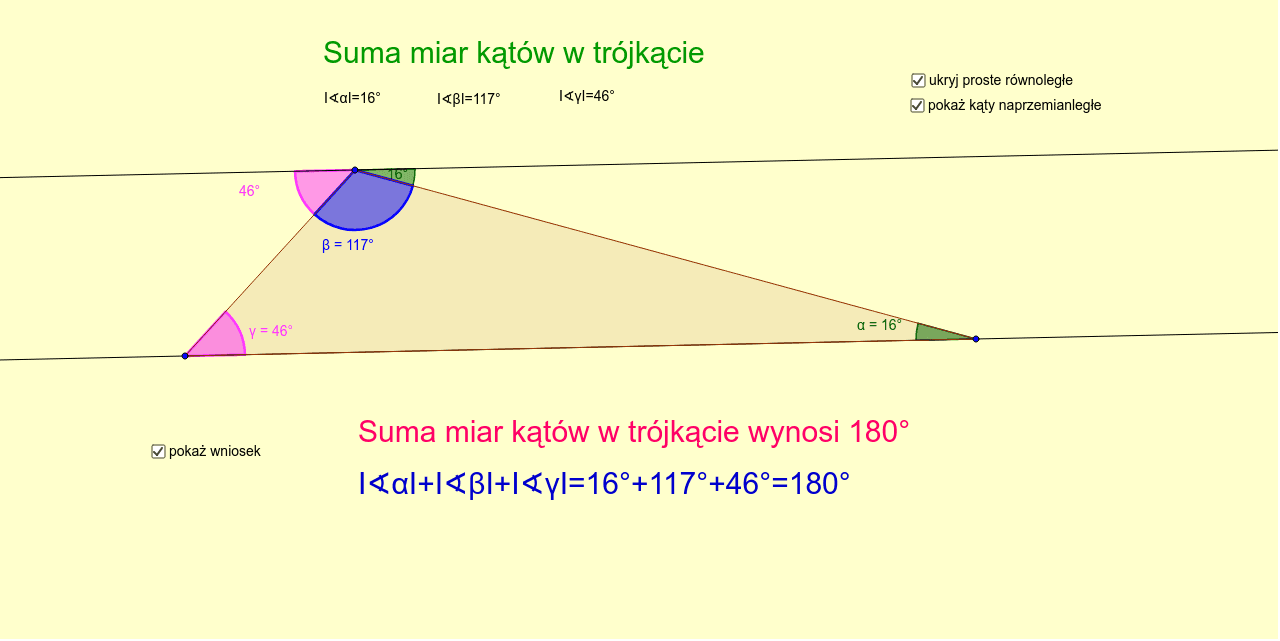
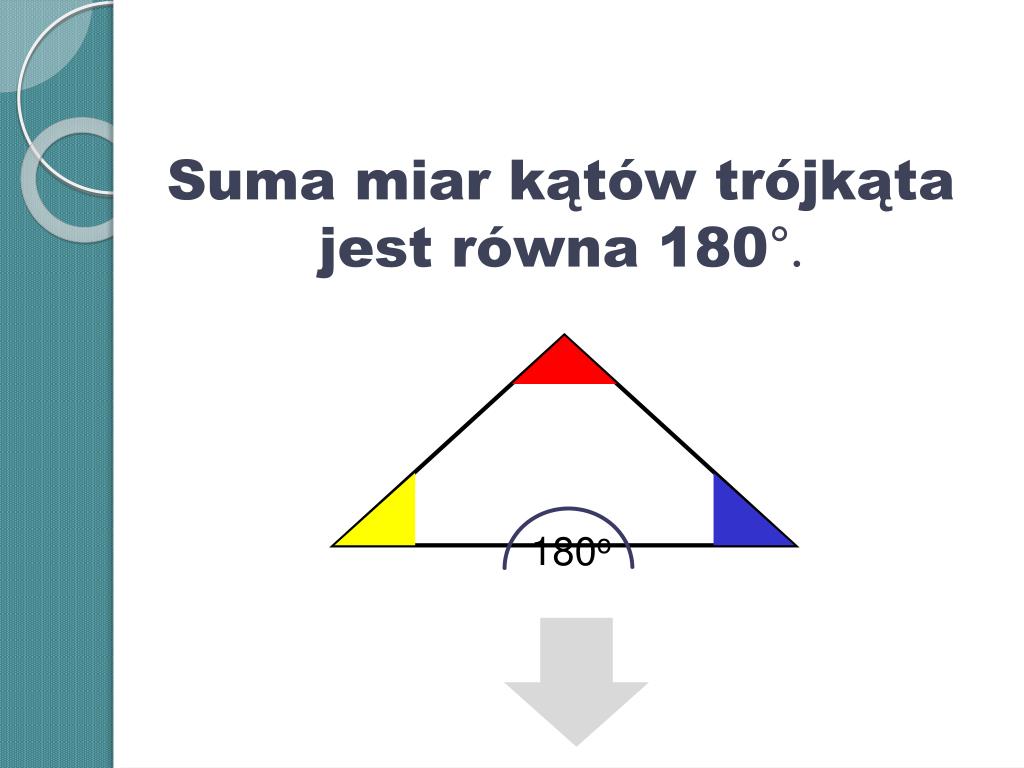
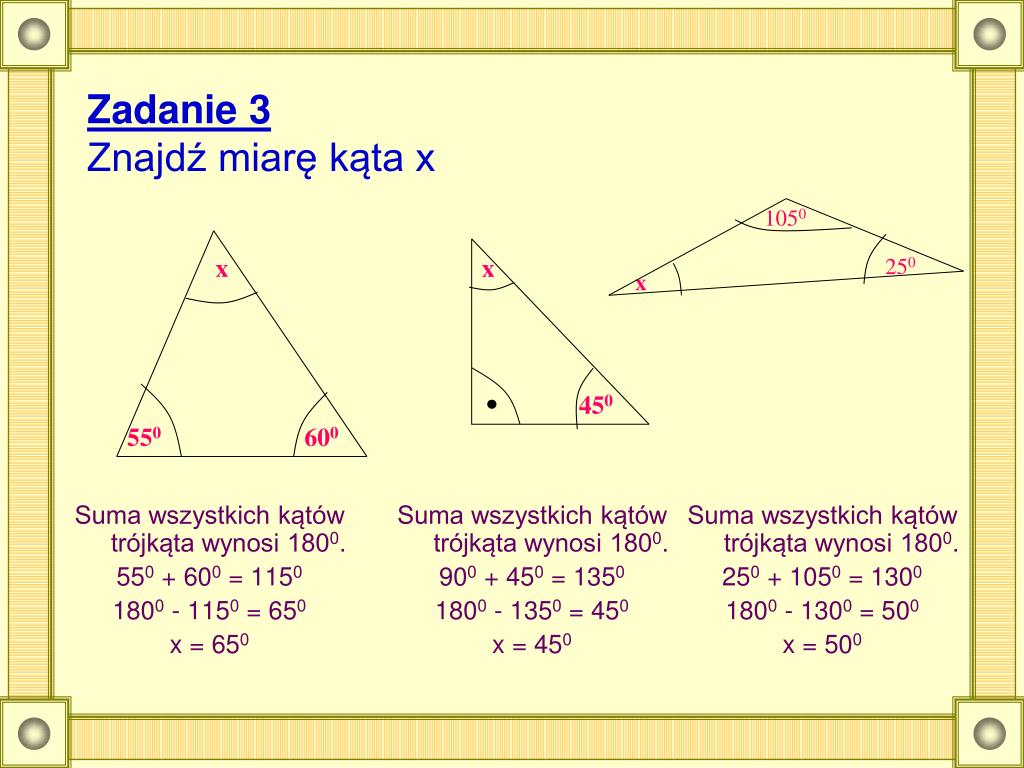
Kluczowa informacja, którą musimy zapamiętać, to fakt, że suma miar wszystkich kątów wewnętrznych w dowolnym czworokącie, w tym w równoległoboku, wynosi 360 stopni. Wynika to z prostego faktu, że każdy czworokąt można podzielić na dwa trójkąty, a suma kątów w każdym trójkącie wynosi 180 stopni (2 x 180 = 360).

W przypadku równoległoboku sytuacja jest o tyle prostsza, że jego przeciwległe kąty są równe. Oznacza to, że jeśli oznaczymy jeden z kątów jako α (alfa), a sąsiedni kąt jako β (beta), to możemy zapisać:

α + β + α + β = 360°

Upraszczając to równanie, otrzymujemy:

2α + 2β = 360°

Dzieląc obie strony przez 2, otrzymujemy:

α + β = 180°

Oznacza to, że suma dwóch sąsiednich kątów w równoległoboku wynosi 180 stopni. Są one kątami przyległymi.

Przykłady i Zastosowania

Załóżmy, że w równoległoboku jeden z kątów ma miarę 60 stopni. Jakie są miary pozostałych kątów?

1. Wiemy, że przeciwległy kąt również ma miarę 60 stopni.
2. Wiemy, że suma sąsiednich kątów wynosi 180 stopni. Zatem sąsiedni kąt ma miarę 180 - 60 = 120 stopni.
3. Przeciwległy do tego kąta również ma miarę 120 stopni.

W ten sposób obliczyliśmy miary wszystkich kątów w równoległoboku, znając miarę tylko jednego kąta. To pokazuje, jak potężne jest zrozumienie podstawowych zasad geometrii.

Praktyczne Zastosowania:

• Układanie płytek: Jeśli chcesz ułożyć płytki w kształcie równoległoboku, musisz znać kąty, aby prawidłowo je dopasować.
• Projektowanie mebli: Równoległoboki są często wykorzystywane w konstrukcjach mebli, takich jak stoliki czy krzesła. Zrozumienie kątów pozwala na optymalne rozłożenie obciążeń.
• Architektura: W architekturze równoległoboki mogą być wykorzystywane do tworzenia ciekawych efektów wizualnych, ale wymagają precyzyjnych obliczeń, aby zachować stabilność konstrukcji.

Kontrargumenty i Wyjątki

Niektórzy mogą argumentować, że wiedza o sumie kątów w równoległoboku jest zbędna, skoro w wielu sytuacjach możemy polegać na narzędziach pomiarowych. Owszem, możemy użyć kątomierza, ale zrozumienie dlaczego coś działa, daje nam znacznie większą kontrolę i pozwala na rozwiązywanie problemów w sytuacjach, gdy narzędzia są niedostępne lub niewystarczające. Ponadto, znajomość zasad geometrii rozwija logiczne myślenie i umiejętność rozwiązywania problemów, które przydają się w wielu dziedzinach życia.

Warto również wspomnieć o szczególnych przypadkach równoległoboków, takich jak prostokąt i kwadrat. W prostokącie wszystkie kąty są proste (90 stopni), więc suma dwóch sąsiednich kątów wynosi 90 + 90 = 180 stopni, co zgadza się z ogólną zasadą dla równoległoboków. Kwadrat to szczególny przypadek prostokąta, gdzie wszystkie boki są równe. Zatem suma kątów w tych figurach również wynosi 360 stopni.

Podsumowanie i Dalsze Kroki

Zrozumienie sumy miar kątów w równoległoboku to podstawa geometrii, która ma szerokie zastosowanie w życiu codziennym. Od projektowania budynków po układanie płytek, wiedza ta pozwala nam lepiej rozumieć i kształtować otaczający nas świat. Pamiętaj, że suma wszystkich kątów wewnętrznych w równoległoboku wynosi 360 stopni, a suma dwóch sąsiednich kątów wynosi 180 stopni. Znając miarę jednego kąta, możesz z łatwością obliczyć miary pozostałych kątów.

Co możesz zrobić dalej?

• Rozwiąż więcej zadań: Ćwiczenie czyni mistrza! Poszukaj zadań z geometrii związanych z równoległobokami i spróbuj je rozwiązać.
• Poszukaj równoległoboków w swoim otoczeniu: Zwróć uwagę na architekturę budynków, meble, wzory na dywanach. Zobacz, gdzie możesz dostrzec równoległoboki.
• Zgłębiaj wiedzę: Poszukaj informacji o innych figurach geometrycznych i ich właściwościach.

Mamy nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć sumę miar kątów w równoległoboku. Czy teraz, patrząc na otaczający Cię świat, zauważasz więcej równoległoboków niż wcześniej?